Surface types
From Serpent Wiki
Contents
Elementary surfaces
Notes:
- Elementary surfaces refer here to surfaces that can be represented by a single equation.
Planes
Notes:
- Parametric form of the general plane is assumed if four values are provided in the surface card. With six values the plane is assumed to be defined by three points.
- The positive side for a plane defined by three points is determined by the order in which the points are entered (see the right-hand rule).
| Surface name | Parameters | Surface equation | Description |
|---|---|---|---|
| px | x0 | 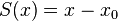
|
Plane perpendicular to x-axis at x = x0 |
| py | y0 | 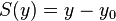
|
Plane perpendicular to y-axis at y = y0 |
| pz | z0 | 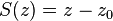
|
Plane perpendicular to z-axis at z = z0 |
| plane | A, B, C, D | 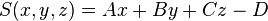
|
General plane in parametric form |
| plane | x1, y1, z1, x2, y2, z2, x3, y3, z3 | General plane defined by three points |
Second-order quadratic surfaces
Notes:
- cyl is the same surface as cylz
- Infinite cylinder is assumed if three values are provided in the surface card for cylx, cyly, cylz or cyl. With five values the surface is assumed to be a truncated cylinder.
| Surface name | Parameters | Surface equation | Description |
|---|---|---|---|
| cylx | y0, z0, r | 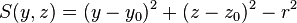
|
Infinite cylinder parallel to x-axis, centred at (y0,z0), radius r |
| cyly | x0, z0, r | 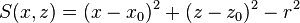
|
Infinite cylinder parallel to y-axis, centred at (x0,z0), radius r |
| cylz, cyl | x0, y0, r | 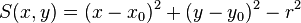
|
Infinite cylinder parallel to z-axis, centred at (x0,y0), radius r |
| cylv | x0, y0, z0, u0, v0, w0, r | 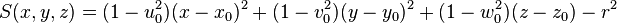
|
Infinite cylinder, parallel to (u0,v0,w0), centred at (x0,y0,z0), radius r |
| sph | x0, y0, z0, r | 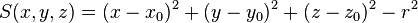
|
Sphere, centred at (x0,y0,z0), radius r |
| cone | x0, y0, z0, r, h | 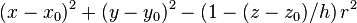
|
Half cone parallel to z-axis, base at (x0,y0,z0), base radius r, height h (distance from base to vertex) |
| quadratic | A, B, C, D, E, F, G, H, I, J | 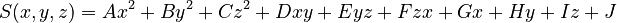
|
General quadratic surface in parametric form |
Non-quadratic surfaces
Notes:
- Serpent can currently handle only circular torii. Radii R1 and R2 must be set equal (denoted in the surface equations as R).
| Surface name | Parameters | Surface equation | Description | Notes |
|---|---|---|---|---|
| inf | - | 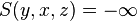
|
All space | Can not be used in root universe |
| torx | x0, y0, z0, r, R1, R2 | 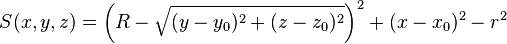
|
Circular torus with major radius R perpendicular to x-axis, centred at (x0, y0, z0), minor radius r | |
| tory | x0, y0, z0, r, R1, R2 | 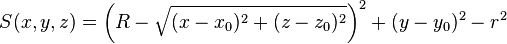
|
Circular torus with major radius R perpendicular to y-axis, centred at (x0, y0, z0), minor radius r | |
| torz | x0, y0, z0, r, R1, R2 | 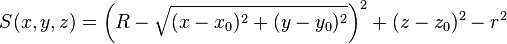
|
Circular torus with major radius R perpendicular to z-axis, centred at (x0, y0, z0), minor radius r |
Derived surface types
Notes:
- Derived surfaces refer here to surfaces composed of two or more elementary types.
Truncated cylinders
Notes:
- Truncated cylinders use the same names as the infinite cylinders above.
- Infinite cylinder is assumed if three values are provided in the surface card for cylx, cyly, cylz or cyl. With five values the surface is assumed to be a truncated cylinder.
| Surface name | Parameters | Composed of | Description |
|---|---|---|---|
| cylx | y0, z0, r, x0, x1 | Infinite cylinder + two planes | Infinite cylinder parallel to x-axis, centred at (y0,z0), radius r, truncated between [x0, x1] |
| cyly | x0, z0, r, y0, y1 | Infinite cylinder + two planes | Infinite cylinder parallel to y-axis, centred at (x0,z0), radius r, truncated between [y0, y1] |
| cylz, cyl | x0, y0, r, z0, z1 | Infinite cylinder + two planes | Infinite cylinder parallel to z-axis, centred at (x0,y0), radius r, truncated between [z0, z1] |
Regular prisms
Notes:
- All prisms are parallel to z-axis, and they can be rotated using surface transformations.
- Infinite and truncated triangular prisms use the same name, and are composed by three or five planes, respectively. Infinite prism is assumed if three/four values are provided in the surface card tric. With six values the surface is assumed to be a truncated (equilateral) triangular prism.
- Triangular prisms orientation, ori, corresponds to the cardinal direction of the non-aligned vertex of the triangle. Default orientation is North. It follows the scheme: W-S-E-N (W=1, S=2, E=3, N=4).
| Surface name | Parameters | Composed of | Description |
|---|---|---|---|
| tric | x0, y0, r, ori | three planes | Infinite (equilateral) triangular prism parallel to z-axis, centred at (x0,y0), incircle radius r, orientation ori (optional) |
| x0, y0, r, ori, z0, z1 | five planes | Truncated (equilateral) triangular prism parallel to z-axis, centred at (x0,y0), incircle radius r, orientation ori, truncated between [z0, z1] | |
| sqc | x0, y0, d | four planes | Infinite square prism parallel to z-axis, centred at (x0,y0), half-width d |
| rect | x0, x1, y0, y1 | four planes | Infinite rectangular prism parallel to z-axis, between [x0, x1] and [y0, y1] |
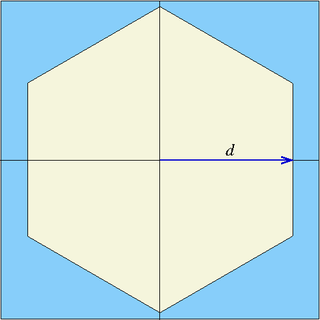
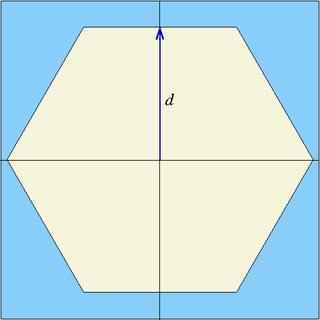
| hexxc | x0, y0, d | six planes | Infinite hexagonal prism parallel to z-axis, centred at (x0,y0), flat surface perpendicular to x-axis, half-width d |
| hexyc | x0, y0, d | six planes | Infinite hexagonal prism parallel to z-axis, centred at (x0,y0), flat surface perpendicular to y-axis, half-width d |
| hexxprism | x0, y0, d, z0, z1 | eight planes | Truncated hexagonal prism parallel to z-axis, centred at (x0,y0), flat surface perpendicular to x-axis, half-width d, truncated between [z0, z1] |
| hexyprism | x0, y0, d, z0, z1 | eight planes | Truncated hexagonal prism parallel to z-axis, centred at (x0,y0), flat surface perpendicular to y-axis, half-width d, truncated between [z0, z1] |
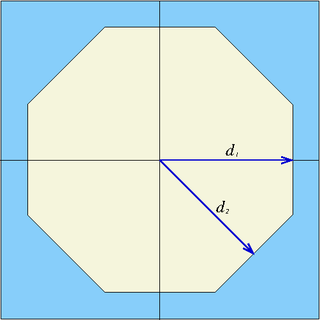
| octa | x0, y0, d1, d2 | eight planes | Infinite octagonal prism parallel to z-axis, centred at (x0,y0), half-widths d1 and d2 |
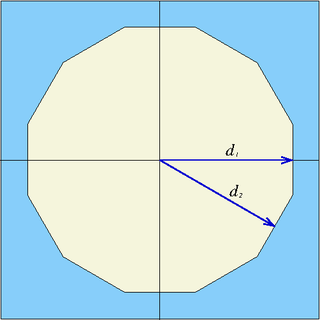
| dode | x0, y0, d1, d2 | twelve planes | Infinite dodecagonal prism parallel to z-axis, centred at (x0,y0), half-widths d1 and d2 |
3D polyhedra
Notes:
- The description of parallelepiped may be wrong.
| Surface name | Parameters | Composed of | Description |
|---|---|---|---|
| cube | x0, y0, z0, d | six planes | Cube, centred at (x0,y0,z0), half-width d |
| cuboid | x0, x1, y0, y1, z0, z1 | six planes | Cuboid, between [x0, x1], [y0, y1] and [z0, z1] |
| ppd | x0, y0, z0, Lx, Ly, Lz,  x, x, 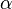 y, y, 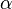 z z
|
six planes | Parallelepiped, with corner at (x0, y0, z0) and edges of length Lx, Ly and Lz at angles 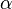 x, x, 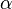 y and y and 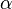 z (in degrees) with respect to the coordinate axes z (in degrees) with respect to the coordinate axes
|
Other derived surface types
| Surface name | Parameters | Description |
|---|---|---|
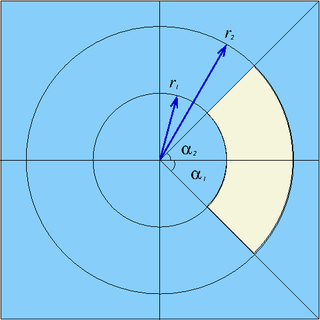
| pad | x0, y0, r1, r2, 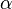 1, 1, 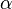 2 2
|
Sector from 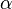 1 to 1 to 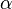 2 (in degrees) of a cylinder parallel to z-axis, centred at (x0,y0), between radii r1 and r2 2 (in degrees) of a cylinder parallel to z-axis, centred at (x0,y0), between radii r1 and r2
|
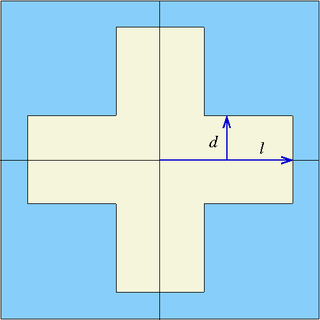
| cross | x0, y0, l, d | Cruciform prism parallel to z-axis, centered at (x0,y0), half-width l, half-thickness d |
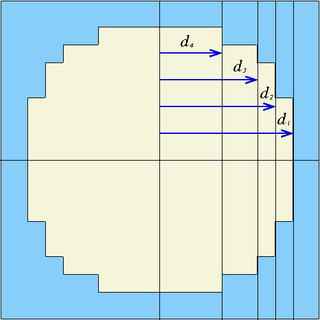
| gcross | x0, y0, d1, d2, ... | Prism parallel to z-axis, centred at (x0,y0), formed by planes at distances dn from the center ("generalized cruciform prism", see figure below) |
| hexxap | x0, y0, wd, dw, a | Surface for simplified modeling of hexagonal fuel assembly angle pieces. Consists of two infinite hexagonal prisms parallel to z-axis, centered at (x0, y0), flat surfaces perpendicular to x-axis, with the outer hexagon having outer half-width of wd, and the surface perpendicular thickness is dw (the inner hexagon half width is wd - dw), and each half-section of each angle piece with width of a, measured from the tip of the angle piece angle to the flat surface of the angle piece. |
| hexyap | x0, y0, wd, dw, a | Surface for simplified modeling of hexagonal fuel assembly angle pieces. Consists of two infinite hexagonal prisms parallel to z-axis, centered at (x0, y0), flat surfaces perpendicular to y-axis, with the outer hexagon having outer half-width of wd, and the surface perpendicular thickness is dw (the inner hexagon half width is wd - dw), and each half-section of each angle piece with width of a, measured from the tip of the angle piece angle to the flat surface of the angle piece. |
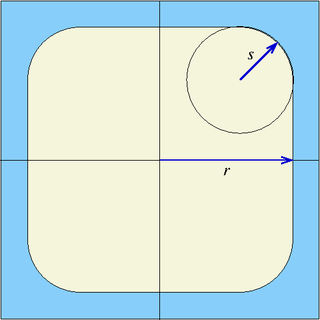
Rounded corners
Infinite prisms:
- sqc
- hexxc
- hexyc
- cross
Allow defining rounded corners. The radius is then provided as the last surface parameter (s in figure below):
MCNP-equivalent surfaces
Notes:
- Additional surfaces included to simplify input conversion between Serpent and MCNP.
- For description, see Chapter 3 of the MCNP5 User's Guide.[1]
| Surface name | Equivalent surface in MCNP |
|---|---|
| box | BOX |
| ckx | K/X |
| cky | K/Y |
| ckz | K/Z |
| mplane | P (form defined by three points) |
| rcc | RCC |
| x | X |
| y | Y |
| z | Z |
User-defined surfaces
Notes:
- Remember to make a backup of your subroutine before installing new updates.
- If you have a working surface routine that might be useful for other users as well, contact the Serpent team and we'll include it in the next update as a built-in type.
| Surface name | Parameters | Description |
|---|---|---|
| usr | p1, p2, ... | User-defined surface, implemented in source file "usersurf.c". The subroutine receives the number and list of surface parameters as input. Instructions are included as comments in the source file. |
References
- ^ X-5 Monte Carlo Team. "MCNP — A General Monte Carlo N-Particle Transport Code, Version 5, Volume II: User’s Guide." LA-CP-03-0245, Los Alamos National Laboratory, 2003.