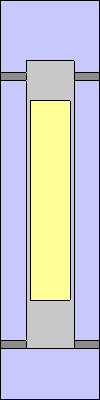
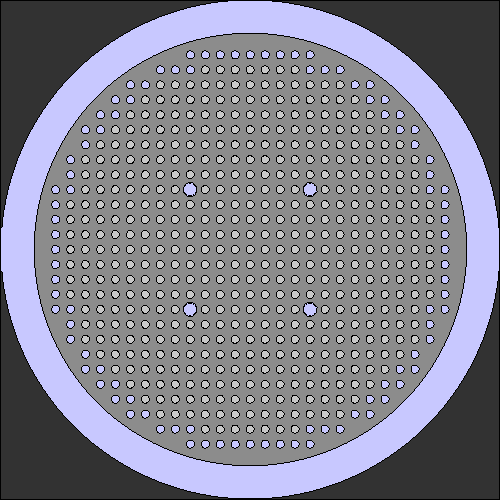
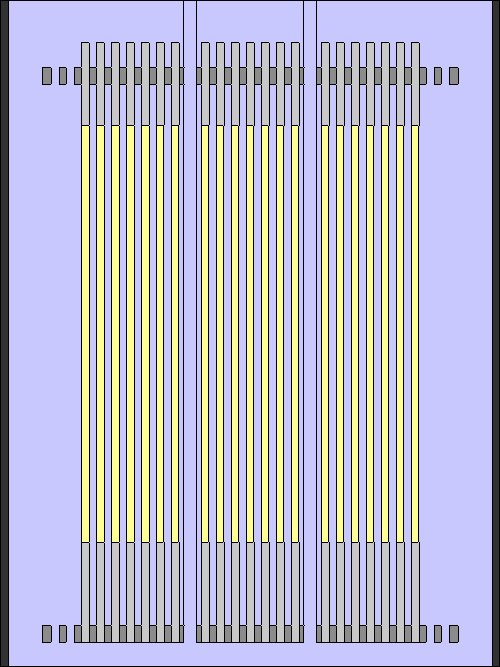
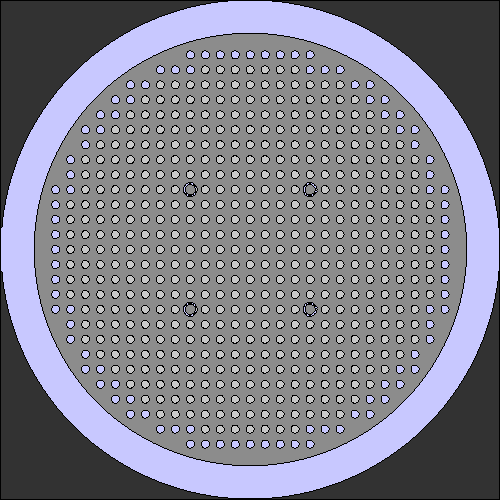
Tutorial

This page contains the beginnings of a hands-on tutorial in Serpent that will walk you through the use of simple pin-cell and assembly geometry models for reactor physics simulations. The tutorial culminates on building a 3D geometry model for a small research reactor.

1 Prerequisite
2 Part 1: Infinite homogeneous system
3 Part 2: A 2D pin-cell (infinite lattice)
4 Part 3: A 2D assembly model (infinite lattice)
5 Part 4: Assembly burnup calculation
6 Part 5: A 3D research reactor model
7 Part 6: Generating a set of group constants for a fuel assembly
8 Final part: Options for real life calculations
9 References

Prerequisite

A compiled version of Serpent 2. This tutorial assumes that you have compiled Serpent with OpenMP parallelization and the graphics libraries. I

This tutorial assumes that you can run Serpent 2 simply by typing sss2 in your terminal, i.e. you either have the executable in your PATH or have created an alias for the executable. If this is not the case, you'll need to replace the sss2 run-commands with the full path to your executable.

Cross section, decay data (.dec) and neutron induced fission yield (.nfy) libraries.

This tutorial assumes that you have defined a default cross section directory file for Serpent using the SERPENT_ACELIB environment variable (see the notes of set acelib). If this is not the case, you'll need to give the path to a cross section directory file in the input using set acelib.

OCTAVE is used for analyzing and plotting some of the results from the calculations. The analysis scripts may be executable also with MATLAB. You can also create your own analysis scripts using, e.g. Python and simply use the scripts provided here as example. Alternatively, the serpentTools python package can be used to process output files without the need for custom parsers.

Part 1: Infinite homogeneous system

Part 1 overview

The first model in this tutorial is the simplest geometry model one can imagine: an infinite homogeneous system consisting of a single material. Here the infinite material is 4.0 wt-% enriched uranium with a density of 10.1 g/cm³.

We will use the infinite homogeneous system example for three tasks:

Finding the critical enrichment of an infinite uranium system.
Tallying the neutron energy spectrum in the critical infinite uranium system.
Testing the effect of added neutron moderation on the multiplication factor and energy spectrum of the system.

Part 1 input

The input of the model is shown below and consists of only six definitions:

Defining the single material, which is called fuel in this example.
Defining the geometry by
1. Defining a boundary surface for our geometry which separates our model to the inside and outside of the geometry.
2. Defining two geometry cells: One containing the material fuel and the other being defined as an outside cell.
3. Applying a reflective boundary condition at the geometry outer boundary to make the system infinite.
Setting up any other run parameters, here simply setting the neutron population that is to be simulated.

Copy and paste the input below to a file named infinite on your computer.

Colors in the input correspond to:

Comments: These are ignored by Serpent.
Control words: A constantly updating list of control words can be found in the Input syntax manual. Everything between two control words that is not a comment is treated as a parameter to the first control word.
Name definitions: Name definitions for the various Serpent objects can contain characters and numbers and are used for referencing certain objects in other definitions.
Name references: References to named objects defined in the input. Name references can be made even if the name definition has not been made yet as long as the name will be defined later in the input.

Input for infinite homogeneous model

% --- Very simple infinite homogeneous geometry for Serpent tutorial

/************************
 * Material definitions *
 ************************/

% --- Fuel material (4.0 wt-% enriched uranium), density 10.1 g/cm3

mat fuel     -10.1
92235.03c    -0.04 
92238.03c    -0.96

/************************
 * Geometry definitions *
 ************************/

% --- Bounding surface for the geometry is an axially infinite square prism
%     centered at 0.0 0.0 with a half-width of 100 cm
%     see: https://serpent.vtt.fi/mediawiki/index.php/Surface_types

surf s1 sqc 0.0 0.0 100.0

% --- Cell c1 belongs to the base universe 0, contains the material fuel
%     and covers everything inside surface s1

cell c1 0 fuel      -s1

% --- Cell c2 belongs to the base universe 0, is defined as an "outside" cell
%     and covers everything outside surface s1

cell c2 0 outside    s1

% --- Use reflective boundary conditions to make the system infinite
%     These are applied on the boundary surface of the outside cell
%     i.e. surface s1

set bc 2
 
/******************
 * Run parameters *
 ******************/

% --- Neutron population: 5000 neutrons per cycle, 100 active / 20 inactive cycles

set pop 5000 100 20

Running the input for the infinite system

Simply run the input from terminal, by being in the same directory as the input-file and executing

sss2 infinite

If you compiled Serpent with OpenMP libraries for parallel computing, you can run the input with multiple OpenMP threads to use more than one processor:

sss2 -omp N infinite

where N is the number of OpenMP threads you want to use and can be set to, e.g. the number of available processor cores.

An example of the expected output is given below, although you should note that the statistical nature of the Monte Carlo methods means that you will not get exactly same values for the k-effective:

Expected output for the infinite system

  _                   .-=-.           .-=-.          .-==-.       
 { }      __        .' O o '.       .' O o '.       /  -<' )--<   
 { }    .' O'.     / o .-. O \     / o .-. O \     /  .---`       
 { }   / .-. o\   /O  /   \  o\   /O  /   \  o\   /O /            
  \ `-` /   \ O`-'o  /     \  O`-'o  /     \  O`-`o /             
   `-.-`     '.____.'       `._____.'       `.____.'              

Serpent 2 beta

A Continuous-energy Monte Carlo Reactor Physics Burnup Calculation Code

 - Version 2.1.29 (June 12, 2017) -- Contact: serpent@vtt.fi

 - Reference: J. Leppanen, et al. "The Serpent Monte Carlo code: Status,
              development and applications in 2013." Ann. Nucl. Energy,
              82 (2015) 142-150.

 - Compiled Jun 19 2017 10:21:15

 - MPI Parallel calculation mode not available

 - OpenMP Parallel calculation mode available

 - Geometry and mesh plotting available

 - Default data path set to: "/home/vvvillehe/XSdata/"

Begin calculation on Mon Sep 11 12:51:14 2017

Reading input file "infinite"...

Checking duplicate input definitions...
OK.

Creating geometry...
OK.

Counting geometry zones...

Processing cells...
OK.

Linking materials to geometry...
OK.

Counting cells...
OK.

Processing data for group constant generation:

 - 70 energy groups in micro-group structure
 - 2 energy groups in macro-group structure
 - B1 fundamental mode calculation is not run
 - Group constants generated in 1 universes
 - Discontinuity factors are not calculated
 - Pin-power distributions are not calculated
 - Albedos are not calculated
 - Poison cross sections are not calculated

Reading ACE directory files...
OK.

Adding nuclides in material fuel...

Nuclide  92235.03c -- uranium 235 at 300K (U-235)
Nuclide  92238.03c -- uranium 238 at 300K (U-238)

Checking data and printing output...
OK.


***** Mon Sep 11 12:51:15 2017 (seed = 1505123474)
Warning message from function ProcessNuclides:

Minimum photon cross section energy 1.000000E+37 MeV is
above the energy grid minimum 1.000000E-03 MeV.
The energy grid minimum is set to 1.000000E+37 MeV.
Possible changes in energy cutoff cards (warned if any).


***** Mon Sep 11 12:51:15 2017 (seed = 1505123474)
Warning message from function ProcessNuclides:

Photon energy cutoff 1.000000E-03 MeV is changed to 1.000000E+37.


Generating unionize energy grids...

Adding points:

 92235.03c -- Points added in neutron grid: 30884
 92238.03c -- Points added in neutron grid: 64918

Generating unionized energy grid:

 - Unionization performed without grid thinning
   between 1.00E-11 and 20.0 MeV.

 - Final neutron grid size: 95836 points.

 - 2.12 Mb of memory allocated for grid data

OK.

Processing cross sections and ENDF reaction laws...

Nuclide  92235.03c -- uranium 235 at 300K (U-235)
Nuclide  92238.03c -- uranium 238 at 300K (U-238)

SUMMARY -- 2 nuclides included in calculation:

 - 2 transport nuclides
 - Neutron energy cut-offs at 1.00E-11 and 20.0 MeV
 - 88 transport reactions
 - 2 special reactions
 - 18.07 Mb of memory allocated for data

Normalizing compositions and processing mixtures...
OK.

Allocating memory for macroscopic cross section data...
OK.

Allocating memory for particle structures...
OK.

Calculating maximum densities...
OK.

Performing density cut-off...
OK.

Sorting material-wise reaction lists:

   0% complete
 100% complete

Calculating macroscopic cross sections:

   0% complete
 100% complete

Calculating DT neutron majorant cross section:

   0% complete
 100% complete

Clearing results and statistics...
OK.

Sampling initial source...
OK.

Inactive cycle   1 /  20: k-eff = 1.00000
Inactive cycle   2 /  20: k-eff = 0.83420
Inactive cycle   3 /  20: k-eff = 0.79549
Inactive cycle   4 /  20: k-eff = 0.87011
Inactive cycle   5 /  20: k-eff = 0.81582
Inactive cycle   6 /  20: k-eff = 0.83654
Inactive cycle   7 /  20: k-eff = 0.81429
Inactive cycle   8 /  20: k-eff = 0.88334
Inactive cycle   9 /  20: k-eff = 0.84641
Inactive cycle  10 /  20: k-eff = 0.88078
Inactive cycle  11 /  20: k-eff = 0.82141
Inactive cycle  12 /  20: k-eff = 0.83916
Inactive cycle  13 /  20: k-eff = 0.85225
Inactive cycle  14 /  20: k-eff = 0.84424
Inactive cycle  15 /  20: k-eff = 0.82836
Inactive cycle  16 /  20: k-eff = 0.80235
Inactive cycle  17 /  20: k-eff = 0.84424
Inactive cycle  18 /  20: k-eff = 0.85251
Inactive cycle  19 /  20: k-eff = 0.81653
Inactive cycle  20 /  20: k-eff = 0.83237

----- Begin active cycles -----

------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle    1 / 100  Source neutrons :  5177

Running time :                  0:00:09
Estimated running time :        -:--:--
Estimated running time left :   -:--:--

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.86184 +/- 0.00000  [0.86184  0.86184]
k-eff (implicit)  = 0.84234 +/- 0.00000  [0.84234  0.84234]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle    2 / 100  Source neutrons :  4873

Running time :                  0:00:09
Estimated running time :        -:--:--
Estimated running time left :   -:--:--

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.85090 +/- 0.01095  [0.82944  0.87235]
k-eff (implicit)  = 0.83921 +/- 0.00313  [0.83308  0.84535]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle    3 / 100  Source neutrons :  4979

Running time :                  0:00:10
Estimated running time :        -:--:--
Estimated running time left :   -:--:--

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.84607 +/- 0.00795  [0.83049  0.86165]
k-eff (implicit)  = 0.83824 +/- 0.00205  [0.83421  0.84226]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle    4 / 100  Source neutrons :  4980

Running time :                  0:00:10
Estimated running time :        -:--:--
Estimated running time left :   -:--:--

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84282 +/- 0.00649  [0.83010  0.85555]
k-eff (implicit)  = 0.83595 +/- 0.00271  [0.83063  0.84127]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle    5 / 100  Source neutrons :  5072

Running time :                  0:00:11
Estimated running time :        0:00:57
Estimated running time left :   0:00:46

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.84327 +/- 0.00505  [0.83338  0.85317]
k-eff (implicit)  = 0.83419 +/- 0.00274  [0.82882  0.83956]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle    6 / 100  Source neutrons :  4895

Running time :                  0:00:11
Estimated running time :        0:00:57
Estimated running time left :   0:00:45

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84061 +/- 0.00491  [0.83100  0.85023]
k-eff (implicit)  = 0.83488 +/- 0.00234  [0.83029  0.83946]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle    7 / 100  Source neutrons :  5060

Running time :                  0:00:12
Estimated running time :        0:00:57
Estimated running time left :   0:00:45

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.84013 +/- 0.00417  [0.83195  0.84831]
k-eff (implicit)  = 0.83563 +/- 0.00212  [0.83149  0.83978]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle    8 / 100  Source neutrons :  5034

Running time :                  0:00:12
Estimated running time :        0:00:57
Estimated running time left :   0:00:44

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.84049 +/- 0.00363  [0.83337  0.84760]
k-eff (implicit)  = 0.83605 +/- 0.00188  [0.83237  0.83974]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle    9 / 100  Source neutrons :  5141

Running time :                  0:00:12
Estimated running time :        0:00:56
Estimated running time left :   0:00:43

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84340 +/- 0.00433  [0.83491  0.85189]
k-eff (implicit)  = 0.83678 +/- 0.00181  [0.83323  0.84032]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   10 / 100  Source neutrons :  4689

Running time :                  0:00:13
Estimated running time :        0:00:56
Estimated running time left :   0:00:43

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84034 +/- 0.00494  [0.83067  0.85002]
k-eff (implicit)  = 0.83686 +/- 0.00162  [0.83368  0.84003]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   11 / 100  Source neutrons :  5340

Running time :                  0:00:13
Estimated running time :        0:00:56
Estimated running time left :   0:00:42

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84286 +/- 0.00513  [0.83281  0.85291]
k-eff (implicit)  = 0.83725 +/- 0.00152  [0.83428  0.84022]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   12 / 100  Source neutrons :  4906

Running time :                  0:00:14
Estimated running time :        0:00:56
Estimated running time left :   0:00:42

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.84360 +/- 0.00474  [0.83432  0.85289]
k-eff (implicit)  = 0.83862 +/- 0.00195  [0.83480  0.84243]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   13 / 100  Source neutrons :  5000

Running time :                  0:00:14
Estimated running time :        0:00:56
Estimated running time left :   0:00:41

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84423 +/- 0.00440  [0.83560  0.85286]
k-eff (implicit)  = 0.83770 +/- 0.00201  [0.83376  0.84164]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   14 / 100  Source neutrons :  4759

Running time :                  0:00:15
Estimated running time :        0:00:56
Estimated running time left :   0:00:41

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.84184 +/- 0.00473  [0.83257  0.85111]
k-eff (implicit)  = 0.83771 +/- 0.00186  [0.83406  0.84135]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   15 / 100  Source neutrons :  5270

Running time :                  0:00:15
Estimated running time :        0:00:56
Estimated running time left :   0:00:40

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84268 +/- 0.00448  [0.83390  0.85147]
k-eff (implicit)  = 0.83771 +/- 0.00173  [0.83432  0.84111]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   16 / 100  Source neutrons :  4903

Running time :                  0:00:16
Estimated running time :        0:00:56
Estimated running time left :   0:00:40

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.84238 +/- 0.00420  [0.83414  0.85062]
k-eff (implicit)  = 0.83794 +/- 0.00164  [0.83474  0.84115]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   17 / 100  Source neutrons :  5066

Running time :                  0:00:16
Estimated running time :        0:00:56
Estimated running time left :   0:00:39

Estimated relative CPU usage :   100.2%

k-eff (analog)    = 0.84277 +/- 0.00397  [0.83499  0.85054]
k-eff (implicit)  = 0.83708 +/- 0.00176  [0.83363  0.84054]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   18 / 100  Source neutrons :  4864

Running time :                  0:00:17
Estimated running time :        0:00:56
Estimated running time left :   0:00:39

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.84183 +/- 0.00386  [0.83427  0.84939]
k-eff (implicit)  = 0.83702 +/- 0.00166  [0.83376  0.84028]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   19 / 100  Source neutrons :  5195

Running time :                  0:00:17
Estimated running time :        0:00:56
Estimated running time left :   0:00:38

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84269 +/- 0.00375  [0.83534  0.85003]
k-eff (implicit)  = 0.83771 +/- 0.00172  [0.83435  0.84107]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   20 / 100  Source neutrons :  4758

Running time :                  0:00:18
Estimated running time :        0:00:56
Estimated running time left :   0:00:38

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.84138 +/- 0.00379  [0.83396  0.84880]
k-eff (implicit)  = 0.83786 +/- 0.00163  [0.83465  0.84106]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   21 / 100  Source neutrons :  5296

Running time :                  0:00:18
Estimated running time :        0:00:56
Estimated running time left :   0:00:37

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.84250 +/- 0.00377  [0.83511  0.84989]
k-eff (implicit)  = 0.83784 +/- 0.00155  [0.83480  0.84089]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   22 / 100  Source neutrons :  4817

Running time :                  0:00:19
Estimated running time :        0:00:56
Estimated running time left :   0:00:37

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84208 +/- 0.00362  [0.83498  0.84918]
k-eff (implicit)  = 0.83827 +/- 0.00154  [0.83525  0.84130]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   23 / 100  Source neutrons :  5027

Running time :                  0:00:19
Estimated running time :        0:00:56
Estimated running time left :   0:00:36

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84189 +/- 0.00347  [0.83510  0.84868]
k-eff (implicit)  = 0.83835 +/- 0.00148  [0.83545  0.84124]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   24 / 100  Source neutrons :  4986

Running time :                  0:00:20
Estimated running time :        0:00:56
Estimated running time left :   0:00:36

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.84162 +/- 0.00333  [0.83509  0.84814]
k-eff (implicit)  = 0.83830 +/- 0.00141  [0.83553  0.84107]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   25 / 100  Source neutrons :  5009

Running time :                  0:00:20
Estimated running time :        0:00:56
Estimated running time left :   0:00:35

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.84143 +/- 0.00320  [0.83516  0.84770]
k-eff (implicit)  = 0.83851 +/- 0.00137  [0.83582  0.84120]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   26 / 100  Source neutrons :  5049

Running time :                  0:00:21
Estimated running time :        0:00:56
Estimated running time left :   0:00:35

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.84157 +/- 0.00308  [0.83554  0.84760]
k-eff (implicit)  = 0.83871 +/- 0.00133  [0.83609  0.84132]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   27 / 100  Source neutrons :  5140

Running time :                  0:00:21
Estimated running time :        0:00:56
Estimated running time left :   0:00:35

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.84258 +/- 0.00313  [0.83645  0.84871]
k-eff (implicit)  = 0.83871 +/- 0.00128  [0.83620  0.84123]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   28 / 100  Source neutrons :  4907

Running time :                  0:00:22
Estimated running time :        0:00:56
Estimated running time left :   0:00:34

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.84294 +/- 0.00303  [0.83699  0.84888]
k-eff (implicit)  = 0.83878 +/- 0.00124  [0.83635  0.84120]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   29 / 100  Source neutrons :  4885

Running time :                  0:00:22
Estimated running time :        0:00:57
Estimated running time left :   0:00:34

Estimated relative CPU usage :    99.8%

k-eff (analog)    = 0.84259 +/- 0.00295  [0.83681  0.84837]
k-eff (implicit)  = 0.83902 +/- 0.00122  [0.83663  0.84140]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   30 / 100  Source neutrons :  5101

Running time :                  0:00:23
Estimated running time :        0:00:57
Estimated running time left :   0:00:33

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.84283 +/- 0.00286  [0.83723  0.84843]
k-eff (implicit)  = 0.83909 +/- 0.00118  [0.83678  0.84140]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   31 / 100  Source neutrons :  4844

Running time :                  0:00:23
Estimated running time :        0:00:56
Estimated running time left :   0:00:33

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84220 +/- 0.00284  [0.83665  0.84776]
k-eff (implicit)  = 0.83927 +/- 0.00115  [0.83700  0.84153]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   32 / 100  Source neutrons :  5069

Running time :                  0:00:24
Estimated running time :        0:00:56
Estimated running time left :   0:00:32

Estimated relative CPU usage :   100.2%

k-eff (analog)    = 0.84197 +/- 0.00276  [0.83657  0.84737]
k-eff (implicit)  = 0.83902 +/- 0.00114  [0.83678  0.84126]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   33 / 100  Source neutrons :  5146

Running time :                  0:00:24
Estimated running time :        0:00:57
Estimated running time left :   0:00:32

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.84248 +/- 0.00272  [0.83715  0.84782]
k-eff (implicit)  = 0.83844 +/- 0.00125  [0.83598  0.84089]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   34 / 100  Source neutrons :  4777

Running time :                  0:00:25
Estimated running time :        0:00:57
Estimated running time left :   0:00:32

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84184 +/- 0.00272  [0.83652  0.84717]
k-eff (implicit)  = 0.83807 +/- 0.00127  [0.83558  0.84056]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   35 / 100  Source neutrons :  5022

Running time :                  0:00:25
Estimated running time :        0:00:57
Estimated running time left :   0:00:31

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84134 +/- 0.00268  [0.83608  0.84660]
k-eff (implicit)  = 0.83781 +/- 0.00126  [0.83534  0.84028]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   36 / 100  Source neutrons :  4947

Running time :                  0:00:26
Estimated running time :        0:00:57
Estimated running time left :   0:00:31

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84063 +/- 0.00270  [0.83533  0.84593]
k-eff (implicit)  = 0.83794 +/- 0.00123  [0.83553  0.84035]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   37 / 100  Source neutrons :  5137

Running time :                  0:00:26
Estimated running time :        0:00:57
Estimated running time left :   0:00:30

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.84056 +/- 0.00263  [0.83540  0.84571]
k-eff (implicit)  = 0.83793 +/- 0.00120  [0.83559  0.84028]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   38 / 100  Source neutrons :  5042

Running time :                  0:00:27
Estimated running time :        0:00:57
Estimated running time left :   0:00:30

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84067 +/- 0.00256  [0.83565  0.84570]
k-eff (implicit)  = 0.83794 +/- 0.00117  [0.83566  0.84023]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   39 / 100  Source neutrons :  5086

Running time :                  0:00:27
Estimated running time :        0:00:57
Estimated running time left :   0:00:29

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84116 +/- 0.00254  [0.83617  0.84614]
k-eff (implicit)  = 0.83800 +/- 0.00114  [0.83577  0.84022]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   40 / 100  Source neutrons :  4784

Running time :                  0:00:28
Estimated running time :        0:00:57
Estimated running time left :   0:00:29

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84069 +/- 0.00252  [0.83574  0.84563]
k-eff (implicit)  = 0.83796 +/- 0.00111  [0.83579  0.84013]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   41 / 100  Source neutrons :  5005

Running time :                  0:00:28
Estimated running time :        0:00:57
Estimated running time left :   0:00:28

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.84026 +/- 0.00250  [0.83537  0.84516]
k-eff (implicit)  = 0.83810 +/- 0.00109  [0.83597  0.84024]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   42 / 100  Source neutrons :  5001

Running time :                  0:00:29
Estimated running time :        0:00:57
Estimated running time left :   0:00:28

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83986 +/- 0.00247  [0.83502  0.84470]
k-eff (implicit)  = 0.83831 +/- 0.00108  [0.83619  0.84044]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   43 / 100  Source neutrons :  4897

Running time :                  0:00:29
Estimated running time :        0:00:57
Estimated running time left :   0:00:27

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.83908 +/- 0.00253  [0.83411  0.84405]
k-eff (implicit)  = 0.83816 +/- 0.00107  [0.83606  0.84025]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   44 / 100  Source neutrons :  5279

Running time :                  0:00:29
Estimated running time :        0:00:57
Estimated running time left :   0:00:27

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83936 +/- 0.00249  [0.83448  0.84424]
k-eff (implicit)  = 0.83805 +/- 0.00105  [0.83599  0.84011]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   45 / 100  Source neutrons :  4871

Running time :                  0:00:30
Estimated running time :        0:00:57
Estimated running time left :   0:00:26

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83914 +/- 0.00245  [0.83435  0.84393]
k-eff (implicit)  = 0.83832 +/- 0.00106  [0.83624  0.84041]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   46 / 100  Source neutrons :  5106

Running time :                  0:00:30
Estimated running time :        0:00:57
Estimated running time left :   0:00:26

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.83931 +/- 0.00240  [0.83461  0.84401]
k-eff (implicit)  = 0.83830 +/- 0.00104  [0.83626  0.84034]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   47 / 100  Source neutrons :  4952

Running time :                  0:00:31
Estimated running time :        0:00:57
Estimated running time left :   0:00:25

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83930 +/- 0.00235  [0.83470  0.84390]
k-eff (implicit)  = 0.83833 +/- 0.00102  [0.83634  0.84033]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   48 / 100  Source neutrons :  5081

Running time :                  0:00:31
Estimated running time :        0:00:57
Estimated running time left :   0:00:25

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83958 +/- 0.00231  [0.83504  0.84411]
k-eff (implicit)  = 0.83828 +/- 0.00100  [0.83632  0.84023]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   49 / 100  Source neutrons :  4830

Running time :                  0:00:32
Estimated running time :        0:00:56
Estimated running time left :   0:00:24

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83925 +/- 0.00229  [0.83476  0.84374]
k-eff (implicit)  = 0.83831 +/- 0.00098  [0.83640  0.84023]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   50 / 100  Source neutrons :  5171

Running time :                  0:00:32
Estimated running time :        0:00:56
Estimated running time left :   0:00:24

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83950 +/- 0.00226  [0.83507  0.84392]
k-eff (implicit)  = 0.83848 +/- 0.00097  [0.83657  0.84038]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   51 / 100  Source neutrons :  4947

Running time :                  0:00:33
Estimated running time :        0:00:56
Estimated running time left :   0:00:23

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83956 +/- 0.00221  [0.83522  0.84390]
k-eff (implicit)  = 0.83843 +/- 0.00095  [0.83656  0.84030]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   52 / 100  Source neutrons :  4832

Running time :                  0:00:33
Estimated running time :        0:00:56
Estimated running time left :   0:00:23

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.83907 +/- 0.00222  [0.83472  0.84343]
k-eff (implicit)  = 0.83841 +/- 0.00094  [0.83658  0.84025]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   53 / 100  Source neutrons :  5104

Running time :                  0:00:34
Estimated running time :        0:00:56
Estimated running time left :   0:00:22

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83893 +/- 0.00219  [0.83464  0.84321]
k-eff (implicit)  = 0.83842 +/- 0.00092  [0.83662  0.84022]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   54 / 100  Source neutrons :  4947

Running time :                  0:00:34
Estimated running time :        0:00:56
Estimated running time left :   0:00:22

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83862 +/- 0.00217  [0.83437  0.84287]
k-eff (implicit)  = 0.83824 +/- 0.00092  [0.83644  0.84004]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   55 / 100  Source neutrons :  5038

Running time :                  0:00:35
Estimated running time :        0:00:56
Estimated running time left :   0:00:21

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83844 +/- 0.00213  [0.83426  0.84263]
k-eff (implicit)  = 0.83817 +/- 0.00091  [0.83640  0.83995]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   56 / 100  Source neutrons :  5084

Running time :                  0:00:35
Estimated running time :        0:00:56
Estimated running time left :   0:00:21

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83852 +/- 0.00210  [0.83440  0.84263]
k-eff (implicit)  = 0.83809 +/- 0.00089  [0.83634  0.83984]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   57 / 100  Source neutrons :  4909

Running time :                  0:00:36
Estimated running time :        0:00:56
Estimated running time left :   0:00:20

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.83832 +/- 0.00207  [0.83426  0.84238]
k-eff (implicit)  = 0.83820 +/- 0.00088  [0.83647  0.83993]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   58 / 100  Source neutrons :  4951

Running time :                  0:00:36
Estimated running time :        0:00:56
Estimated running time left :   0:00:20

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83799 +/- 0.00206  [0.83395  0.84203]
k-eff (implicit)  = 0.83813 +/- 0.00087  [0.83642  0.83984]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   59 / 100  Source neutrons :  5098

Running time :                  0:00:37
Estimated running time :        0:00:56
Estimated running time left :   0:00:19

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83794 +/- 0.00203  [0.83397  0.84191]
k-eff (implicit)  = 0.83818 +/- 0.00086  [0.83650  0.83986]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   60 / 100  Source neutrons :  4836

Running time :                  0:00:37
Estimated running time :        0:00:56
Estimated running time left :   0:00:19

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.83744 +/- 0.00205  [0.83341  0.84147]
k-eff (implicit)  = 0.83792 +/- 0.00088  [0.83619  0.83965]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   61 / 100  Source neutrons :  5255

Running time :                  0:00:38
Estimated running time :        0:00:56
Estimated running time left :   0:00:18

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83763 +/- 0.00203  [0.83365  0.84161]
k-eff (implicit)  = 0.83793 +/- 0.00087  [0.83623  0.83963]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   62 / 100  Source neutrons :  4846

Running time :                  0:00:38
Estimated running time :        0:00:56
Estimated running time left :   0:00:18

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83739 +/- 0.00201  [0.83345  0.84133]
k-eff (implicit)  = 0.83783 +/- 0.00086  [0.83614  0.83951]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   63 / 100  Source neutrons :  5153

Running time :                  0:00:39
Estimated running time :        0:00:56
Estimated running time left :   0:00:17

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.83756 +/- 0.00199  [0.83367  0.84145]
k-eff (implicit)  = 0.83787 +/- 0.00085  [0.83621  0.83953]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   64 / 100  Source neutrons :  4940

Running time :                  0:00:39
Estimated running time :        0:00:56
Estimated running time left :   0:00:17

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83757 +/- 0.00195  [0.83374  0.84140]
k-eff (implicit)  = 0.83778 +/- 0.00084  [0.83614  0.83942]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   65 / 100  Source neutrons :  5114

Running time :                  0:00:40
Estimated running time :        0:00:56
Estimated running time left :   0:00:16

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83787 +/- 0.00195  [0.83405  0.84168]
k-eff (implicit)  = 0.83770 +/- 0.00083  [0.83607  0.83932]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   66 / 100  Source neutrons :  4874

Running time :                  0:00:40
Estimated running time :        0:00:56
Estimated running time left :   0:00:16

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83783 +/- 0.00192  [0.83407  0.84159]
k-eff (implicit)  = 0.83762 +/- 0.00082  [0.83601  0.83923]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   67 / 100  Source neutrons :  5093

Running time :                  0:00:41
Estimated running time :        0:00:57
Estimated running time left :   0:00:15

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83802 +/- 0.00190  [0.83430  0.84175]
k-eff (implicit)  = 0.83742 +/- 0.00083  [0.83579  0.83906]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   68 / 100  Source neutrons :  4720

Running time :                  0:00:41
Estimated running time :        0:00:57
Estimated running time left :   0:00:15

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83751 +/- 0.00194  [0.83371  0.84131]
k-eff (implicit)  = 0.83748 +/- 0.00082  [0.83587  0.83909]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   69 / 100  Source neutrons :  5186

Running time :                  0:00:42
Estimated running time :        0:00:57
Estimated running time left :   0:00:15

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83745 +/- 0.00191  [0.83370  0.84120]
k-eff (implicit)  = 0.83738 +/- 0.00082  [0.83578  0.83898]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   70 / 100  Source neutrons :  4945

Running time :                  0:00:42
Estimated running time :        0:00:57
Estimated running time left :   0:00:14

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.83726 +/- 0.00189  [0.83355  0.84097]
k-eff (implicit)  = 0.83733 +/- 0.00081  [0.83575  0.83891]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   71 / 100  Source neutrons :  5134

Running time :                  0:00:43
Estimated running time :        0:00:57
Estimated running time left :   0:00:14

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83738 +/- 0.00187  [0.83372  0.84105]
k-eff (implicit)  = 0.83724 +/- 0.00080  [0.83567  0.83880]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   72 / 100  Source neutrons :  4762

Running time :                  0:00:43
Estimated running time :        0:00:57
Estimated running time left :   0:00:13

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83694 +/- 0.00190  [0.83323  0.84066]
k-eff (implicit)  = 0.83734 +/- 0.00080  [0.83578  0.83890]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   73 / 100  Source neutrons :  5208

Running time :                  0:00:44
Estimated running time :        0:00:57
Estimated running time left :   0:00:13

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83698 +/- 0.00187  [0.83331  0.84064]
k-eff (implicit)  = 0.83739 +/- 0.00079  [0.83585  0.83893]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   74 / 100  Source neutrons :  5074

Running time :                  0:00:44
Estimated running time :        0:00:57
Estimated running time left :   0:00:12

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.83718 +/- 0.00186  [0.83354  0.84081]
k-eff (implicit)  = 0.83727 +/- 0.00078  [0.83573  0.83880]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   75 / 100  Source neutrons :  4814

Running time :                  0:00:45
Estimated running time :        0:00:57
Estimated running time left :   0:00:12

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.83695 +/- 0.00185  [0.83333  0.84057]
k-eff (implicit)  = 0.83721 +/- 0.00078  [0.83569  0.83873]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   76 / 100  Source neutrons :  5117

Running time :                  0:00:45
Estimated running time :        0:00:57
Estimated running time left :   0:00:11

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83698 +/- 0.00182  [0.83341  0.84055]
k-eff (implicit)  = 0.83719 +/- 0.00077  [0.83568  0.83869]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   77 / 100  Source neutrons :  4981

Running time :                  0:00:46
Estimated running time :        0:00:57
Estimated running time left :   0:00:11

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83697 +/- 0.00180  [0.83345  0.84049]
k-eff (implicit)  = 0.83715 +/- 0.00076  [0.83566  0.83863]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   78 / 100  Source neutrons :  4892

Running time :                  0:00:46
Estimated running time :        0:00:57
Estimated running time left :   0:00:10

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83672 +/- 0.00179  [0.83322  0.84023]
k-eff (implicit)  = 0.83720 +/- 0.00075  [0.83573  0.83867]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   79 / 100  Source neutrons :  5267

Running time :                  0:00:47
Estimated running time :        0:00:57
Estimated running time left :   0:00:10

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83704 +/- 0.00180  [0.83352  0.84056]
k-eff (implicit)  = 0.83719 +/- 0.00074  [0.83574  0.83864]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   80 / 100  Source neutrons :  4790

Running time :                  0:00:47
Estimated running time :        0:00:57
Estimated running time left :   0:00:09

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83690 +/- 0.00178  [0.83341  0.84038]
k-eff (implicit)  = 0.83720 +/- 0.00073  [0.83577  0.83863]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   81 / 100  Source neutrons :  4876

Running time :                  0:00:48
Estimated running time :        0:00:57
Estimated running time left :   0:00:09

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.83650 +/- 0.00180  [0.83297  0.84003]
k-eff (implicit)  = 0.83721 +/- 0.00072  [0.83580  0.83863]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   82 / 100  Source neutrons :  5004

Running time :                  0:00:48
Estimated running time :        0:00:57
Estimated running time left :   0:00:08

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83613 +/- 0.00182  [0.83256  0.83969]
k-eff (implicit)  = 0.83721 +/- 0.00071  [0.83581  0.83860]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   83 / 100  Source neutrons :  5153

Running time :                  0:00:49
Estimated running time :        0:00:57
Estimated running time left :   0:00:08

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83606 +/- 0.00180  [0.83254  0.83958]
k-eff (implicit)  = 0.83719 +/- 0.00070  [0.83581  0.83857]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   84 / 100  Source neutrons :  5087

Running time :                  0:00:49
Estimated running time :        0:00:57
Estimated running time left :   0:00:07

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83616 +/- 0.00178  [0.83268  0.83965]
k-eff (implicit)  = 0.83711 +/- 0.00070  [0.83574  0.83849]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   85 / 100  Source neutrons :  4976

Running time :                  0:00:50
Estimated running time :        0:00:57
Estimated running time left :   0:00:07

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83621 +/- 0.00176  [0.83277  0.83966]
k-eff (implicit)  = 0.83705 +/- 0.00069  [0.83568  0.83841]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   86 / 100  Source neutrons :  5022

Running time :                  0:00:50
Estimated running time :        0:00:57
Estimated running time left :   0:00:06

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83631 +/- 0.00174  [0.83290  0.83972]
k-eff (implicit)  = 0.83700 +/- 0.00069  [0.83566  0.83835]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   87 / 100  Source neutrons :  4868

Running time :                  0:00:50
Estimated running time :        0:00:57
Estimated running time left :   0:00:06

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83615 +/- 0.00173  [0.83276  0.83953]
k-eff (implicit)  = 0.83710 +/- 0.00069  [0.83575  0.83844]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   88 / 100  Source neutrons :  5084

Running time :                  0:00:51
Estimated running time :        0:00:57
Estimated running time left :   0:00:05

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.83614 +/- 0.00171  [0.83280  0.83949]
k-eff (implicit)  = 0.83703 +/- 0.00068  [0.83569  0.83837]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   89 / 100  Source neutrons :  5052

Running time :                  0:00:51
Estimated running time :        0:00:57
Estimated running time left :   0:00:05

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83624 +/- 0.00169  [0.83292  0.83956]
k-eff (implicit)  = 0.83708 +/- 0.00068  [0.83576  0.83841]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   90 / 100  Source neutrons :  4906

Running time :                  0:00:52
Estimated running time :        0:00:57
Estimated running time left :   0:00:04

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83616 +/- 0.00167  [0.83287  0.83944]
k-eff (implicit)  = 0.83696 +/- 0.00068  [0.83563  0.83829]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   91 / 100  Source neutrons :  5034

Running time :                  0:00:52
Estimated running time :        0:00:57
Estimated running time left :   0:00:04

Estimated relative CPU usage :   100.1%

k-eff (analog)    = 0.83614 +/- 0.00166  [0.83289  0.83938]
k-eff (implicit)  = 0.83691 +/- 0.00067  [0.83559  0.83823]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   92 / 100  Source neutrons :  5017

Running time :                  0:00:53
Estimated running time :        0:00:57
Estimated running time left :   0:00:03

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83615 +/- 0.00164  [0.83294  0.83936]
k-eff (implicit)  = 0.83703 +/- 0.00068  [0.83570  0.83835]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   93 / 100  Source neutrons :  5118

Running time :                  0:00:54
Estimated running time :        0:00:57
Estimated running time left :   0:00:03

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83637 +/- 0.00164  [0.83317  0.83958]
k-eff (implicit)  = 0.83698 +/- 0.00067  [0.83566  0.83829]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   94 / 100  Source neutrons :  4978

Running time :                  0:00:54
Estimated running time :        0:00:57
Estimated running time left :   0:00:02

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83655 +/- 0.00163  [0.83336  0.83974]
k-eff (implicit)  = 0.83702 +/- 0.00066  [0.83572  0.83832]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   95 / 100  Source neutrons :  4931

Running time :                  0:00:55
Estimated running time :        0:00:57
Estimated running time left :   0:00:02

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83660 +/- 0.00161  [0.83344  0.83976]
k-eff (implicit)  = 0.83698 +/- 0.00066  [0.83569  0.83827]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   96 / 100  Source neutrons :  4796

Running time :                  0:00:55
Estimated running time :        0:00:57
Estimated running time left :   0:00:01

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83630 +/- 0.00162  [0.83311  0.83948]
k-eff (implicit)  = 0.83709 +/- 0.00066  [0.83579  0.83838]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   97 / 100  Source neutrons :  5254

Running time :                  0:00:55
Estimated running time :        0:00:57
Estimated running time left :   0:00:01

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83642 +/- 0.00161  [0.83326  0.83958]
k-eff (implicit)  = 0.83700 +/- 0.00066  [0.83570  0.83829]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   98 / 100  Source neutrons :  5044

Running time :                  0:00:56
Estimated running time :        0:00:57
Estimated running time left :   0:00:00

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83661 +/- 0.00161  [0.83346  0.83977]
k-eff (implicit)  = 0.83691 +/- 0.00066  [0.83562  0.83820]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle   99 / 100  Source neutrons :  4931

Running time :                  0:00:56
Estimated running time :        0:00:57
Estimated running time left :   0:00:00

Estimated relative CPU usage :    99.9%

k-eff (analog)    = 0.83669 +/- 0.00159  [0.83356  0.83981]
k-eff (implicit)  = 0.83689 +/- 0.00065  [0.83561  0.83817]

(O4) (OMP=1) 
------------------------------------------------------------
------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle  100 / 100  Source neutrons :  4981

Running time :                  0:00:57
Estimated running time :        0:00:57
Estimated running time left :   0:00:00

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83673 +/- 0.00158  [0.83363  0.83982]
k-eff (implicit)  = 0.83705 +/- 0.00067  [0.83575  0.83836]

(O4) (OMP=1) 
------------------------------------------------------------

Transport cycle completed in 56.3 seconds.

The output of a simple Serpent simulation can be divided to the pre-processing part and the neutron transport part. The pre-processing part consists of reading the input-files and processing the material, geometry and cross section data, whereas the neutron transport part consists of first executing the inactive cycles, followed by the execution of the active cycles.

The results are only collected during the active cycles. The inactive cycles are used to allow the fission source to converge from the initial guess to its fundamental mode before the collection of the results is begun. If too few inactive cycles are used, the collected results do not represent the fundamental mode and will be incorrect. One of the traditional methods for estimating the required number of inactive cycles is to monitor the Shannon entropy of the fission source as a function of the cycle number (see set his).

Running the input will also produce multiple output files, the full description of which can be found here. The main output file infinite_res.m contains many result variables calculated from the simulation and can be executed with MATLAB or OCTAVE to automatically bring the variables in as workspace variables.

Finding the critical uranium enrichment

For the next part of the tutorial we will use the same input-file as previously (the infinite file). You can try to find out the critical enrichment for the fuel material by modifying the material definition. Let's look at the fuel material definition (in the input file) a bit closer:

% --- Fuel material (4.0 wt-% enriched uranium), density 10.1 g/cm3

mat fuel     -10.1
92235.03c    -0.04 
92238.03c    -0.96

The first line of the material definition contains the command word mat which tells Serpent that a material definition will follow. The name of the material is set to fuel and the density of the material is set to -10.1, where the negative number tells Serpent that it should be interpreted as mass density (a positive number would indicate atomic density). The unit of mass density (see the list of units) used in Serpent is g/cm³. The initial material definition line is followed by the material composition:

92235.03c    -0.04 
92238.03c    -0.96

Here the value on the left is the nuclide id (which must correspond to an entry in the cross section directory file) and the value on the right is its mass fraction (negative number) or atomic fraction (positive number) in the composition. The nuclide ids consist of three parts:

92235.03c    -0.04 
92238.03c    -0.96

The first one or two numbers are the atomic number of the nuclide.
The following three numbers give the mass number of the nuclide.
The last three characters after a period/dot give the library identifier of the nuclide. The library identifier typically represents the temperature of the nuclide (and in some cases the cross section library).

In our case, the atomic number of both nuclides in the composition is 92 indicating that the nuclides are uranium. The mass numbers of the two nuclides are 235 and 238 further identifying the nuclides as ²³⁵U and ²³⁸U. The library identifier 03c indicates that those variants of the ²³⁵U and ²³⁸U cross section libraries that are in the temperature of 300 K should be used.

The mass fractions given in the material definition mean that the material consists of 0.04 parts (in mass) of ²³⁵U and 0.96 parts (in mass) of ²³⁸U. This equals an enrichment of 4.0 wt.-%.

By changing the mass fractions given for the two nuclides, you can try to find a material composition that results in a multiplication factor of approximately 1.0. The statistical estimate for the multiplication factor along with its 95% confidence interval (1.96-sigma) is printed out by Serpent during the simulation:

------------------------------------------------------------

Serpent 2.1.29 -- Static criticality source simulation

Input file: "infinite" 

Active cycle  100 / 100  Source neutrons :  4981

Running time :                  0:00:57
Estimated running time :        0:00:57
Estimated running time left :   0:00:00

Estimated relative CPU usage :   100.0%

k-eff (analog)    = 0.83673 +/- 0.00158  [0.83363  0.83982]
k-eff (implicit)  = 0.83705 +/- 0.00067  [0.83575  0.83836]

(O4) (OMP=1) 
------------------------------------------------------------

Here, k-eff (analog) and k-eff (implicit) are two separate statistical estimators for the multiplication factor of the system that can be used to estimate the criticality of the system. As the system is currently subcritical (k-eff is smaller than 1.0), it would be a good idea to increase the ²³⁵U content slightly and re-run the calculation. Observe the changes in the k-eff.

Tune the material composition until the k-eff is approximately 1.0, i.e. at least one of the confidence intervals covers 1.0.

Calculating the flux energy spectrum

In order to calculate the flux energy spectrum in the critical system we will define a detector in the input. Detectors are described in Section 7 of the Serpent manual and can be used to calculate neutron or photon flux, reaction rate, energy spectrum, heat deposition etc. at various parts of the geometry. The short syntax for detector input can be found in the input syntax manual.

Here we will set up a simple detector (add this to the bottom of your input):

% --- Detector for tallying the flux energy spectrum
%     The energy grid used for tallying will be defined later

det EnergyDetector de MyEnergyGrid

The detector has the name EnergyDetector and the additional option de tells Serpent that we want to use an energy grid with the name MyEnergyGrid to tally the energy spectrum of the neutron flux.

We'll still need to define the energy grid (add this also):

% --- Define the energy grid to be used with the detector
%     Grid type 3 (bins have uniform lethargy width)
%     500 bins between 1e-11 MeV and 2e1 MeV.

ene MyEnergyGrid 3 500 1e-11 2e1

The energy grid has 500 bins between the energies of 1e-11 MeV and 2e1 MeV. Since the energy grid type is set to 3, Serpent will automatically divide the energy interval into the requested number of bins equally wide in lethargy.

With the detector and energy grid definitions added to the input file, you can re-run the calculation to obtain the detector output file infinite_det0.m. The structure of the detector output file is described in Section 7.2 of the Serpent manual.

You can use the OCTAVE script below to plot the flux-spectrum.

Copy and paste the contents of the OCTAVE script to a file (you can name the file, e.g. analyze.m) in the same directory as infinite_det0.m and run it with OCTAVE:

octave analyze.m

This should produce figure files FluxEInt.png and FluxEIntLinY.png to the same directory.

OCTAVE script for plotting flux spectrum. Save to analyze.m

#########################################
## Initial checking and pre-processing ##
#########################################

## Check that the detector file exists

if (exist("./infinite_det0.m", "file") != 2)
  disp("Could not find infinite_det0.m from current folder! Cannot do analysis.")
  exit()
endif

## Run the detector output file to bring the results to workspace

run infinite_det0.m;

## Check that the detector output exist

if (exist("DETEnergyDetector", "var") != 1)
  disp("Could not find results for EnergyDetector from the detector\
 file (maybe misspelled detector name?). Cannot do analysis.")
  exit()
endif

#####################################
## Plot the energy-integrated flux ##
#####################################

## Scale the energy integrated flux to a maximum of 1.0

DETEnergyDetector(:,11) = DETEnergyDetector(:,11)/max(DETEnergyDetector(:,11));

## Plot

figure('visible','off');

errorbar(DETEnergyDetectorE(:,3), DETEnergyDetector(:,11), 
         2*DETEnergyDetector(:,11).*DETEnergyDetector(:,12),'k.');

## Set axes

set(gca,'XScale','log');
set(gca,'YScale','log');
set(gca,'XTick',[1e-12,1e-10,1e-8,1e-6,1e-4,1e-2,1e0,1e2]);
set(gca,'FontSize',16);

## Make the plot a bit nicer

xlabel('Energy (MeV)')
ylabel('Energy integrated neutron flux (a.u.)')
grid on
grid minor off
box on

## Save the figure

print -dpng FluxEInt.png;

## Save the figure with linear y-axis

set(gca,'YScale','linear');
ylim([0,1]);

print -dpng FluxEIntLinY.png;

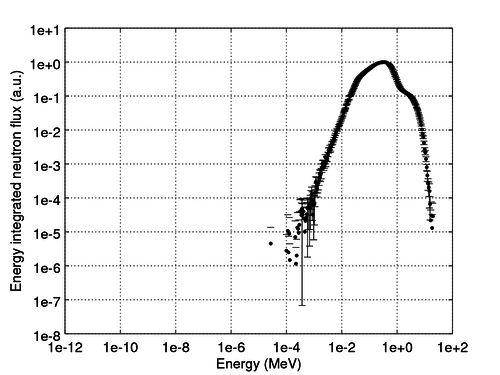
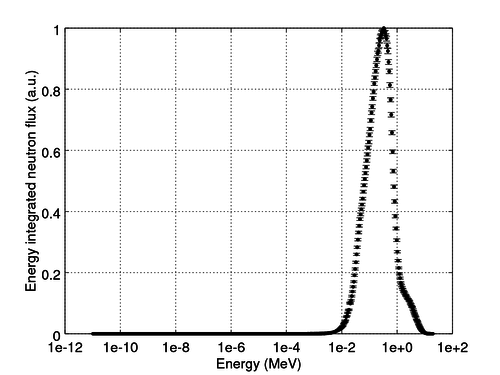
The figures should look more or less like these:

We can see that the most of the neutron flux lies between 1e-2 and 1e1 MeV, which means that the system has a very fast neutron spectrum. As there are no light elements to work as neutron moderators, this is no surprise.

Testing the effect of added moderation

We can test how the addition of some light elements, e.g. hydrogen will affect the multiplication factor and flux spectrum of the system.

Starting from the (more or less) critical material definition

% --- Fuel material (5.76 wt-% enriched uranium), density 10.1 g/cm3

mat fuel     -10.1
92235.03c    -0.0576 
92238.03c    -0.9424

we can add some hydrogen-1: The atomic number of hydrogen-1 is 1 and the mass number is also 1, which means that the basic part of the nuclide id will be 1001. We'll use the same library identifier as for the uranium, i.e. 03c:

% --- Fuel material (5.76 wt-% enriched uranium + some hydrogen), density 10.1 g/cm3
%     One part (in mass) of uranium, 0.005 parts (in mass) of hydrogen

mat fuel     -10.1
92235.03c    -0.0576 
92238.03c    -0.9424
 1001.03c    -0.005

Here we have added 0.005 parts (in mass) of hydrogen-1 to our pre-existing 1.0 parts (in mass) of uranium. You may notice that the mass fractions now sum up to more than 1.0. In such situations Serpent will automatically normalize the mass-fractions so that they add up to 1.0.

Now you can run the simulation again.

You should notice that the multiplication factor is much higher this time, indicating that the addition of moderating material to the system increased the reactivity of the system.

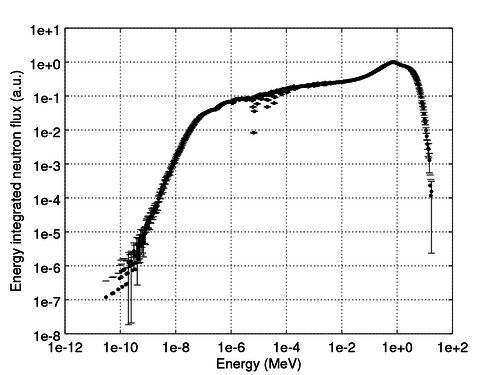
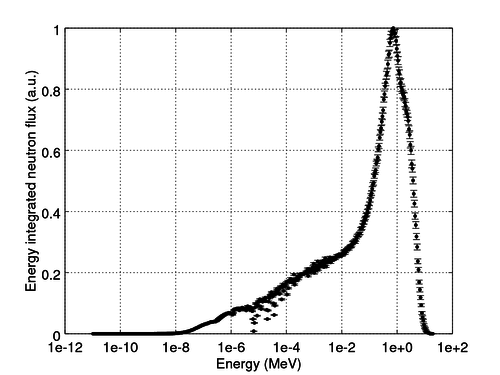
By running the OCTAVE script again, you can plot the flux-spectrum from the moderated system to obtain something like this:

Comparing these plots to the previous ones shows that the moderated system is more thermal, i.e. has higher neutron flux at the thermal energies than the unmoderated one.

Ideas for additional testing and tinkering in part 1

Remove the added hydrogen from your fuel material before moving to these additional tasks so that your system should be critical again (k-eff of approximately 1.0).

Test the effect of unresolved resonance probability table sampling on the multiplication factor and flux spectrum of the critical fast system (set ures 1). The probability table sampling should be always set on for the simulation of fast systems. Do you see an effect on the running time? You can remove the set ures 1 before moving to the next part.
Test changing the limiting surface s1 from type inf to one of the other surface types. For example, what is the multiplication factor of a cube centered at the origin (0, 0, 0) with a side-length of 10 cm cube (surface type cube, see also the input syntax for the surf command word)? Note: The unit of length in Serpent is cm. How large does the cube have to be to be considered infinite (i.e. to get the same k-eff as in the infinite system)?
Modify the input so that you have a cube with a side length of 200 cm surrounded by a 10 cm cubic layer of heavy water. You'll need to add a second cuboid surface and one more cell definition. You can use the material definition below for the heavy water. What is the multiplication factor? How thick does the heavy water layer need to be for the system to be critical?

% --- Heavy water (density 1.11 g/cm3)
%     2 parts (atomic) of hydrogen-2, 1 parts (atomic) of oxygen-16
%     Hydrogen 2 is flagged as a bound scatterer with the "moder"-card

mat heavywater -1.11 moder MyThermLib 1002
 1002.03c       2
 8016.03c       1

% --- Define thermal scattering libraries associated with hydrogen-2

therm MyThermLib hwj3.00t

Part 2: A 2D pin-cell (infinite lattice)

Part 2 overview

The second model we shall use is a 2 dimensional pin-cell model (i.e. an infinite square lattice of fuel pins). The geometry is infinite both axially and radially.

We will use this model to familiarize ourselves with the geometry and mesh-plotter capabilities in Serpent and to calculate some radial reaction rate distributions in the fuel pellet of the pin.

You can create a new folder, where you put all the files of this pin-cell model.

Part 2 input

Copy and paste the input below to a file named pin on your computer.

Colors in the input correspond to:

Comments
Control words
Name definitions
Name references

Input for 2D pin-cell geometry

% --- Simple 2D PWR pin-cell geometry for Serpent tutorial

/************************
 * Material definitions *
 ************************/

% --- Fuel material (3.0 wt-% enriched uranium dioxide), density 10.1 g/cm3

mat fuel     -10.1
92235.03c    -0.02644492
92238.03c    -0.85505247
 8016.03c    -0.11850261

% --- Cladding material for fuel rod
%     (100 % natural zirconium)

mat clad     -6.55
40000.03c    -1.0

% --- Water at 1.0 g/cm3
%     Defined using atomic fractions for the composition. 
%     Hydrogen is flagged as a bound scatterer with the "moder"-card

mat water    -1.0 moder MyThermLib 1001
 1001.03c     2.0
 8016.03c     1.0

% --- Define thermal scattering libraries associated with hydrogen in light water

therm MyThermLib lwj3.00t

/************************
 * Geometry definitions *
 ************************/

% --- Fuel pin structure

pin p1
fuel    0.4025
clad    0.4750
water

% --- Square surface with 1.5 cm side centered at (x,y) = (0,0)

surf s1 sqc 0.0 0.0 0.75

% --- Cell c1 belongs to the base universe 0, is filled with the pin p1
%     and covers everything inside surface s1

cell c1 0 fill p1   -s1

% --- Cell c2 belongs to the base universe 0, is defined as an "outside" cell
%     and covers everything outside surface s1

cell c2 0 outside    s1

/******************
 * Run parameters *
 ******************/

% --- Neutron population: 5000 neutrons per cycle, 100 active / 20 inactive cycles

set pop 5000 100 20

% --- Boundary condition (1 = black, 2 = reflective, 3 = periodic)

set bc 2

% --- Geometry plots
%     First two plots are perpendicular to z-axis i.e. xy-plots (3)

% --- First plot is 200 by 200 pixels and covers the whole geometry: -0.75 < (x,y) < 0.75

plot 3  200  200

% --- Second plot is 1000 by 1000 pixels, from axial height z = 0.0 
%     and covers more than the whole geometry: -2.25 < (x,y) < 2.25

plot 3 1000 1000 0.0 -2.25 2.25 -2.25 2.25

% --- The third plot is perpendicular to y-axis (2) i.e. an xz-plot

plot 2  200  200

% --- 200 by 200 pixel meshplot that covers the whole geometry: -0.75 < (x,y) < 0.75

mesh 3  200  200

Plotting the input

Before running a neutron transport simulation, it is typically a good idea to plot the geometry to verify that it has been defined correctly. The basics of geometry, track and mesh plotting are explained on a separate wiki page.

It is possible to execute only the geometry plotter, without running the neutron transport by using the command line argument -plot

sss2 -plot pin

Do this now. This will produce three plot files pin_geom1.png, pin_geom2.png, pin_geom3.png, which should look like the ones below:

You will probably notice that the colors in your geometry plots are a bit different from the ones shown above. If the user does not define a color for a material, Serpent will use a random color. Let's specify the colors for our materials using the rgb card. Add the bold rgb-definitions to the material definitions in your pin file:

% --- Fuel material (3.0 wt-% enriched uranium dioxide), density 10.1 g/cm3

mat fuel     -10.1 rgb 240 240 100
92235.03c    -0.02644492
92238.03c    -0.85505247
 8016.03c    -0.11850261

% --- Cladding material for fuel rod
%     (100 % natural zirconium)

mat clad     -6.55 rgb 150 150 150
40000.03c    -1.0

% --- Water at 1.0 g/cm3
%     Defined using atomic fractions for the composition. 
%     Hydrogen is flagged as a bound scatterer with the "moder"-card

mat water    -1.0 moder MyThermLib 1001 rgb 200 200 255
 1001.03c     2.0
 8016.03c     1.0

The rgb card is followed by three integer values between 0-255 for red, green and blue respectively. The ordering of additional cards in the material definition (e.g. the moder and the rgb cards) is interchangeable.

Re-plot the figures after defining the material colors. This should produce the same plots as previously, but with colors as below:

It is often a good idea to define easily distinguishable colors for each material so that they can be identified from the geometry plots. This makes it easier to spot cases, where the wrong material is used in a wrong place. Certain RGB-colors are used by Serpent to indicate specific problems with the geometry:

RGB value	Color	Description
(0, 0, 0)	COLOR	Outside cell or void-material.
(0, 255, 0)	COLOR	No cell found at coordinates.
(255, 0, 0)	COLOR	Overlap of multiple cells found at coordinates.
(255, 0, 255)	COLOR	Undefined material density factor at coordinates.

Running the input

Simply run the input from terminal, by being in the same directory as the input-file and executing

sss2 [-omp N] pin

the simulation should, again, produce multiple output files. This time a mesh-plot (pin_mesh1.png) is also produced:

The colour scheme of the mesh-plot consists of “hot” shades of red and yellow, representing relative fission power, and “cold” shades of blue, representing relative thermal flux (flux below 0.625 eV). As the mesh-plot is produced by a Monte Carlo simulation it is subject to statistical noise. The amount of statistical noise can be reduced by simulating more neutrons.

Setting up additional mesh-plots

The basic mesh-plot produced by Serpent shows the relative fission power distribution and the relative thermal flux distribution. Using detectors, it is possible to obtain a mesh-plot of many different distributions.

Let's calculate some of the reaction rate distributions by setting up detectors and linking them to additional mesh-plots:

% --- Detector that calculates the elastic scattering reaction rate in the system
%     Name of the detector is elastic.
%     The detector uses response number -3 (total elastic scattering cross section)
%     of the material at the interaction site (keyword: void)

det elastic dr -3 void

% --- A meshplot that shows the value of a detector response throughout the geometry (type 8)
%     The colormap that is used is "cold" (colormap 2)
%     The detector linked to this meshplot is named "elastic"
%     Orientation is xy (3), and output size is 200 by 200 pixel

mesh 8 2 elastic 3  200  200

% --- Detector that calculates the capture reaction rate in the system
%     Name of the detector is capture.
%     The detector uses response number -2 (total capture cross section)
%     of the material at the interaction site (keyword: void)

det capture dr -2 void

% --- A meshplot that shows the value of a detector response throughout the geometry (type 8)
%     The colormap that is used is "cold" (colormap 2)
%     The detector linked to this meshplot is named "capture"
%     Orientation is xy (3), and output size is 200 by 200 pixel

mesh 8 2 capture 3  200  200

Adding the new detector and mesh-plot definitions to the input file and re-running the simulation, will produce two additional mesh-plots:

The left figure shows the elastic scattering distribution, whereas the right figure shows the capture distribution. Darker colors indicate lower values and lighter colors indicate higher values.

Based on the two mesh-plots it is easy to see that the elastic scattering density is at its highest in water, whereas the capture density is at its highest in the fuel.

If the user does not define otherwise, the detectors will sum up responses from all materials, from all neutron energies and from all parts of the geometry. By using additional cards, the integration domain of the detector can be limited for example to include only specific materials (dm), energies (de), geometry cells (dc) or certain spatial coordinate ranges (dx, dy, dz). All of the available detector cards are detailed in the input syntax manual.

We can showcase these capabilities by modifying the capture rate detector to only include scores in the fuel-material:

% --- Detector that calculates the capture reaction rate in the fuel material
%     Name of the detector is capture.
%     The detector uses response number -2 (total capture cross section)
%     of the material at the interaction site (keyword: void)
%     Only scores interactions in material "fuel"

det capture dr -2 void dm fuel

Running the simulation again with the updated capture detector will result in a slightly different mesh-plot from the capture detector:

As the water material is no longer part of the scoring domain of the detector, the capture distribution in the fuel material is shown in greater contrast. We are now able to see that the capture rate is at its highest at the outer surface of the fuel material.

Calculating radial reaction rate distributions in the fuel pellet

The mesh-plots only show the relative values of the plotted distributions, which means that they are well suited for illustrating the shapes of the different distributions but do not provide any information on the absolute magnitude of the distributions.

In order to calculate the magnitudes (numerical values), detectors need to be set up with a suitable spatial binning. In order to calculate the radial fission and capture rate distributions in the fuel pellet, we will use a cylindrical binning for the detectors (add these to your pin-file):

% --- Detector that calculates the radial fission distribution in the fuel: 
%     Name of the detector is RadialFission.
%     The detector uses response number -6 (total fission cross section)
%     of the material at the interaction site (keyword: void)
%     Detector only scores interactions at material "fuel" ("dm fuel").
%     Detector calculates the spatial distribution using a cylindrical mesh "dn 1"
%     with 20 bins in the radial direction between 0.0 and 0.4025 cm ("0.0 0.4025 20")
%     with 1 bin in the angular direction between 0 and 360 degrees ("0 360 1")
%     with 1 bin in the axial direction that extends from -infinity to infinity ("0 0 1")

det RadialFission dr -6 void dm fuel dn 1 0.0 0.4025 20 0 360 1 0 0 1

% --- Detector that calculates the radial capture distribution in the fuel:
%     Name of the detector is RadialCapture.
%     The detector uses response number -2 (total capture cross section)
%     of the material at the interaction site (keyword: void)
%     Detector only scores interactions at material "fuel" ("dm fuel").
%     Detector calculates the spatial distribution using a cylindrical mesh "dn 1"
%     with 20 bins in the radial direction between 0.0 and 0.4025 cm ("0.0 0.4025 20")
%     with 1 bin in the angular direction between 0 and 360 degrees ("0 360 1")
%     with 1 bin in the axial direction that extends from -infinity to infinity ("0 0 1")

det RadialCapture dr -2 void dm fuel dn 1 0.0 0.4025 20 0 360 1 0 0 1

If we want to obtain absolute values for the fission rate or capture rate we will also have to specify a normalization for our calculation. We will set the power level of our pin-cell to a 200 W/cm linear power (add this to your pin-file):

% --- Set system linear power to 200 W/cm (this is a 2D system)

set power 200

As you run the simulation again, you will obtain a detector file pin_det0.m containing the output from the RadialFission and RadialCapture detectors. You can use the OCTAVE script below (you'll need to expand the element on this page to see the code) to calculate and plot radial reaction rate density distributions based on the detector-output. I.e. save the contents of the OCTAVE script to a new file called analyzePin.m in the same folder as pin_det0.m and run the script with OCTAVE.

OCTAVE script for plotting radial reaction rate distributions. Save to analyzePin.m

#########################################
## Initial checking and pre-processing ##
#########################################

## Check that the detector file exists

if (exist("./pin_det0.m", "file") != 2)
  disp("Could not find pin_det0.m from current folder! Cannot do analysis.")
  exit()
endif

## Run the detector output file to bring the results to workspace

run pin_det0.m;

## Check that the detector outputs exist

if (exist("DETRadialFission", "var") != 1)
  disp("Could not find results for RadialFission from the detector\
 file (maybe misspelled detector name?). Cannot do analysis.")
  exit()
endif

## Check that the detector outputs exist

if (exist("DETRadialCapture", "var") != 1)
  disp("Could not find results for RadialCapture from the detector\
 file (maybe misspelled detector name?). Cannot do analysis.")
  exit()
endif

################################################################################
################################################################################
## Plot the radial fission rate distribution ###################################
################################################################################
################################################################################

## Get values for radial bins

val = DETRadialFission(:,11);

## Get relative errors

relerr = DETRadialFission(:,12);

## Get minimum radius of each bin

r0 = DETRadialFissionR(:,1);

## Get maximum radius of each bin

r1 = DETRadialFissionR(:,2);

## Calculate area of each bin

A = pi*(r1.^2-r0.^2);

## Divide values by area to get average fission density from fission

val = val./A;

## Calculate absolute errors for the fission density

abserr = val.*relerr;

##########################
## open figure and plot ##
##########################

figure('visible','off');

## Draw each bin separately

hold on;

for i=1:1:size(val,1)

  ## Draw horizontal line for the mean fission density of the bin

  plot([r0(i) r1(i)], [val(i) val(i)], 'k-', 'LineWidth', 2)

  ## Draw error estimates:

  ## Mean - 2*sigma

  plot([r0(i) r1(i)], [1 1]*(val(i) - abserr(i)*2), 'r-')

  ## Mean + 2*sigma

  plot([r0(i) r1(i)], [1 1]*(val(i) + abserr(i)*2), 'r-')

  ## Draw some vertical lines to make the plot nicer

  if (i > 1)
    ## For mean:

    plot([1 1]*r0(i), [val(i-1) val(i)], 'k-', 'LineWidth', 2)

    ## For mean - 2*sigma

    plot([1 1]*r0(i), [val(i-1)-abserr(i-1)*2 val(i)-abserr(i)*2], 'r-')

    ## For mean + 2*sigma

    plot([1 1]*r0(i), [val(i-1)+abserr(i-1)*2 val(i)+abserr(i)*2], 'r-')
  end

end

## Set axes

set(gca,'FontSize',16);

## Make the plot a bit nicer

xlim([0 0.45])
xlabel('Radius (cm)')
ylabel('Fission rate density (fissions/(s*cm3))')
grid on
grid minor off
box on

## Save the figure

print -dpng RadFiss.png;

## Close all figures

close all;

################################################################################
################################################################################
## Plot the radial capture rate distribution ###################################
################################################################################
################################################################################

## Get values for radial bins

val = DETRadialCapture(:,11);

## Get relative errors

relerr = DETRadialCapture(:,12);

## Get minimum radius of each bin

r0 = DETRadialCaptureR(:,1);

## Get maximum radius of each bin

r1 = DETRadialCaptureR(:,2);

## Calculate area of each bin

A = pi*(r1.^2-r0.^2);

## Divide values by area to get average capture density from capture

val = val./A;

## Calculate absolute errors for the capture density

abserr = val.*relerr;

##########################
## open figure and plot ##
##########################

figure('visible','off');

## Draw each bin separately

hold on;

for i=1:1:size(val,1)

  ## Draw horizontal line for the mean capture density of the bin

  plot([r0(i) r1(i)], [val(i) val(i)], 'k-', 'LineWidth', 2)

  ## Draw error estimates:

  ## Mean - 2*sigma

  plot([r0(i) r1(i)], [1 1]*(val(i) - abserr(i)*2), 'r-')

  ## Mean + 2*sigma

  plot([r0(i) r1(i)], [1 1]*(val(i) + abserr(i)*2), 'r-')

  ## Draw some vertical lines to make the plot nicer

  if (i > 1)
    ## For mean:

    plot([1 1]*r0(i), [val(i-1) val(i)], 'k-', 'LineWidth', 2)

    ## For mean - 2*sigma

    plot([1 1]*r0(i), [val(i-1)-abserr(i-1)*2 val(i)-abserr(i)*2], 'r-')

    ## For mean + 2*sigma

    plot([1 1]*r0(i), [val(i-1)+abserr(i-1)*2 val(i)+abserr(i)*2], 'r-')
  end

end

## Set axes

set(gca,'FontSize',16);

## Make the plot a bit nicer

xlim([0 0.45])
xlabel('Radius (cm)')
ylabel('Capture rate density (captures/(s*cm3))')
grid on
grid minor off
box on

## Save the figure

print -dpng RadCapt.png;

Running the OCTAVE script should produce two figure files RadCapt.png and RadFiss.png that resemble the ones shown here:

As stated before, all of the results obtained from a Monte Carlo simulation are statistical estimates. This is also illustrated in the plots: the black line is based on the mean value of the tallied reaction rate, whereas the red lines correspond to the mean +- 2 standard deviations.

Looking at the plots we can see that:

Both the capture rate density and the fission rate density are at their highest at the outer surface of the pellet. This is due to flux self-shielding effects.
The difference between pellet centerline and pellet surface reaction rate densities is larger for the capture rate density.
More fissions than captures occur in the fuel.
The statistical uncertainties are larger at the pellet centerline than at the pellet surface. This is explained mostly by the fact that the width of the radial bins is equal, which leads to the area (volume) of the radial bins being larger near the surface of the pellet than in the inner parts. A larger bin will, all other things being equal, tally more interactions, which leads to better statistics (smaller statistical uncertainties).

The statistical uncertainties can be reduced by simulating more neutrons, i.e. by increasing the number of neutrons per cycle or the number of active cycles in the set pop definition:

% --- Neutron population: 5000 neutrons per cycle, 100 active / 20 inactive cycles

set pop 5000 100 20

Ideas for additional testing and tinkering in part 2

Try setting the boundary condition to vacuum (set bc 1) instead of reflective. How does the second geometry plot change? What happens to the multiplication factor? Why?
Try increasing the number of radial bins for the RadialFission and RadialCapture detectors to e.g. 200. You can compare the shapes of the distributions and the statistical uncertainties to the previously calculated ones.
Try running a simulation with more neutrons to see the effect on mesh-plots and detector results.

Part 3: A 2D assembly model (infinite lattice)

Part 3 overview

In the third part of the tutorial you will be working with a two dimensional model for one of the assembly types in an initial core loading of an EPR reactor^[1].

The assembly contains 264 fuel rods, 20 of which have burnable absorber (Gd₂O₃) intermixed in the fuel. The assembly also contains 24 control rod guide tubes and one central instrumentation thimble. The geometry of the assembly is shown below. The yellow rods contain uranium dioxide fuel with 3.0 wt-% enrichment, whereas the green rods contain uranium dioxide fuel with a 0.25 wt-% enrichment and 8.0 wt-% Gd₂O₃ as a burnable absorber.

You can create a new folder, where you put all the files of this assembly model.

Part 3 input

Copy and paste the input below to a file named assembly on your computer.

Colors in the input correspond to:

Comments
Control words
Name definitions
Name references

Input for 2D assembly geometry

% --- Simple 2D EPR assembly geometry for Serpent tutorial

/************************
 * Material definitions *
 ************************/

% --- 3.0 wt-% enriched UO2
%     Temperature is set to 950 K

mat fuelNoGad  -10.3070 tmp 950.0 rgb 255 255 150
92235.09c       -0.02644492
92238.09c       -0.85505247
 8016.09c       -0.11850261

% --- 0.25 wt-% enriched UO2 with 8.0 wt-% of Gd2O3
%     Temperature is set to 650 K

mat fuelYesGad -10.3070 tmp 650.0 rgb 150 255 150
92235.06c       -0.00202753
92238.06c       -0.80898345
 8016.06c       -0.11957908
64152.06c       -0.00013411
64154.06c       -0.00148108
64155.06c       -0.01012049
64156.06c       -0.01408805
64157.06c       -0.01083999
64158.06c       -0.01731511
64160.06c       -0.01543111

% --- Cladding material Zircaloy-4
%     [Composition from PNNL-15870, Rev. 1]

mat Zircaloy4 -6.56000E+00 tmp 610
 8016.03c  -1.19276E-03
24050.03c  -4.16117E-05
24052.03c  -8.34483E-04
24053.03c  -9.64457E-05
24054.03c  -2.44600E-05
26054.03c  -1.12572E-04
26056.03c  -1.83252E-03
26057.03c  -4.30778E-05
26058.03c  -5.83334E-06
40090.03c  -4.97862E-01
40091.03c  -1.09780E-01
40092.03c  -1.69646E-01
40094.03c  -1.75665E-01
40096.03c  -2.89038E-02
50112.03c  -1.27604E-04
50114.03c  -8.83732E-05
50115.03c  -4.59255E-05
50116.03c  -1.98105E-03
50117.03c  -1.05543E-03
50118.03c  -3.35688E-03
50119.03c  -1.20069E-03
50120.03c  -4.59220E-03
50122.03c  -6.63497E-04
50124.03c  -8.43355E-04

% --- Coolant is water with 650 ppm soluble boric acid added
%     The temperature of water is 583 K
%     Density is calculated based on a pressure of 15.5 MPa
%     Hydrogen is flagged as a bound scatterer with the "moder"-card

mat water -0.70602 tmp 583 moder lwtr 1001 rgb 200 200 255
O-16.03c   3.330861e-01
H-1.03c    6.663259e-01
B-10.03c   7.186970e-05
B-11.03c   2.892846e-04

% --- Define thermal scattering libraries associated with hydrogen in light water
%     As there are no readymade thermal scattering libraries for 583 K
%     We will tell Serpent to interpolate using two bounding libraries:
%     -lwj3.11t (H-1 in light water at 574 K)
%     -lwj3.13t (H-1 in light water at 624 K)
%     See also: https://serpent.vtt.fi/download/SSS_THERMAL.pdf

therm lwtr 583 lwj3.11t lwj3.13t

/************************
 * Geometry definitions *
 ************************/

% --- Normal fuel rod (no gadolinia in fuel)

pin FF
fuelNoGad  0.3975
void       0.4125
Zircaloy4  0.4750
water

% --- Gadolinium fuel rod

pin GG
fuelYesGad  0.3975
void        0.4125
Zircaloy4   0.4750
water

% --- Empty instrumentation thimble

pin ii
water       0.5725
Zircaloy4   0.6125
water

% --- Empty control rod channel

pin cc
water       0.5725
Zircaloy4   0.6125
water

% --- Empty lattice position (just water)

pin ww
water

% --- Pin lattice definition, name of the lattice "lat1"
%     Lattice type 1 (square lattice)
%     Lattice centered at 0.0 0.0
%     19 x 19 lattice elements (17x17 fuel rods + 1 layer of water)
%     Lattice pitch 1.26 cm
%     We'll utilize our knowledge of the 1/8 symmetry so that
%     we'll only have to type in 1/8th of the assembly

lat lat1 1 0.0 0.0 19 19 1.26
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww FF FF FF FF FF FF FF FF FF ww
ww ww ww ww ww ww ww ww ww FF FF FF FF FF FF FF FF ww ww
ww ww ww ww ww ww ww ww ww cc FF FF cc FF FF GG ww ww ww
ww ww ww ww ww ww ww ww ww FF GG FF FF FF cc ww ww ww ww
ww ww ww ww ww ww ww ww ww FF FF FF FF GG ww ww ww ww ww
ww ww ww ww ww ww ww ww ww cc FF FF cc ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww FF FF GG ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww FF FF ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ii ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww

% --- Tell Serpent to apply a symmetry to the lattice "lat1"
%     Symmetry axis is the z-axis (3)
%     Symmetry boundary condition is reflective (2)
%     Symmetry axis is located at coordinates (0.0 0.0)
%     Symmetry covers an angle starting from 270 degrees
%     and extending for 45 degrees

set usym lat1 3 2 0.0 0.0 270 45

% --- A square surface around the fuel assembly

surf s1 sqc  0.0 0.0 10.752

% --- Cell c1 belongs to the base universe 0, is filled with the lattice lat1
%     and covers everything inside surface s1

cell c1 0 fill lat1     -s1

% --- Cell c2 belongs to the base universe 0, is defined as an "outside" cell
%     and covers everything outside surface s1

cell c2 0 outside        s1

/******************
 * Run parameters *
 ******************/

% --- Assembly linear power is 420 kW

set power 42000

% --- Boundary condition (1 = black, 2 = reflective, 3 = periodic)

set bc 2

% --- Neutron population: 10000 neutrons per cycle, 100 active / 20 inactive cycles

set pop 10000 100 20

% --- XY-plot (3), which is 700 by 700 pixels and covers the whole geometry

plot 3 700 700

% --- XY-meshplot (3), which is 700 by 700 pixels and covers the whole geometry

mesh 3 700 700

Running the input for the assembly geometry

Simply run the input from terminal, by being in the same directory as the input-file and executing

sss2 [-omp N] assembly

the simulation should, again, produce multiple output files and also the geometry and mesh-plots:

Based on the mesh-plot, we can see that the fission power is much lower in the fuel rods that contain the burnable absorber (BA) than in the normal fuel rods. The BA-rods also create a depression (decrease) in the thermal flux distribution in their immediate surroundings.

Increasing the number of simulated neutrons will increase the simulation time, but reduce the statistical noise in the mesh-plot. For example, simulating 15000 active cycles with 20000 neutrons in each cycle will result in this:

Testing the power feedback effects in the assembly

One important part of safe reactor design is to ensure that the power reactivity feedbacks for the reactor are negative in the operating conditions. This means that changes that follow from increased reactor power (such as increase in fuel and coolant/moderator temperature) decrease the multiplication factor of the system.

We will test the negativity of these feedbacks in our fuel assembly model.

Make a note of the multiplication factor you obtained from the first simulation, for example:

k-eff (implicit)  = 0.98086 +/- 0.00069  [0.97950  0.98222]

Let's assume that an increase in reactor power will bring about the following changes in material temperatures and densities:

Fuel temperature for non-burnable absorber rods will increase by 300 K.
Fuel temperature for burnable absorber rods will increase by 50 K.
Moderator temperature will increase by 25 K.
Moderator density will decrease to 0.635 g/cm³.

We'll calculate the effects these changes have on the multiplication factor of our assembly. The next subsections will give information on how to apply these changes to the input.

Changing the fuel temperature

For the fuel materials we can simply change the value in the tmp card in the material definition.

For the non-gadolinia fuel we will change the definition to

mat fuelNoGad  -10.3070 tmp 1250.0 rgb 255 255 150
92235.09c       -0.02644492
92238.09c       -0.85505247
 8016.09c       -0.11850261

And for the gadolinia containing fuel we will use

mat fuelYesGad -10.3070 tmp 700.0 rgb 150 255 150
92235.06c       -0.00202753
92238.06c       -0.80898345
 8016.06c       -0.11957908
64152.06c       -0.00013411
64154.06c       -0.00148108
64155.06c       -0.01012049
64156.06c       -0.01408805
64157.06c       -0.01083999
64158.06c       -0.01731511
64160.06c       -0.01543111

Changing the water temperature

For the water temperature change, we'll need to modify both the value in the tmp card of the material definition and the value in the therm definition:

mat water -0.70602 tmp 608 moder lwtr 1001 rgb 200 200 255
O-16.03c   3.330861e-01
H-1.03c    6.663259e-01
B-10.03c   7.186970e-05
B-11.03c   2.892846e-04

and

therm lwtr 608 lwj3.11t lwj3.13t

Changing the water density

For the water density change, it is enough to change the mass density given in the material definition:

mat water -0.635 tmp 608 moder lwtr 1001 rgb 200 200 255
O-16.03c   3.330861e-01
H-1.03c    6.663259e-01
B-10.03c   7.186970e-05
B-11.03c   2.892846e-04

Calculating the k-eff for the modified system

After applying all of the changes to your input, you can run the simulation again to see the effect on the multiplication factor. Make a note of the new multiplication factor, e.g.

k-eff (implicit)  = 0.96574 +/- 0.00073  [0.96430  0.96718]

Comparing the new multiplication factor to the previously obtained we see that our modifications resulted in a clear decrease in the multiplication factor: It went from 0.98086 +/- 0.00069 to 0.96574 +/- 0.00073. The feedback effect seems to be negative in our assembly, as it should be.

Calculating the pin power distribution

In safety analysis, the pin power distribution in each assembly is often a requested output from neutronics calculations. The pin power distribution helps in identifying the limiting fuel rod, i.e. the fuel rod with the highest fuel centerline temperature or highest heat flux at the cladding surface.

We'll use a simple mesh-detector to calculate the pin power distribution for our assembly:

% --- Detector that calculates the pin power distribution in the assembly: 
%     Name of the detector is pinpowers.
%     The detector uses response number -8 (fission heat deposition)
%     of the material at the interaction site (keyword: void).
%     The detector has 17 bins in the x-direction between -10.71 cm and 10.71 cm
%     The detector has 17 bins in the y-direction between -10.71 cm and 10.71 cm

det pinpowers dr -8 void dx -10.71 10.71 17 dy -10.71 10.71 17

Add the detector definition to your input and run the calculation again. The calculation will now produce the detector output file assembly_det0.m that contains the results for our newly defined detector. You can use the OCTAVE script below (you'll need to expand the element on this page to see the code) to calculate and plot radial reaction rate density distributions based on the detector-output. I.e. save the contents of the OCTAVE script to a new file called analyzeAssembly.m in the same folder as assembly_det0.m and run the script with OCTAVE.

OCTAVE script for plotting pin power distribution. Save to analyzeAssembly.m

#########################################
## Initial checking and pre-processing ##
#########################################

## Check that the detector file exists

if (exist("./assembly_det0.m", "file") != 2)
  disp("Could not find assembly_det0.m from current folder! Cannot do analysis.")
  exit()
endif

## Run the detector output file to bring the results to workspace

run assembly_det0.m;

## Check that the detector outputs exist

if (exist("DETpinpowers", "var") != 1)
  disp("Could not find results for pinpowers from the detector\
 file (maybe misspelled detector name?). Cannot do analysis.")
  exit()
endif

#####################################
## Plot the pin power distribution ##
#####################################

## Get values for pin powers

val = DETpinpowers(:,11);

## Remove zero-values (control rod channels)

val(val==0) = NaN;

## Get relative errors

relerr = DETpinpowers(:,12);

## Reshape the arrays

val    = reshape(val, [17, 17]);
relerr = reshape(relerr, [17, 17]);

## Calculate absolute errors

abserr = val.*relerr*2;

##########################
## open figure and plot ##
##########################

figure('visible','off');

## 2D color plot of the values

imagesc(val);

## Change the color scheme to something better

colormap("autumn");

## Add a colorbar

cb = colorbar();

## Tune the colorbar and label text

set(cb, 'FontSize',16);
set(cb, 'Ylabel', 'Linear power (W/cm)');
h = get(cb, 'YLabel');
set(h, 'FontSize',16);

## Add numbers for each rod

for i=1:1:17
  for j=1:1:17

    ## Calculate x and y position for the text of current rod

    x    = i-0.35 ;
    y    = j-0.2;
    xerr = i-0.46;
    yerr = j+0.2;

    ## Get current rod linear power (rounded to W/cm)

    curval = round(val(i,j));
    curerr = round(abserr(i,j)*10)/10;

    ## Add text for current rod

    if (! isnan(curval))

      ## Linear power

      text(x, y, num2str(curval), 'FontSize', 7);

      ## +- 2*sigma uncertainty

      text(xerr, yerr, ["+- " num2str(curerr)], 'FontSize', 7);

    endif
  endfor

  ## Add some lines to make the picture nicer

  line([0.5 17.5], [i i]+0.5);
  line([i i]+0.5, [0.5 17.5]);

endfor

## Make the plot a bit nicer by removing the tick-marks

set(gca, 'XTick', []);
set(gca, 'YTick', []);

## Add title to the plot

title("Pin power distribution (linear powers +- 2*sigma uncertainty)")

## Save the figure

print -dpng PinPowers.png;

## Close all figures

close all;

Running the OCTAVE script should produce a figure file PinPowers.png that resembles the one shown here:

The figure shows the linear power of each pin by color and as text. The maximum linear powers are around 180 W/cm and are located in the lattice positions both at the assembly outer boundary and around the central instrumentation thimble. The linear power of the burnable absorber rods is significantly lower, approximately 14W/cm.

Even though the assembly is symmetric, the power distribution is not exactly symmetric. This is again due to the statistical nature of Monte Carlo transport. Typically one can average the results from symmetrical lattice positions as a part of the post processing to obtain a symmetric distribution.

Ideas for additional testing and tinkering in part 3

Part 4: Assembly burnup calculation

Part 4 overview

In this part of the tutorial you will conduct a burnup (depletion) calculation for the 2D assembly model presented previously.

You can create a new folder, where you put all the files of this assembly burnup calculation.

Part 4 input

The input is the same as in the previous part of the tutorial except for a few differences:

The two fuel materials are flagged as burnable materials with the burn 1 card in the material definition.
The temperature of fuelYesGad is also set to 950 K.
The neutron population is reduced to 5000 neutrons per cycle, 100 active / 20 inactive cycles to reduce the calculation time.
There are several new definitions under the title Settings for the burnup calculation in the end of the input file.

Copy and paste the input below to a file named burn on your computer.

Colors in the input correspond to:

Comments
Control words
Name definitions
Name references

Input for assembly burnup calculation

% --- Simple 2D EPR assembly geometry burnup model for Serpent tutorial

/************************
 * Material definitions *
 ************************/

% --- 3.0 wt-% enriched UO2
%     Temperature is set to 950 K

mat fuelNoGad  -10.3070 tmp 950.0 rgb 255 255 150 burn 1
92235.09c       -0.02644492
92238.09c       -0.85505247
 8016.09c       -0.11850261

% --- 0.25 wt-% enriched UO2 with 8.0 wt-% of Gd2O3
%     Temperature is set to 950 K

mat fuelYesGad -10.3070 tmp 950.0 rgb 150 255 150 burn 1
92235.09c       -0.00202753
92238.09c       -0.80898345
 8016.09c       -0.11957908
64152.09c       -0.00013411
64154.09c       -0.00148108
64155.09c       -0.01012049
64156.09c       -0.01408805
64157.09c       -0.01083999
64158.09c       -0.01731511
64160.09c       -0.01543111

% --- Cladding material Zircaloy-4
%     [Composition from PNNL-15870, Rev. 1]

mat Zircaloy4 -6.56000E+00 tmp 610
 8016.03c  -1.19276E-03
24050.03c  -4.16117E-05
24052.03c  -8.34483E-04
24053.03c  -9.64457E-05
24054.03c  -2.44600E-05
26054.03c  -1.12572E-04
26056.03c  -1.83252E-03
26057.03c  -4.30778E-05
26058.03c  -5.83334E-06
40090.03c  -4.97862E-01
40091.03c  -1.09780E-01
40092.03c  -1.69646E-01
40094.03c  -1.75665E-01
40096.03c  -2.89038E-02
50112.03c  -1.27604E-04
50114.03c  -8.83732E-05
50115.03c  -4.59255E-05
50116.03c  -1.98105E-03
50117.03c  -1.05543E-03
50118.03c  -3.35688E-03
50119.03c  -1.20069E-03
50120.03c  -4.59220E-03
50122.03c  -6.63497E-04
50124.03c  -8.43355E-04

% --- Coolant is water with 650 ppm soluble boric acid added
%     The temperature of water is 583 K
%     Density is calculated based on a pressure of 15.5 MPa
%     Hydrogen is flagged as a bound scatterer with the "moder"-card

mat water -0.70602 tmp 583 moder lwtr 1001 rgb 200 200 255
O-16.03c   3.330861e-01
H-1.03c    6.663259e-01
B-10.03c   7.186970e-05
B-11.03c   2.892846e-04

% --- Define thermal scattering libraries associated with hydrogen in light water
%     As there are no readymade thermal scattering libraries for 583 K
%     We will tell Serpent to interpolate using two bounding libraries:
%     -lwj3.11t (H-1 in light water at 574 K)
%     -lwj3.13t (H-1 in light water at 624 K)
%     See also: https://serpent.vtt.fi/download/SSS_THERMAL.pdf

therm lwtr 583 lwj3.11t lwj3.13t

/************************
 * Geometry definitions *
 ************************/

% --- Normal fuel rod (no gadolinia in fuel)

pin FF
fuelNoGad  0.3975
void       0.4125
Zircaloy4  0.4750
water

% --- Gadolinium fuel rod

pin GG
fuelYesGad  0.3975
void        0.4125
Zircaloy4   0.4750
water

% --- Empty instrumentation thimble

pin ii
water       0.5725
Zircaloy4   0.6125
water

% --- Empty control rod channel

pin cc
water       0.5725
Zircaloy4   0.6125
water

% --- Empty lattice position (just water)

pin ww
water

% --- Pin lattice definition, name of the lattice "lat1"
%     Lattice type 1 (square lattice)
%     Lattice centered at 0.0 0.0
%     19 x 19 lattice elements (17x17 fuel rods + 1 layer of water)
%     Lattice pitch 1.26 cm
%     We'll utilize our knowledge of the 1/8 symmetry so that
%     we'll only have to type in 1/8th of the assembly

lat lat1 1 0.0 0.0 19 19 1.26
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww FF FF FF FF FF FF FF FF FF ww
ww ww ww ww ww ww ww ww ww FF FF FF FF FF FF FF FF ww ww
ww ww ww ww ww ww ww ww ww cc FF FF cc FF FF GG ww ww ww
ww ww ww ww ww ww ww ww ww FF GG FF FF FF cc ww ww ww ww
ww ww ww ww ww ww ww ww ww FF FF FF FF GG ww ww ww ww ww
ww ww ww ww ww ww ww ww ww cc FF FF cc ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww FF FF GG ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww FF FF ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ii ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww

% --- Tell Serpent to apply a symmetry to the lattice "lat1"
%     Symmetry axis is the z-axis (3)
%     Symmetry boundary condition is reflective (2)
%     Symmetry axis is located at coordinates (0.0 0.0)
%     Symmetry covers an angle starting from 270 degrees
%     and extending for 45 degrees

set usym lat1 3 2 0.0 0.0 270 45

% --- A square surface around the fuel assembly

surf s1 sqc  0.0 0.0 10.752

% --- Cell c1 belongs to the base universe 0, is filled with the lattice lat1
%     and covers everything inside surface s1

cell c1 0 fill lat1     -s1

% --- Cell c2 belongs to the base universe 0, is defined as an "outside" cell
%     and covers everything outside surface s1

cell c2 0 outside        s1

/******************
 * Run parameters *
 ******************/

% --- Assembly linear power is 420 kW

set power 42000

% --- Boundary condition (1 = black, 2 = reflective, 3 = periodic)

set bc 2

% --- Neutron population: 5000 neutrons per cycle, 100 active / 20 inactive cycles

set pop 5000 100 20

% --- XY-plot (3), which is 700 by 700 pixels and covers the whole geometry

plot 3 700 700

% --- XY-meshplot (3), which is 700 by 700 pixels and covers the whole geometry

mesh 3 700 700

/***************************************
 * Settings for the burnup calculation *
 ***************************************/

% --- Burnup points for the burnup calculation (in MWd/kgU)
%     Too long intervals between the burnup points will decrease the
%     accuracy of the burnup calculation, especially during the burn-out 
%     of burnable absorber 

dep butot 0.1  0.5  1  3  5  7  9  11  13  15  17  19

% --- Material division for burnup calculation
%     Treat different pins of fuelNoGad as separate depletion zones (sep 1)

div fuelNoGad  sep 1

% --- Material division for burnup calculation
%     Treat different pins of fuelYesGad as separate depletion zones (sep 1)
%     additionally divide each of those fuel pellets into 10 equal volume rings
%     between radial coordinates of 0.0 and 0.3975

div fuelYesGad sep 1 subr 10 0.0 0.3975

% --- Calculate material volumes before simulation by
%     sampling 10 million random points in the geometry.
%     Specifying the material volumes is crucial in burnup calculations

set mcvol 10000000

% --- Nuclide inventory: these nuclides will be included in the
%     depletion output file burn_dep.m. The list can be changed
%     after the simulation has concluded if needed. Then you can run
%     sss2 -rdep burn
%     which will make Serpent re-read the inventory and re-produce the
%     depletion output file.

set inventory
 922350
 942390
 641550
 641570

% --- Use predictor corrector method for the depletion solution
%     leli: Linear extrapolation on predictor
%           Linear interpolation on corrector
%     10 10: 10 substeps on predictor, 10 substeps on corrector

set pcc leli 10 10

% --- Decay data library needs to be specified for burnup calculations

set declib "sss_jeff31.dec"

% --- Neutron induced fission yield library needs to be specified for
%     burnup calculations

set nfylib "sss_jeff31.nfy"

% --- Reduce unionized energy grid size in order to save some memory
%     Use grid thinning with 5e-5 reconstruction tolerance between
%     1e-9 and 15 MeV.

set egrid 5e-5 1e-9 15.0

Depletion zone division

In burnup calculations it is usually necessary to subdivide the materials into multiple depletion zones. This is due to the fact that even if the material composition is initially the same in multiple different fuel rods, the differences in the local neutron flux between, e.g. different lattice positions should produce different compositions for the depleted fuel. Similarly, fuel rods that contain burnable absorber should be divided into rings to accurately capture the radial burn-out of the absorber. Significant errors may be introduced to the results if materials are not correctly divided to depletion zones.

Serpent has an easy to use methodology for automatically dividing the materials into user specified depletion zones. This might be a good time to visit the wiki-page describing that capability: Automated depletion zone division

In the input above, all of the unique lattice positions are treated as a separate depletion zone and the burnable absorber rods are further subdivided into 10 rings of equal area using the div definitions:

% --- Material division for burnup calculation
%     Treat different pins of fuelNoGad as separate depletion zones (sep 1)

div fuelNoGad  sep 1

% --- Material division for burnup calculation
%     Treat different pins of fuelYesGad as separate depletion zones (sep 1)
%     additionally divide each of those fuel pellets into 10 equal volume rings
%     between radial coordinates of 0.0 and 0.3975

div fuelYesGad sep 1 subr 10 0.0 0.3975

Specifying material volumes

It is important to make certain that Serpent uses the correct material volumes in burnup calculations. Serpent will automatically try to estimate the material volumes for each input but this will only yield good results in simple 2D cases. This will fail for certain in any geometries containing symmetries in the fuel assemblies.

See: Defining material volumes

Usually it is best to check the material volumes using the

sss2 -checkvolumes POINTS input

command. In this example, we have told Serpent to sample 10 million random points in the geometry before the calculation to obtain a statistical estimate of the material volumes and use those volumes for the burnup calculation:

% --- Calculate material volumes before simulation by
%     sampling 10 million random points in the geometry.
%     Specifying the material volumes is crucial in burnup calculations

set mcvol 10000000

Using more points will yield more accurate estimates for the volumes but will take more time.

Running the burnup calculation

Run the burnup simulation, preferably using OpenMP parallelization (try e.g. N = 4) as the burnup calculations tend to take a long time:

sss2 -omp N burn

During the simulation, Serpent executes two neutron transport solutions for each burnup step, meaning that the whole simulation will take a while (30 minutes to several hours depending on computer and parallelization).

The simulation will produce a separate mesh-plot for each burnup point:

The mesh-plots show that the burnable absorber rods begin to produce some fission power as the burnable absorber is consumed from them. The maximum of the fission power distribution also seems to move to the inner parts of the assembly from the outer part during the fuel depletion.

The depletion results, e.g. the specified nuclide inventories, material specific burnups and nuclide inventories are printed into the output file burn_dep.m. The results from the neutron transport simulation at each burn up point (e.g. estimates for multiplication factor) are appended to the main results file burn_res.m.

Changes in assembly due to burnup

We can use the results produced by the simulation to analyze the evolution of the multiplication factor as well as the masses of some interesting nuclides during the burnup calculation.

You can use the OCTAVE script below (you'll need to expand the element on this page to see the code) to calculate and plot some burnup depended quantities based on the results of the burnup calculation. I.e. save the contents of the OCTAVE script to a new file called analyzeBurn.m in the same folder as burn_res.m and burn_dep.m and run the script with OCTAVE.

OCTAVE script for plotting burnup dependent results. Save to analyzeBurn.m

#########################################
## Initial checking and pre-processing ##
#########################################

## Check that the main results file exists

if (exist("./burn_res.m", "file") != 2)
  disp("Could not find burn_res.m from current folder! Cannot do analysis.")
  exit()
endif

## Check that the depletion output file exists

if (exist("./burn_dep.m", "file") != 2)
  disp("Could not find burn_dep.m from current folder! Cannot do analysis.")
  exit()
endif

## Run both of the files to bring the results to workspace

run burn_res.m;
run burn_dep.m;

###############################################
## Plot the multiplication factor vs. burnup ##
###############################################

figure('visible','off');
errorbar(BU, IMP_KEFF(:,1), IMP_KEFF(:,1).*IMP_KEFF(:,2)*2,'k.')

## Set font size for the axes

set(gca, 'FontSize',16);

## Add labels for the axes

xlabel("Burnup (MWd/kgU)");
ylabel("Multiplication factor");

## Add title to the plot

title("Multiplication factor of the assembly as a function of burnup")

## Set limits for the axes

xlim([0 20]);
ylim([0.95 1.05]);

## Make the plot a bit nicer

grid on;
box on;

## Save the figure

print -dpng Keff.png;

## Close all figures

close all;

###############################
## Plot U235 mass vs. burnup ##
###############################

figure('visible','off');
plot(BU, TOT_MASS(iU235, :), 'k.-')

## Set font size for the axes

set(gca, 'FontSize',16);

## Add labels for the axes

xlabel("Burnup (MWd/kgU)");
ylabel("U-235 mass (g/cm of axial height)");

## Add title to the plot

title("U-235 mass in the assembly as a function of burnup")

## Set limits for the axes

xlim([0 20]);
ylim([0 35]);

## Make the plot a bit nicer

grid on;
box on;

## Save the figure

print -dpng mU235.png;

################################
## Plot Pu239 mass vs. burnup ##
################################

figure('visible','off');
plot(BU, TOT_MASS(iPu239, :), 'k.-')

## Set font size for the axes

set(gca, 'FontSize', 16);

## Add labels for the axes

xlabel("Burnup (MWd/kgU)");
ylabel("Pu-239 mass (g/cm of axial height)");

## Add title to the plot

title("Pu-239 mass in the assembly as a function of burnup")

## Make the plot a bit nicer

grid on;
box on;

## Save the figure

print -dpng mPu239.png;

## Close all figures

############################################
## Plot Gd155 and Gd157 masses vs. burnup ##
############################################

figure('visible','off');
plot(BU, TOT_MASS(iGd155, :), 'b.-')
hold on
plot(BU, TOT_MASS(iGd157, :), 'r.-')
hold off

## Add a legend

h1 = legend("Gd-155", "Gd-157", "location", "northeast");

## Set font size for the legend

set(h1, "FontSize", 16);

## Set font size for the axes

set(gca, "FontSize", 16);

## Add labels for the axes

xlabel("Burnup (MWd/kgU)");
ylabel("Mass (g/cm of axial height)");

## Add title to the plot

title("Gd-155 and Gd-157 mass in the assembly as a function of burnup")

## Set limits for the axes

xlim([0 20]);
ylim([0 1.2]);

## Make the plot a bit nicer

grid on;
box on;

## Save the figure

print -dpng mGd.png;

## Close all figures

close all;

Running the script will produce four figure files:

Keff.png: The multiplication factor of the assembly as a function of burnup.
mGd.png: The masses of ¹⁵⁵Gd and ¹⁵⁷Gd isotopes in the assembly (per unit length) as a function of burnup.
mU235.png: The mass of ²³⁵U in the assembly (per unit length) as a function of burnup.
mPu239.png: The mass of ²³⁹Pu in the assembly (per unit length) as a function of burnup.

The Keff.png plot should resemble this one:

We can see that the initial multiplication factor is approximately 0.98 and it decreases sharply during the first step of the calculation. This is due to the production of neutron absorbing fission products (neutron poisons). The concentrations of these neutron absorbers soon reach an equilibrium and the multiplication factor does not decrease any more. On the contrary, the multiplication factor starts to increase due to the fact that the neutron absorbers in the burnable absorber rods (mainly ¹⁵⁵Gd and ¹⁵⁷Gd) are consumed (see the next picture: mGd.png). Between 11 and 13 Mwd/kgU the last of the burnable absorbers are removed and the multiplication factor does not increase any more. Instead, it begins to fall due to the consumption of the initial fissile isotope ²³⁵U (see mU235.png) although the fissile nuclide ²³⁹Pu is also produced from ²³⁸U (see mPu239.png).

The other figures should look like these:

mGd.png:

mU235.png:

mPu239.png:

It should be noted that the nuclide densities printed in burn_dep.m are statistical estimates and thus contain a statistical uncertainty. However, the statistical uncertainty of the nuclide densities cannot be easily calculated inside the Serpent simulation and typically the best way to estimate this uncertainty is to execute the same burnup simulation many times (e.g. tens of times) using different random number seeds and looking at the differences in the resulting nuclide densities.

Ideas for additional testing and tinkering in part 4

Part 5: A 3D research reactor model

Part 5 overview

In this last part of the tutorial you will build a Serpent model for an imaginary low power pool-type research reactor core. The reactor is inspired partly by critical pin-lattice configurations and partly by the TRIGA research reactor type.

The (simplified) geometry of the reactor is shown below for an xy-cut at axial midplane of the core and xz-cuts at core center and at the control rods:

Below is the overview of the core:

The core contains 493 fuel rods (length 50 cm) with 3.0 wt-% enriched fuel. The fuel rods are similar to the non burnable absorber rods used in the EPR example.
The core contains four movable boron carbide control rods located symmetrically around the core.
The core is reflected by a circular graphite reflector.
The core is located in a light water pool.
The core has two 2 cm thick steel grid plates with holes for the fuel rods and control rods. There are some empty positions where additional fuel rods could be added at the periphery of the core. The two grids are identical, with the top grid shown here:

The empty lattice positions can be seen as blue circles, whereas the lattice positions filled with fuel rods are seen in light grey. The positions of the four control rods are seen as dark grey circles, surrounded with light blue water.

Part 5 geometry details

Radial geometry

This section details the measures needed to build the geometry model for the core. The general radial geometry can be summarized as:

The outer radius of the grid plates is 26 cm.
The inner radius of the graphite reflector is 30 cm.
The outer radius of the graphite reflector is 60 cm.
The outer radius of the model is 100 cm.

Axial geometry

The height of the graphite reflector is 100 cm and it covers the active fuel height symmetrically.

The bottom of the model is 100 cm below axial midplane.
The bottom of the graphite reflector is 50 cm below axial midplane.
The bottom of the lower grid plate is 37 cm below axial midplane, which is also the bottom of fuel rods and the bottom of the control rod guide tubes.
The top of the lower grid plate is 35 cm below axial midplane.
The bottom of active fuel is 25 cm below the axial midplane.
The top of active fuel is 25 cm above the axial midplane.
The bottom of of the upper grid plate is 30 cm above axial midplane
The top of of the upper grid plate is 32 cm above axial midplane
The top of of the fuel rods is 35 cm above axial midplane.
The top of the graphite reflector is 50 cm above axial midplane.
The top of the model is 100 cm above axial midplane.

Lattice and grid plate geometry

The core lattice is a square lattice with a lattice pitch of 1.8 cm. The grid plates contain 4 holes for control rods and 583 holes for fuel rods in a roughly circular shape. 493 of the fuel rod positions are filled with fuel rods. The core lattice exhibits a 1/8 (45 degree) symmetry.

The outer radius of the grid plates is 26 cm.
The radius of the control rod holes in the grid plates is 0.85 cm.
The radius of the fuel rod holes in the grid plates is 0.485 cm.

Fuel rod geometry

The fuel rod geometry is shown below (contracted axially by a factor of 7).

The radial geometry of the active fuel part is as follows:

Fuel pellet outer radius 0.3975 cm.
Cladding inner radius 0.4125 cm.
Cladding outer radius 0.4750 cm.

The region between the fuel pellet and cladding is filled with a fill gas, but can be modelled as void.

The end-plugs below and above the active fuel consist of solid cladding material and have an outer radius equal to the cladding outer radius (0.4750 cm).

Control rod geometry

The control rods move in their guide tubes and they consist axially of three parts:

Bottom 12 cm is made of stainless steel.
The absorber part is 50 cm long and made out of boron carbide (B₄C).
The top part is made of stainless steel and extends out of the reactor to the control rod drive system (not included in the model).

The outer radius of the control rods is a constant 0.60 cm for all of the axial parts.

The guide tubes extend from the bottom of the bottom plate to the top of the model and are normally filled with water. The guide tubes are made of Zircaloy-4 and their radial dimensions are given below:

Guide tube inner radius 0.75 cm.
Guide tube outer radius 0.80 cm.

The figures below show the control rods in their fully inserted and fully withdrawn positions. In the fully inserted position the absorber part of the control rods coincides with the active fuel part of the fuel rods. The travel distance between the fully inserted and fully withdrawn positions is 50 cm (the same as the absorber length).

Part 5 material details

The reactor contains six different materials:

Uranium dioxide fuel with 3.0 wt-% enrichment and a density of 10.37 g/cm³.
Zircaloy-4 as the cladding and guide tube material. Density 6.56 g/cm³.
Normal light water (density 1.0 g/cm³) filling the reactor pool and guide tubes.
Graphite (density 1.719 g/cm³) as a radial reflector.
Boron carbide (B₄C) as the control rod absorber material. Density 2.52 g/cm³.
Stainless steel as the grid plates and in the non-absorbing part of the control rods. Density 8.0 g/cm³.

The material definitions are given below

Colors in the input correspond to:

Comments
Control words
Name definitions
Name references

Material definitions for research reactor. Copy to a file named materials.

/************************
 * Material definitions *
 ************************/

% --- 3.0 wt-% enriched uranium dioxide fuel
%     Density of the fuel 10.307 g/cm3.

mat fuel    -10.3070 rgb 255 255 150
92235.03c    -0.02644492
92238.03c    -0.85505247
 8016.03c    -0.11850261

% --- Cladding material Zircaloy-4
%     [Composition from PNNL-15870, Rev. 1]
%     Density 6.56 g/cm3

mat Zircaloy4 -6.56000E+00 rgb 200 200 200
 8016.03c     -1.19276E-03
24050.03c     -4.16117E-05
24052.03c     -8.34483E-04
24053.03c     -9.64457E-05
24054.03c     -2.44600E-05
26054.03c     -1.12572E-04
26056.03c     -1.83252E-03
26057.03c     -4.30778E-05
26058.03c     -5.83334E-06
40090.03c     -4.97862E-01
40091.03c     -1.09780E-01
40092.03c     -1.69646E-01
40094.03c     -1.75665E-01
40096.03c     -2.89038E-02
50112.03c     -1.27604E-04
50114.03c     -8.83732E-05
50115.03c     -4.59255E-05
50116.03c     -1.98105E-03
50117.03c     -1.05543E-03
50118.03c     -3.35688E-03
50119.03c     -1.20069E-03
50120.03c     -4.59220E-03
50122.03c     -6.63497E-04
50124.03c     -8.43355E-04

% --- Graphite consisting of natural carbon
%     Flagged as bound scatterer with the "moder"-card

mat graphite -1.719 moder graphiteLib 6000 rgb 50 50 50
 6000.03c          1.00

% --- Thermal scattering libraries for graphite at room temperature

therm graphiteLib grj3.00t

% --- Boron carbide (B4C)

mat B4C -2.52000E+00 rgb 100 200 100
 5010.03c  -1.44242E-01
 5011.03c  -6.38368E-01
 6012.03c  -2.14872E-01

% --- Stainless steel type 304
%     [Composition from PNNL-15870, Rev. 1]

mat ssteel -8.00000E+00 rgb 140 140 140
 6012.03c  -3.95366E-04
14028.03c  -4.59332E-03
14029.03c  -2.41681E-04
14030.03c  -1.64994E-04
15031.03c  -2.30000E-04
16032.03c  -1.42073E-04
16033.03c  -1.15681E-06
16034.03c  -6.75336E-06
16036.03c  -1.68255E-08
24050.03c  -7.93000E-03
24052.03c  -1.59029E-01
24053.03c  -1.83798E-02
24054.03c  -4.66139E-03
25055.03c  -1.00000E-02
26054.03c  -3.96166E-02
26056.03c  -6.44901E-01
26057.03c  -1.51600E-02
26058.03c  -2.05287E-03
28058.03c  -6.21579E-02
28060.03c  -2.47678E-02
28061.03c  -1.09461E-03
28062.03c  -3.54721E-03
28064.03c  -9.32539E-04

% --- Coolant is water
%     The temperature of water is 300 K
%     Hydrogen is flagged as a bound scatterer with the "moder"-card

mat water -1.0000 moder lwtr 1001 rgb 200 200 255
 8016.03c   1.0
 1001.03c   2.0

% --- Thermal scattering libraries for hydrogen in light water
%     at room temperature

therm lwtr lwj3.00t

Building the Serpent model for the reactor

Initial input

We will start to build our Serpent model for the research reactor by copying the material definitions from above to a file called materials. We can include this file to our main input file and keep our main input file short and simple.

We'll start building the main input from the version shown below. Copy and paste the input below to a file named reactor on your computer.

Colors in the input correspond to:

Comments
Control words
Name definitions
Name references

Input for 3D research reactor geometry. Save to reactor

% --- Research reactor input for Serpent tutorial

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% We'll start from a simple water geometry %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% --- Our reactor model will fit inside a cubic surface with an edge length of 100 cm

surf sCUBE cube 0.0 0.0 0.0 100.0

% --- Cell cIN contains water

cell cIN  0 water   -sCUBE

% --- Cell cOUT is defined as an outside cell

cell cOUT 0 outside  sCUBE

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Link additional input files here %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% --- Link the materials file to this input
 
include "materials"

/******************
 * Run parameters *
 ******************/

% --- Neutron population: 10000 neutrons per cycle, 100 active / 50 inactive cycles

set pop 10000 100 50

% --- Geometry plots

% --- XY-plot

plot 3 200 200 0 -100 100 -100 100

% --- XZ-plot

plot 2 200 200 0 -100 100 -100 100

If you now plot the geometry with

sss2 -plot reactor

you will notice that the geometry is currently simply a cubic water system:

Coarse radial model

As we don't want to model an empty water system, but a research reactor we'll need to work on the geometry. Let's create the coarsest level of geometry first. Looking at the xy-plot of the system (below), we see that we can roughly divide the geometry radially to four parts:

Fuel lattice and grid plates (for R < 26 cm).
Water surrounding the fuel lattice and grid plates for (26 cm < R < 30 cm).
Graphite reflector for (30 cm < R < 60 cm).
Water surrounding the graphite reflector for (60 cm < R < 100 cm).

We'll first create this radial division of the model to four parts and later work on the finer details. Start by creating an empty file called reactorpool and typing or copying the surface definitions below to the file. These are the radial limiting surfaces for the four regions.

/******** Radial boundaries of the core **************/

% --- Outer radius of the support plates and core

surf sCYL1 cylz 0.0 0.0 26

% --- Inner radius of the graphite reflector

surf sCYL2 cylz 0.0 0.0 30

% --- Outer radius of the graphite reflector

surf sCYL3 cylz 0.0 0.0 60

% --- Outer radius of the geometry

surf sCYL4 cylz 0.0 0.0 100

We'll define the first five geometry cells as follows (add these to the reactorpool-file):

/******** Radial cells of the reactor ****************/

% --- Notice that these cells are part of the universe "reactor"

cell cRadialCore     reactor water      -sCYL1
cell cRadialWater1   reactor water       sCYL1 -sCYL2
cell cRadialGraphite reactor graphite    sCYL2 -sCYL3
cell cRadialWater2   reactor water       sCYL3 -sCYL4
cell cRadialOutside  reactor outside     sCYL4

You should notice that these cells are defined as a part of an universe called reactor instead of the base universe 0. This means that we can modify our main input file (the reactor file) and fill the cell cIN (that previously contained water) with this reactor universe:

% --- Cell cIN is now filled with reactor    

cell cIN  0 fill reactor -sCUBE

We'll still need to link the new file reactorpool to our main input by adding the following lines to some part of it

 % --- Link the reactorpool file to this input

include "reactorpool"

Your reactor and reactorpool files should now look more or less like the ones below:

reactor

 % --- Research reactor input for Serpent tutorial

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% We'll start from a simple water geometry %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% --- Our reactor model will fit inside a cubic surface with an edge length of 100 cm

surf sCUBE cube 0.0 0.0 0.0 100.0

% --- Cell cIN is filled with the universe "reactor"

cell cIN  0 fill reactor -sCUBE

% --- Cell cOUT is defined as an outside cell

cell cOUT 0 outside       sCUBE

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Link additional input files here %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% --- Link the materials file to this input

include "materials"

% --- Link the reactorpool file to this input

include "reactorpool"

/******************
 * Run parameters *
 ******************/

% --- Neutron population: 10000 neutrons per cycle, 100 active / 50 inactive cycles

set pop 10000 100 50

% --- Geometry plots

% --- XY-plot

plot 3 200 200 0 -100 100 -100 100

% --- XZ-plot

plot 2 200 200 0 -100 100 -100 100

reactorpool

/******** Radial boundaries of the reactor ***********/

% --- Outer radius of the support plates and core

surf sCYL1 cylz 0.0 0.0 26

% --- Inner radius of the graphite reflector

surf sCYL2 cylz 0.0 0.0 30

% --- Outer radius of the graphite reflector

surf sCYL3 cylz 0.0 0.0 60

% --- Outer radius of the geometry

surf sCYL4 cylz 0.0 0.0 100

/******** Radial cells of the reactor ****************/

% --- Notice that these cells are part of the universe "reactor"

cell cRadialCore     reactor water      -sCYL1
cell cRadialWater1   reactor water       sCYL1 -sCYL2
cell cRadialGraphite reactor graphite    sCYL2 -sCYL3
cell cRadialWater2   reactor water       sCYL3 -sCYL4
cell cRadialOutside  reactor outside     sCYL4

If you plot the geometry again with

sss2 -plot reactor

you can now see that the radial reflector is in place:

Adding axial boundaries

Our reactor model is still infinite axially. Our water height should be 200 cm and our graphite reflector height should be 100 cm. We'll need to add some limiting surfaces to our reactorpool file

/******** Axial boundaries of the reactor ************/

% --- Bottom of geometry model

surf sModelBot    pz -100

% --- Top of geometry model

surf sModelTop    pz  100

% --- Bottom of graphite reflector

surf sReflBot     pz  -50

% --- Top of graphite reflector

surf sReflTop     pz   50

We'll need to use these surfaces to limit our existing cells axially. What's more we'll need to divide our cRadialGraphite cell axially into three cells that contain (from bottom to top) water, graphite and water. We'll also need to add new outside cells below and above our geometry. We'll modify our cell definitions to

/******** Radial cells of the reactor ****************/

% --- Notice that these cells are part of the universe "reactor"

cell cRadialCore         reactor water      -sCYL1        sModelBot -sModelTop
cell cRadialWater1       reactor water       sCYL1 -sCYL2 sModelBot -sModelTop
cell cRadialReflectorBot reactor water       sCYL2 -sCYL3 sModelBot -sReflBot
cell cRadialReflectorMid reactor graphite    sCYL2 -sCYL3 sReflBot  -sReflTop
cell cRadialReflectorTop reactor water       sCYL2 -sCYL3 sReflTop  -sModelTop
cell cRadialWater2       reactor water       sCYL3 -sCYL4 sModelBot -sModelTop
cell cRadialOutside1     reactor outside     sCYL4
cell cRadialOutside2     reactor outside    -sCYL4       -sModelBot
cell cRadialOutside3     reactor outside    -sCYL4        sModelTop

We can plot the geometry again to see that the graphite reflector is now axially limited:

Creating a 3D fuel rod model

The geometry is lacking the fuel rod lattice including the control rods and support grids.

We'll start the work on the details by creating a 3D model for the fuel rod. Let's look at what we are trying to achieve:

We have previously used the pin definition for creating two dimensional fuel rod models. Here we need to create a three dimensional structure, with different materials at different axial heights. We can do this by creating multiple 2D pin definitions and stacking them on top of each other vertically. The axial regions of the fuel rod model are (from bottom to top):

Water below the rod.
Plug region in grid: Cladding plug surrounded by water surrounded by stainless steel plate.
Plug region: Cladding plug surrounded by water.
Fuel region: Fuel pellet surrounded by a gas gap surrounded by cladding surrounded by water.
Plug region: Cladding plug surrounded by water.
Plug region in grid: Cladding plug surrounded by water surrounded by stainless steel plate.
Water above the rod.

There are only three different parts that we'll need to use the pin definitions for. Create a new file called fuelrod and add the following pin-definitions in it:

% --- Pin definitions needed for fuel rods

% --- Fuel part

pin pFuel
fuel       0.3975
void       0.4125
Zircaloy4  0.4750
water

% --- End plug in water

pin pPlug
Zircaloy4  0.4750
water

% --- End plug in support grid

pin pPlugInSteel
Zircaloy4  0.4750
water      0.4850
ssteel

In order to stack them vertically we'll need to define the limiting axial planes first. The planes should be

The bottom of lower grid.
The top of lower grid.
The bottom of the active fuel part.
The top of the active fuel part.
The bottom of upper grid.
The top of upper grid
The top of fuel rod.

We'll add the following surface definitions to the fuelrod file:

/***** Axial surfaces for fuel rods ***********/

% --- Bottom of the lower plate and fuel rods

surf sLowerBot pz -37.0

% --- Top of the lower plate

surf sLowerTop pz -35.0

% --- Bottom of the active fuel

surf sFuelBot  pz -25.0

% --- Top of the active fuel

surf sFuelTop  pz 25.0

% --- Bottom of the upper grid plate

surf sUpperBot pz 30.0

% --- Top of the upper grid plate

surf sUpperTop pz 32.0

% --- Top of the fuel rods

surf sRodTop   pz 35.0

Now we can use the pin definitions and the surface definitions to create vertically stacked cells that make up the 3D fuel rod model. We'll put these cells into an universe that we'll call F. Add the following cell definitions to your fuelrod file:

/***** Vertical layers (cells) for fuel rod ****/

% --- 3D universe for fuel pins
%     These cells are part of an universe "F"

cell cFP0 F water                        -sLowerBot
cell cFP1 F fill pPlugInSteel  sLowerBot -sLowerTop
cell cFP2 F fill pPlug         sLowerTop -sFuelBot
cell cFP3 F fill pFuel         sFuelBot  -sFuelTop
cell cFP4 F fill pPlug         sFuelTop  -sUpperBot
cell cFP5 F fill pPlugInSteel  sUpperBot -sUpperTop
cell cFP6 F fill pPlug         sUpperTop -sRodTop
cell cFP7 F water              sRodTop

Now we'll still need to link the fuelrod file to our main input. Add the following lines to the reactor file:

% --- Link the fuelrod file to this input

include "fuelrod"

We can proceed to plot our fuel rod model to check if we managed to create it properly. In order to plot it we will switch out the reactor universe from cell cIN and put the newly created fuel rod universe F in that cell instead (modification should be done to the reactor file:

% --- Cell cIN is now filled with the universe "F"

cell cIN  0 fill F -sCUBE

We can fill that cell with the reactor universe again in the future, but now we'll simply use it for plotting the fuel rod model. We should also modify our plot-commands in the reactor file to better capture the fuel rod in our plots:

% --- XY-plot

plot 3 200 200 0 -1 1 -1 1

% --- XZ-plot

plot 2 100 400 0 -1 1 -50 50

Plotting the geometry now with

sss2 -plot reactor

will yield the plots of the fuel rod geometry:

Creating the fuel pin lattice

Next we can either go on and create 3D models for the control rods and the empty lattice positions or create the lattice for the active core region.

Here we'll first create the lattice for the core and fill it with fuel rods and replace some of the fuel rods with control rods and empty lattice positions later.

Based on the fact that the core region has a diameter of 52 cm and the fuel rod pitch in the core lattice is 1.8 cm we'll need 52/1.8 ≈ 29 lattice elements to cover the region. We'll thus create a 29 by 29 lattice, that we'll currently fill with fuel rods, i.e. we'll put F for each lattice position. Create a new file called core and copy the lattice definition below to it

% --- Pin lattice definition, name of the lattice "core"
%     Lattice type 1 (square lattice)
%     Lattice centered at 0.0 0.0
%     29 x 29 lattice elements
%     Lattice pitch 1.80 cm

lat core 1 0.0 0.0 29 29 1.8
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F

F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F

F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F
F F F F F F F F F F F F F F  F  F F F F F F F F F F F F F F

We have now defined an universe "core" that consists of 29x29 fuel pins. We can plot this universe by linking it to the main reactor input file

% --- Link the core file to this input

include "core"

and filling the cell cIN this time with the universe core

% --- Cell cIN is filled with the universe "core"

cell cIN  0 fill core -sCUBE

We can modify the plot commands again to focus the plot on the correct region. We'll also make the plots slightly larger and add a second xy-plot at the level of the lower grid plate:

% --- XY-plot at the level of axial midplane

plot 3 500 500   0 -30 30 -30 30

% --- XY-plot at the level of lower grid

plot 3 500 500 -36 -30 30 -30 30

% --- XZ-plot

plot 2 500 667   0 -30 30 -40 40

Plotting the geometry now with

sss2 -plot reactor

will produce some geometry errors:

Plotting geometry:

   0% complete
Geometry errors in plot reactor_geom1.png (no cell).
  33% complete
Geometry errors in plot reactor_geom2.png (no cell).
  67% complete
Geometry errors in plot reactor_geom3.png (no cell).
 100% complete

The following three plots are produced:

The geometry errors (shown in green in the plots) mean that the areas outside the 29x29 fuel pin lattice do not have any cell defined to them so Serpent does not know which material should be there. This will not worry us because the 29x29 fuel pin lattice will go inside the graphite reflector and there will be some surroundings defined for the lattice at that point.

That said, let's put the fuel rod lattice in its place.

Setting the fuel pin lattice into the reactor

When we created our reactorpool input file and built the rough radial structure of our reactor we filled the center part of the reactor, where the active core should be, with water. This was the cell cRadialCore. Now we will fill that cell with the newly prepared universe core. So we'll edit the cell list in the reactorpool file:

/******** Radial cells of the reactor ****************/

% --- Notice that these cells are part of the universe "reactor"

cell cRadialCore         reactor fill core  -sCYL1        sModelBot -sModelTop
cell cRadialWater1       reactor water       sCYL1 -sCYL2 sModelBot -sModelTop
cell cRadialReflectorBot reactor water       sCYL2 -sCYL3 sModelBot -sReflBot
cell cRadialReflectorMid reactor graphite    sCYL2 -sCYL3 sReflBot  -sReflTop
cell cRadialReflectorTop reactor water       sCYL2 -sCYL3 sReflTop  -sModelTop
cell cRadialWater2       reactor water       sCYL3 -sCYL4 sModelBot -sModelTop
cell cRadialOutside1     reactor outside     sCYL4
cell cRadialOutside2     reactor outside    -sCYL4       -sModelBot
cell cRadialOutside3     reactor outside    -sCYL4        sModelTop

As we want to plot our reactor again, we'll fill the cell cIN in the main input file (reactor) with the universe reactor again:

% --- Cell cIN is filled with the universe "reactor"

cell cIN  0 fill reactor -sCUBE

We can tune the plot-commands a bit again to see both the whole reactor and a zoomed in pictures of the core:

% --- XY-plot of reactor, axial midplane

plot 3 500 500   0 -100 100 -100 100

% --- XY-plot of core, axial midplane

plot 3 500 500   0 -30 30 -30 30

% --- XY-plot of core, level of lower grid

plot 3 500 500 -36 -30 30 -30 30

% --- XZ-plot

plot 2 500 667   0 -30 30 -40 40

The reactor is definitely looking better and there are no more "No cell" geometry errors. There are fuel rods in the core and the lower and upper grid plates are in place.

However, there are still some problems with the model:

There are too many fuel rods, which is to say the empty lattice positions at the core periphery are missing.
There are no control rods.

Creating 3D models for empty lattice positions

In order to take out some of the fuel rods, we'll need a 3D model (universe) of an empty lattice position that we can apply at the correct positions of the core lattice. Let's look at an xz-cut of how an empty lattice position should look like:

There are only 5 axial layers for the empty lattice position:

Water below lower grid.
Water inside the hole in lower grid.
Water between grids.
Water inside the hole in upper grid.
Water above upper grid.

As three of the layers are filled simply with water, we'll need pin definitions only for the other two. As the two grids are identical, one pin definition will be enough. Create an empty file with the name emptyposition and add the following pin definition there:

% --- Pin definitions needed for empty positions

% --- Empty lattice position at grid

pin pHoleInSteel
water      0.4850
ssteel

We don't need additional surface definitions for the empty lattice positions as we defined the axial planes of the grids already for the fuel rod model. Instead, we can simply create the vertical stack of the different axial layers in the empty lattice position model:

/***** Vertical layers (cells) for empty position ****/

% --- 3D universe for empty lattice positions
%     These cells are part of an universe "_"

cell cEP0 _ water                        -sLowerBot
cell cEP1 _ fill pHoleInSteel  sLowerBot -sLowerTop
cell cEP2 _ water              sLowerTop -sUpperBot
cell cEP3 _ fill pHoleInSteel  sUpperBot -sUpperTop
cell cEP4 _ water              sUpperTop

We'll name the universe "_" (underscore) for reasons that will soon become obvious. Now we can link the emptyposition file to the main input (reactor):

% --- Link the emptyposition file to this input

include "emptyposition"

Finally we can replace the additional fuel rods F in the lattice core (in file core) with the newly created universe for empty lattice positions _:

% --- Pin lattice definition, name of the lattice "core"
%     Lattice type 1 (square lattice)
%     Lattice centered at 0.0 0.0
%     29 x 29 lattice elements
%     Lattice pitch 1.80 cm
%     We'll utilize our knowledge of the 1/8 symmetry so that
%     we'll only have to type in 1/8th of the core

lat core 1 0.0 0.0 29 29 1.8
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F F _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F F F _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F F F _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F F _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

As the core is 1/8 symmetric, we can simply put in one eight of the core and tell Serpent to utilize a symmetry in the core universe to fill out the rest of the core. This relieves us from some work, although we do need to add the set usym definition to the core file:

% --- Tell Serpent to apply a symmetry to the lattice "core"
%     Symmetry axis is the z-axis (3)
%     Symmetry boundary condition is reflective (2)
%     Symmetry axis is located at coordinates (0.0 0.0)
%     Symmetry covers an angle starting from 270 degrees
%     and extending for 45 degrees

set usym core 3 2 0.0 0.0 270 45

We can now plot the geometry again with

sss2 -plot reactor

to obtain new plots from the reactor. Now we'll present just two of them here:

Now we have the correct shape for the fuel rod lattice (although we have still replaced the control rods with fuel rods) but there seem to be too many holes in the grid plate as the holes reach the edge of the grid plate. Instead of empty positions, we'll need to create models for positions in the grid-plate where there are no positions at all.

Plugging the extra holes in the grid plates

We'll create another 3D model (universe) that we can use for the lattice positions, where there should not be a hole in the grid plates. As this is a rather simple universe, we'll put it directly at the end of the core file instead of its own file:

% --- 3D universe for lattice positions without a hole

cell cSS0 x water                        -sLowerBot
cell cSS1 x ssteel             sLowerBot -sLowerTop
cell cSS2 x water              sLowerTop -sUpperBot
cell cSS3 x ssteel             sUpperBot -sUpperTop
cell cSS4 x water              sUpperTop

we can now replace some of the elements (the correct elements) at the core periphery with this new universe x:

% --- Pin lattice definition, name of the lattice "core"
%     Lattice type 1 (square lattice)
%     Lattice centered at 0.0 0.0
%     29 x 29 lattice elements
%     Lattice pitch 1.80 cm
%     We'll utilize our knowledge of the 1/8 symmetry so that
%     we'll only have to type in 1/8th of the core

lat core 1 0.0 0.0 29 29 1.8
_ _ _ _ _ _ _ _ _ _ _ _ _ _ x x x x x x x x x x x x x x x
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ x x x x x x x x x _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F _ _ _ x x x x x x _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F _ _ x x x _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F F _ _ x _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F F F _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F F F _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F F _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

When we plot the geometry again, we can see that the extra holes have been plugged:

We are still missing the control rods from the model. We shall build them in three phases:

Create a 3D guide tube model filled with water and put it to the core lattice.
Create a 3D control rod model and put it inside the guide tube.
Add an universe transformation to move the control rods up and down.

Creating a 3D guide tube model

As previously, it is a good idea to first look at the way an empty guide tube is supposed to look like:

The axial regions of the guide tube model are (from bottom to top):

Water below the bottom grid
Water surrounded by a guide tube surrounded by water surrounded by stainless steel plate.
Water surrounded by a guide tube surrounded by water.
Water surrounded by a guide tube surrounded by water surrounded by stainless steel plate.
Water surrounded by a guide tube surrounded by water.

We'll create a new empty file guidetube and add the required pin-definitions into the file

% --- Pin definitions needed for the guide tubes

% --- Guide tube in water

pin pGT
water       0.75
Zircaloy4   0.80
water

% --- Guide tube in support grid

pin pGTInSteel
water       0.75
Zircaloy4   0.80
water       0.85
ssteel

Again, we don't need to define any additional axial surfaces. Instead we can add the vertically stacked cell-definitions for the axial layers directly to the guidetube file:

/***** Vertical layers (cells) for guide tubes ****/

% --- 3D universe for guide tubes
%     These cells are part of an universe "c"

cell cGT0 c water                        -sLowerBot
cell cGT1 c fill pGTInSteel    sLowerBot -sLowerTop
cell cGT2 c fill pGT           sLowerTop -sUpperBot
cell cGT3 c fill pGTInSteel    sUpperBot -sUpperTop
cell cGT4 c fill pGT           sUpperTop

The guide tube is created to the universe c which we can set to its correct place in the core lattice (in file core):

% --- Pin lattice definition, name of the lattice "core"
%     Lattice type 1 (square lattice)
%     Lattice centered at 0.0 0.0
%     29 x 29 lattice elements
%     Lattice pitch 1.80 cm
%     We'll utilize our knowledge of the 1/8 symmetry so that
%     we'll only have to type in 1/8th of the core

lat core 1 0.0 0.0 29 29 1.8
_ _ _ _ _ _ _ _ _ _ _ _ _ _ x x x x x x x x x x x x x x x
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ x x x x x x x x x _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F _ _ _ x x x x x x _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F _ _ x x x _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F F _ _ x _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F F F _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F F F _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F F _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F F _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F F F _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F c _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F F _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F F _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F F _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ F _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

Now, after we include the guidetube file to the reactor file with

% --- Link the guidetube file to this input

include "guidetube"

we can add a second XZ-plot through the core at the position where two of the control rods should be

% --- XZ-plot, level of control rods

plot 2 500 667 7.2 -30 30 -40 40

Plotting the geometry again produces many plots, the most interesting of which are shown here:

We now see that the guide tubes are in place and they are only missing the control rods.

Creating a 3D control rod model

We'll go about creating the control rod model as we have done for the other 3D models. Here is the axial structure shown with a fully inserted control rod:

The control rods are made up by four vertical layers (from bottom to top):

Water below the control rod.
Stainless steel.
Boron carbide.
Stainless steel.

The control rods will furthermore be surrounded by a small ring of water and the guide tube, but as we already have a model for the water filled guide tubes, we don't have to create those as a part of the control rod model.

We'll create a new empty file with the name controlrod this time we do not need to add any pin-definitions. We will use the previously defined axial surfaces to create the control rod in its fully inserted position by the following cell definitions added to the controlrod file:

/***** Vertical layers (cells) for control rods ****/

% --- 3D universe for control rods
%     These cells are part of an universe "CRuni"

cell cCR0 CRuni water  -sLowerBot
cell cCR1 CRuni ssteel  sLowerBot  -sFuelBot
cell cCR2 CRuni B4C     sFuelBot   -sFuelTop
cell cCR3 CRuni ssteel  sFuelTop

We'll now need to insert these control rods into the guide tubes by dividing the water part in the middle of our guide tube pin-definitions (in file guidetube) into two parts: the one containing the control rod and the surrounding water ring. This can be done by simply adding a new innermost region to the correct pin definitions and filling that region with the newly made universe CRuni:

% --- Pin definitions needed for the guide tubes

% --- Guide tube in water

pin pGT
fill CRuni  0.60
water       0.75
Zircaloy4   0.80
water

% --- Guide tube in support grid

pin pGTInSteel
fill CRuni  0.60
water       0.75
Zircaloy4   0.80
water       0.85
ssteel

We'll still need to link the controlrod file to the main input (reactor file):

% --- Link the controlrod file to this input

include "controlrod"

Now we can plot the geometry again to see:

The control rods are now in place in their fully inserted position.

Moving the control rods

The last thing to add is a transformation that lets us move the control rods. We will use an universe transformation applied to the control rod universe 'CRuni so that we can move the control rods up and down without moving the guide tubes up and down. We'll add the transformation to our main input file to some easy to access place:

% --- Transformation for the control rod movement
%     The values given are transformations in (x, y, z)
%     Transformation of  0.0 means fully inserted.
%     Transformation of 25.0 means 50 %  inserted.
%     Transformation of 50.0 means fully withdrawn.
%     e.g.

trans u CRuni 0.0 0.0 25.0

If we now plot the geometry using this 25 cm upwards transformation we can see that the control rods are lifted by 25 cm:

We pay a price for applying the universe symmetry to the core lattice here in the fact that we cannot move the control rods individually.

If individual movement of the control rods would be required, we would need to build separate models for each control rod (and their guide tubes) and then we could apply separate universe transformations to each of the rods.

Running the model

Before we run our model, we'll do some cleanup: During the model development we used the cells cIN and cOUT at many points for filling sCUBE with different universes to plot them and verify are work. Now these two cells are a redundant layer of our geometry. We don't really need to close our reactor model into a box (sCUBE) as we already define the outside of our model in our reactorpool-file. We can thus remove this additional layer from our geometry. In order to do this, we'll first remove the following lines from our main input file (reactor):

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% We'll start from a simple water geometry %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% --- Our reactor model will fit inside a cubic surface with an edge length of 100 cm

surf sCUBE cube 0.0 0.0 0.0 100.0

% --- Cell cIN is now filled with the universe "reactor"

cell cIN  0 fill reactor -sCUBE

% --- Cell cOUT is defined as an outside cell

cell cOUT 0 outside       sCUBE

Second, we'll modify the cell definitions in the end of the file reactorpool from

% --- Notice that these cells are part of the universe "reactor"

cell cRadialCore         reactor fill core  -sCYL1        sModelBot -sModelTop
cell cRadialWater1       reactor water       sCYL1 -sCYL2 sModelBot -sModelTop
cell cRadialReflectorBot reactor water       sCYL2 -sCYL3 sModelBot -sReflBot
cell cRadialReflectorMid reactor graphite    sCYL2 -sCYL3 sReflBot  -sReflTop
cell cRadialReflectorTop reactor water       sCYL2 -sCYL3 sReflTop  -sModelTop
cell cRadialWater2       reactor water       sCYL3 -sCYL4 sModelBot -sModelTop
cell cRadialOutside1     reactor outside     sCYL4
cell cRadialOutside2     reactor outside    -sCYL4       -sModelBot
cell cRadialOutside3     reactor outside    -sCYL4        sModelTop

to

% --- Now these cells are part of the universe "0"

cell cRadialCore         0 fill core  -sCYL1        sModelBot -sModelTop
cell cRadialWater1       0 water       sCYL1 -sCYL2 sModelBot -sModelTop
cell cRadialReflectorBot 0 water       sCYL2 -sCYL3 sModelBot -sReflBot
cell cRadialReflectorMid 0 graphite    sCYL2 -sCYL3 sReflBot  -sReflTop
cell cRadialReflectorTop 0 water       sCYL2 -sCYL3 sReflTop  -sModelTop
cell cRadialWater2       0 water       sCYL3 -sCYL4 sModelBot -sModelTop
cell cRadialOutside1     0 outside     sCYL4
cell cRadialOutside2     0 outside    -sCYL4       -sModelBot
cell cRadialOutside3     0 outside    -sCYL4        sModelTop

This makes our reactor pool definition the highest universe in our model.

Now we can run our model by simply typing

sss2 [ -omp N ] reactor

Ideas for additional testing and tinkering in part 5

Part 6: Generating a set of group constants for a fuel assembly

Part 6 overview

In this part we will generate a set of homogenized two group constants for the fuel assembly that we used in the assembly burnup tutorial.

The original purpose of Serpent was the generation of homogenized group constants (sometimes improperly called simply homogenized cross sections) for reduced order solvers such as nodal diffusion codes. The idea in group constant generation is to calculate representative neutronics properties for a system (e.g. a fuel assembly) in a way that conserves physical reaction rates in the system. In essence the spatial variation inside the system is averaged out resulting in a single set of group constants for the whole system (spatial homogenization of the neutronics properties) in addition, the energy variation of the neutronics properties is averaged to an energy group structure (energy condensation of the neutronics properties).

Since the group constants (neutronics properties) of a system have a dependence on the nuclide compositions of the different materials in the system as well as their temperatures and densities, the group constants are typically generated in a wide range of conditions and parametrized to cover this range of conditions.

Serpent offers automated tools for such purposes and the variations in the system parameters are divided into

Historical variations that take into account conditions that persist for an extended period of time, such as moderator temperature and density, boron concentration and positioning of control rods. These conditions are reflected in depleted fuel compositions and thus in the generated group constants.
Branch variations that take into account momentary variations in operating conditions, such as fuel temperature, moderator density and temperature, boron concentration and insertion of control rods.

The historical variations are taken in account by depleting the fuel assembly separately with each set of historical conditions to produce nuclide compositions that can be then used to generate group constants. The branch variations are then covered by taking nuclide compositions corresponding to some historical conditions and generating group constants while momentarily changing the operating conditions to reflect the branch variation.

The exact history cases and branch variations that need to be calculated depend on the group constant model that is used in the reduced order solver (e.g. nodal diffusion code). As an example, for the ARES nodal diffusion code the history and branch variations required for pressurized water reactor modelling (excluding control rod variations) are shown below.

Part 6 variations

To keep the number of simulations reasonable, we'll consider here a much simpler group constant model that only considers the following variations:

Historical variations:
- Coolant temperature (and density).
Momentary variations
- Coolant temperature (and density).
- Fuel temperature.

For all variations we consider only two bounding values:

Low
High

Which gives us the following historical variations:

Historical variations
	Low value	High value
Coolant temperature (density)	555 K (0.76155 g/cm³)	595 K (0.67570 g/cm³)

And the following momentary variations:

Momentary variations
	Low value	High value
Coolant temperature (density)	555 K (0.76155 g/cm³)	595 K (0.67570 g/cm³)
Fuel temperature	600 K	1200 K

Part 6 base input

We'll base our input on the final input that we used for the assembly burnup calculation, except that we do not use the set mcvol card to calculate the depletion zone volumes each time Serpent is executed. Instead we'll define the volumes of the depletion zones by hand with the set mvol card.

Copy and paste the input below to a file named base on your computer.

Colors in the input correspond to:

Comments
Control words
Name definitions
Name references

Base input for group constant generation

% --- Simple 2D EPR assembly geometry burnup model for Serpent tutorial

/****************************
 * Link external files here *
 ****************************/

% --- Include material volumes from a separate file

include "./base.mvol"

/************************
 * Material definitions *
 ************************/

% --- 3.0 wt-% enriched UO2
%     Temperature is set to 950 K

mat fuelNoGad  -10.3070 tmp 950.0 rgb 255 255 150 burn 1
92235.09c       -0.02644492
92238.09c       -0.85505247
 8016.09c       -0.11850261

% --- 0.25 wt-% enriched UO2 with 8.0 wt-% of Gd2O3
%     Temperature is set to 950 K

mat fuelYesGad -10.3070 tmp 950.0 rgb 150 255 150 burn 1
92235.09c       -0.00202753
92238.09c       -0.80898345
 8016.09c       -0.11957908
64152.09c       -0.00013411
64154.09c       -0.00148108
64155.09c       -0.01012049
64156.09c       -0.01408805
64157.09c       -0.01083999
64158.09c       -0.01731511
64160.09c       -0.01543111

% --- Cladding material Zircaloy-4
%     [Composition from PNNL-15870, Rev. 1]

mat Zircaloy4 -6.56000E+00 tmp 610
 8016.03c  -1.19276E-03
24050.03c  -4.16117E-05
24052.03c  -8.34483E-04
24053.03c  -9.64457E-05
24054.03c  -2.44600E-05
26054.03c  -1.12572E-04
26056.03c  -1.83252E-03
26057.03c  -4.30778E-05
26058.03c  -5.83334E-06
40090.03c  -4.97862E-01
40091.03c  -1.09780E-01
40092.03c  -1.69646E-01
40094.03c  -1.75665E-01
40096.03c  -2.89038E-02
50112.03c  -1.27604E-04
50114.03c  -8.83732E-05
50115.03c  -4.59255E-05
50116.03c  -1.98105E-03
50117.03c  -1.05543E-03
50118.03c  -3.35688E-03
50119.03c  -1.20069E-03
50120.03c  -4.59220E-03
50122.03c  -6.63497E-04
50124.03c  -8.43355E-04

% --- Coolant is water with 650 ppm soluble boric acid added
%     The temperature of water is 583 K
%     Density is calculated based on a pressure of 15.5 MPa
%     Hydrogen is flagged as a bound scatterer with the "moder"-card

mat water -0.70602 tmp 583 moder lwtr 1001 rgb 200 200 255
O-16.03c   3.330861e-01
H-1.03c    6.663259e-01
B-10.03c   7.186970e-05
B-11.03c   2.892846e-04

% --- Define thermal scattering libraries associated with hydrogen in light water
%     As there are no readymade thermal scattering libraries for 583 K
%     We will tell Serpent to interpolate using two bounding libraries:
%     -lwj3.11t (H-1 in light water at 574 K)
%     -lwj3.13t (H-1 in light water at 624 K)
%     See also: https://serpent.vtt.fi/download/SSS_THERMAL.pdf

therm lwtr 583 lwj3.11t lwj3.13t

/************************
 * Geometry definitions *
 ************************/

% --- Normal fuel rod (no gadolinia in fuel)

pin FF
fuelNoGad  0.3975
void       0.4125
Zircaloy4  0.4750
water

% --- Gadolinium fuel rod

pin GG
fuelYesGad  0.3975
void        0.4125
Zircaloy4   0.4750
water

% --- Empty instrumentation thimble

pin ii
water       0.5725
Zircaloy4   0.6125
water

% --- Empty control rod channel

pin cc
water       0.5725
Zircaloy4   0.6125
water

% --- Empty lattice position (just water)

pin ww
water

% --- Pin lattice definition, name of the lattice "lat1"
%     Lattice type 1 (square lattice)
%     Lattice centered at 0.0 0.0
%     19 x 19 lattice elements (17x17 fuel rods + 1 layer of water)
%     Lattice pitch 1.26 cm
%     We'll utilize our knowledge of the 1/8 symmetry so that
%     we'll only have to type in 1/8th of the assembly

lat lat1 1 0.0 0.0 19 19 1.26
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww FF FF FF FF FF FF FF FF FF ww
ww ww ww ww ww ww ww ww ww FF FF FF FF FF FF FF FF ww ww
ww ww ww ww ww ww ww ww ww cc FF FF cc FF FF GG ww ww ww
ww ww ww ww ww ww ww ww ww FF GG FF FF FF cc ww ww ww ww
ww ww ww ww ww ww ww ww ww FF FF FF FF GG ww ww ww ww ww
ww ww ww ww ww ww ww ww ww cc FF FF cc ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww FF FF GG ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww FF FF ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ii ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww
ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww ww

% --- Tell Serpent to apply a symmetry to the lattice "lat1"
%     Symmetry axis is the z-axis (3)
%     Symmetry boundary condition is reflective (2)
%     Symmetry axis is located at coordinates (0.0 0.0)
%     Symmetry covers an angle starting from 270 degrees
%     and extending for 45 degrees

set usym lat1 3 2 0.0 0.0 270 45

% --- A square surface around the fuel assembly

surf s1 sqc  0.0 0.0 10.752

% --- Cell c1 belongs to the base universe 0, is filled with the lattice lat1
%     and covers everything inside surface s1

cell c1 0 fill lat1     -s1

% --- Cell c2 belongs to the base universe 0, is defined as an "outside" cell
%     and covers everything outside surface s1

cell c2 0 outside        s1

/******************
 * Run parameters *
 ******************/

% --- Assembly linear power is 420 kW

set power 42000

% --- Boundary condition (1 = black, 2 = reflective, 3 = periodic)

set bc 2

% --- Neutron population: 5000 neutrons per cycle, 100 active / 20 inactive cycles

set pop 5000 100 20

% --- XY-plot (3), which is 700 by 700 pixels and covers the whole geometry

plot 3 700 700

% --- XY-meshplot (3), which is 700 by 700 pixels and covers the whole geometry

mesh 3 700 700

/***************************************
 * Settings for the burnup calculation *
 ***************************************/

% --- Burnup points for the burnup calculation (in MWd/kgU)
%     Too long intervals between the burnup points will decrease the
%     accuracy of the burnup calculation, especially during the burn-out 
%     of burnable absorber 

dep butot 0.1  0.5  1  3  5  7  9  11  13  15  17  19

% --- Material division for burnup calculation
%     Treat different pins of fuelNoGad as separate depletion zones (sep 1)

div fuelNoGad  sep 1

% --- Material division for burnup calculation
%     Treat different pins of fuelYesGad as separate depletion zones (sep 1)
%     additionally divide each of those fuel pellets into 10 equal volume rings
%     between radial coordinates of 0.0 and 0.3975

div fuelYesGad sep 1 subr 10 0.0 0.3975

% --- Nuclide inventory: these nuclides will be included in the
%     depletion output file burn_dep.m. The list can be changed
%     after the simulation has concluded if needed. Then you can run
%     sss2 -rdep burn
%     which will make Serpent re-read the inventory and re-produce the
%     depletion output file.

set inventory
 922350
 942390
 641550
 641570

% --- Use predictor corrector method for the depletion solution
%     leli: Linear extrapolation on predictor
%           Linear interpolation on corrector
%     10 10: 10 substeps on predictor, 10 substeps on corrector

set pcc leli 10 10

% --- Decay data library needs to be specified for burnup calculations

set declib "sss_jeff31.dec"

% --- Neutron induced fission yield library needs to be specified for
%     burnup calculations

set nfylib "sss_jeff31.nfy"

% --- Reduce unionized energy grid size in order to save some memory
%     Use grid thinning with 5e-5 reconstruction tolerance between
%     1e-9 and 15 MeV.

set egrid 5e-5 1e-9 15.0

Additionally, you will need to create a file named base.mvol and copy the following contents to the file

Material volumes for group constant generation

% --- Material volumes:

set mvol

fuelNoGad  35 1.98557E+00
fuelNoGad  34 1.98557E+00
fuelNoGad  33 3.97113E+00
fuelNoGad  32 1.98557E+00
fuelNoGad  31 3.97113E+00
fuelNoGad  30 3.97113E+00
fuelNoGad  29 3.97113E+00
fuelNoGad  28 3.97113E+00
fuelNoGad  27 3.97113E+00
fuelNoGad  26 1.98557E+00
fuelNoGad  25 3.97113E+00
fuelNoGad  24 3.97113E+00
fuelNoGad  23 3.97113E+00
fuelNoGad  22 1.98557E+00
fuelNoGad  21 3.97113E+00
fuelNoGad  20 3.97113E+00
fuelNoGad  19 3.97113E+00
fuelNoGad  18 3.97113E+00
fuelNoGad  17 1.98557E+00
fuelNoGad  16 3.97113E+00
fuelNoGad  15 3.97113E+00
fuelNoGad  14 3.97113E+00
fuelNoGad  13 3.97113E+00
fuelNoGad  12 3.97113E+00
fuelNoGad  11 3.97113E+00
fuelNoGad  10 1.98557E+00
fuelNoGad   9 1.98557E+00
fuelNoGad   8 3.97113E+00
fuelNoGad   7 3.97113E+00
fuelNoGad   6 3.97113E+00
fuelNoGad   5 3.97113E+00
fuelNoGad   4 3.97113E+00
fuelNoGad   3 3.97113E+00
fuelNoGad   2 3.97113E+00
fuelNoGad   1 1.98557E+00
fuelYesGad  40 1.98557E-01
fuelYesGad  39 1.98557E-01
fuelYesGad  38 1.98557E-01
fuelYesGad  37 1.98557E-01
fuelYesGad  36 1.98557E-01
fuelYesGad  35 1.98557E-01
fuelYesGad  34 1.98557E-01
fuelYesGad  33 1.98557E-01
fuelYesGad  32 1.98557E-01
fuelYesGad  31 1.98557E-01
fuelYesGad  30 1.98557E-01
fuelYesGad  29 1.98557E-01
fuelYesGad  28 1.98557E-01
fuelYesGad  27 1.98557E-01
fuelYesGad  26 1.98557E-01
fuelYesGad  25 1.98557E-01
fuelYesGad  24 1.98557E-01
fuelYesGad  23 1.98557E-01
fuelYesGad  22 1.98557E-01
fuelYesGad  21 1.98557E-01
fuelYesGad  20 3.97113E-01
fuelYesGad  19 3.97113E-01
fuelYesGad  18 3.97113E-01
fuelYesGad  17 3.97113E-01
fuelYesGad  16 3.97113E-01
fuelYesGad  15 3.97113E-01
fuelYesGad  14 3.97113E-01
fuelYesGad  13 3.97113E-01
fuelYesGad  12 3.97113E-01
fuelYesGad  11 3.97113E-01
fuelYesGad  10 1.98557E-01
fuelYesGad   9 1.98557E-01
fuelYesGad   8 1.98557E-01
fuelYesGad   7 1.98557E-01
fuelYesGad   6 1.98557E-01
fuelYesGad   5 1.98557E-01
fuelYesGad   4 1.98557E-01
fuelYesGad   3 1.98557E-01
fuelYesGad   2 1.98557E-01
fuelYesGad   1 1.98557E-01

Setting up the historical variations

In order to run the two historical variations we need to create separate inputs for each of the variation cases. The only real difference in input is the water temperature and density in the calculation. It is perhaps easiest to define the water material in two files (one with low temperature and one with high) and include only one of them in the main input.

So, we'll create two new files:

water_low.inc

% --- Coolant is water with 650 ppm soluble boric acid added
%     The temperature of water is 555 K (low temperature state point)
%     Density is calculated based on a pressure of 15.5 MPa
%     Hydrogen is flagged as a bound scatterer with the "moder"-card

mat water -0.76105 tmp 555 moder lwtr 1001 rgb 200 200 255
O-16.03c   3.330861e-01
H-1.03c    6.663259e-01
B-10.03c   7.186970e-05
B-11.03c   2.892846e-04

% --- Define thermal scattering libraries associated with hydrogen in light water
%     As there are no readymade thermal scattering libraries for 555 K
%     We will tell Serpent to interpolate using two bounding libraries:
%     -lwj3.09t (H-1 in light water at 524 K)
%     -lwj3.11t (H-1 in light water at 574 K)
%     See also: https://serpent.vtt.fi/download/SSS_THERMAL.pdf

therm lwtr 555 lwj3.09t lwj3.11t

water_high.inc

% --- Coolant is water with 650 ppm soluble boric acid added
%     The temperature of water is 595 K (high temperature state point)
%     Density is calculated based on a pressure of 15.5 MPa
%     Hydrogen is flagged as a bound scatterer with the "moder"-card

mat water -0.67570 tmp 595 moder lwtr 1001 rgb 200 200 255
O-16.03c   3.330861e-01
H-1.03c    6.663259e-01
B-10.03c   7.186970e-05
B-11.03c   2.892846e-04

% --- Define thermal scattering libraries associated with hydrogen in light water
%     As there are no readymade thermal scattering libraries for 595 K
%     We will tell Serpent to interpolate using two bounding libraries:
%     -lwj3.11t (H-1 in light water at 574 K)
%     -lwj3.13t (H-1 in light water at 624 K)
%     See also: https://serpent.vtt.fi/download/SSS_THERMAL.pdf

therm lwtr 595 lwj3.11t lwj3.13t

Additionally, we'll need to remove the definition of the water material from the base-input and replace it with

% --- Include water composition from a file

include "./water_low.inc"

or

% --- Include water composition from a file

include "./water_high.inc"

It is a good idea to copy the base input file to two separate files (e.g. input_low and input_high) and include the correct water composition to each.

Setting up the branch variations

The branch variations can be set up using the branch and coef cards. This would be a good time to read through the detailed information on the branch types.

Create a new file branches.inc that you can write the branch definitions into.

As noted before, we will need to apply four different variations to the system:

Reduced fuel temperature.
Increased fuel temperature.
Reduced coolant temperature.
Increased coolant temperature.

We will create a separate branch definition for each of these variations. The coef card will then allow us to apply one or more of the branch variations at the same time. Let's start with the fuel temperature branches:

We'll name our fuel temperature branches as lowFuelTemperature and highFuelTemperature. Since we need to modify the temperature of some existing materials for the branch, we will use the stp option in the branch card to achieve this. The stp option takes as its argument, the name of the material whose temperature and/or density is modified, the new material density and the new material temperature. We need to remember to modify the temperatures of both fuel materials, the one with burnable gadolinium and the one without. The fuel temperature branches are quite simple to write:

% --- Fuel temperature branches:

%     We'll use the "stp" option in the branch card to modify the
%     temperature and density of the material.

branch lowFuelTemperature
stp fuelNoGad  -10.3070 600
stp fuelYesGad -10.3070 600
var TFU 600

branch highFuelTemperature
stp fuelNoGad  -10.3070 1200
stp fuelYesGad -10.3070 1200
var TFU 1200

Only the temperature of the fuel is different in these branches. The density is kept at the nominal value of 10.370 g/cm³. We have also used the var option for the branch card. The var option does not make any variations itself. Instead, it makes possible to pass a named variable (here TFU) to the group constant output along with an associated value (here 600 or 1200). This allows our post processing script to read in the value of TFU (i.e. the fuel temperature) that corresponds to each branch from the group constant output and we don't have to manually give that value to the post processing script. The names of the variables as well as their values can be freely chosen by the user.

The coolant temperature branches are not much more difficult than the fuel temperature ones. The only difference is that as our coolant contains a bound scatterer (hydrogen-1 in light water) that was associated with thermal scattering libraries in the material definition (with the moder option), we need to supply three additional parameters to the stp card. These options are

The name of therm card associated with the material.
Name of a data library at temperature below or equal to the given value.
Name of a data library at temperature above or equal to the given value.

Using this syntax, we can write our coolant temperature branches:

% --- Coolant temperature branches:

%     We'll use the "stp" option in the branch card to modify the
%     temperature and density of the material. Since the water material
%     has a thermal scattering library linked to it, we'll also provide
%     the correct bracketing thermal scattering libraries for the
%     branch temperature

branch lowCoolantTemperature
stp water -0.76105 555 lwtr lwj3.09t lwj3.11t
var TCO 555

branch highCoolantTemperature
stp water -0.67570 595 lwtr lwj3.11t lwj3.13t
var TCO 595

Here we again use the var option to pass the TCO 555 and TCO 595 information to the group constant output. Now we have defined all of our branch variations and the only thing remaining to do is to define the coefficient matrix that tells Serpent at which depletion points and branch variations the group constants are generated.

We will generate the group constants at five different burnups: 0, 1, 5, 11 and 19 MWd/kgU. These points must correspond to points in the burnup calculation as defined by the dep card in the main input. At each burnup point, we vary the fuel temperature to two values and the coolant temperature to two values. These variations can be thought to be independent of each other and to form a 2x2 matrix in a sense. Our coef card will thus become

% --- Coefficient matrix:
%     We have variations in two dimensions (fuel T, coolant T) for each depletion point:

coef   5   0 1 5 11 19
2   lowFuelTemperature highFuelTemperature
2   lowCoolantTemperature highCoolantTemperature

Here, the first line contains the coef card itself, the number of burnup points to generate the group constants at and a list of these burnup points. The burnup point definition is followed by the branch variations that are conducted at each point. The second line indicates that one dimension of our coefficient matrix consists of 2 variations, namely the branches lowFuelTemperature and highFuelTemperature. The third line defines our second dimension of the coefficient matrix, also consisting of 2 variations, the branches lowCoolantTemperature and highCoolantTemperature. The total number of variations at each point is 2x2=4.

You will still need to include the branches.inc file to your input_low and input_high files:

% --- Include branch definitions from a file

include "./branches.inc"

The finalized branches.inc file is shown below:

branches.inc

 
% --- Fuel temperature branches:

%     We'll use the "stp" option in the branch card to modify the
%     temperature and density of the material.

branch lowFuelTemperature
stp fuelNoGad  -10.3070 600
stp fuelYesGad -10.3070 600
var TFU 600

branch highFuelTemperature
stp fuelNoGad  -10.3070 1200
stp fuelYesGad -10.3070 1200
var TFU 1200

% --- Coolant temperature branches:

%     We'll use the "stp" option in the branch card to modify the
%     temperature and density of the material. Since the water material
%     has a thermal scattering library linked to it, we'll also provide
%     the correct bracketing thermal scattering libraries for the
%     branch temperature

branch lowCoolantTemperature
stp water -0.76105 555 lwtr lwj3.09t lwj3.11t
var TCO 555

branch highCoolantTemperature
stp water -0.67570 595 lwtr lwj3.11t lwj3.13t
var TCO 595

% --- Coefficient matrix:
%     We have variations in two dimensions (fuel T, coolant T) for each depletion point:

coef   5   0 1 5 11 19
2   lowFuelTemperature highFuelTemperature
2   lowCoolantTemperature highCoolantTemperature

Adding important options for group constant generation

We'll still need to specify some options that are important for group constant generation but can be ignored in other kinds of calculations.

The first thing we need to specify is the universe, in which the group constants are generated. This is set using the set gcu card. Here we can generate the group constants in the root universe (universe 0) as we are homogenizing everything over our whole system. In other cases, where the system that is to be homogenized is a part of some larger colorset, supercell or full core model, we might need to generate the group constants in some smaller universe. Now we can simply add

% --- Generate group constants in universe 0

set gcu 0

to our input files.

We'll also need to define the energy group structure into which the group constants will be calculated. This can be done with the set nfg card, which sets the few group structure (also called macro group structure) into which the group constants are condensed. We will be using the normal two-group structure with a boundary between the groups at 0.625 eV. We'll thus add the following definition to our main input files:

% --- Use default two group structure as the macro group structure

set nfg default2_ext

All of the pre-defined energy group structures are listed on a separate page but you could also define an energy group structure manually using the ene card.

Serpent uses a finer multi group (micro group) structure to store intermediate results for the group constants. The micro group structure is especially utilized when calculating the out-scattering diffusion coefficient or if the fundamental mode calculation (set fum) is switched on. To get reasonable results for the diffusion coefficient, we will use a pre-defined 70 group stucture using the set micro (as we are not using the fundamental calculation mode) input card:

% --- Use default 70 group structure as the micro group structure

set micro defaultmg_ext

The last option we will switch on is the calculation and use of an equilibrium xenon distribution. The ¹³⁵Xe isotope of xenon is an important short lived neutron absorbing nuclide produced by the decay of the fission product ¹³⁵I. Due to its importance as a neutron absorber and its tendency to quickly follow changes in neutron flux (i.e. power level), the nuclide concentration for ¹³⁵Xe is often solved separately from the general burnup problem. The equilibrium xenon calculation can be switched on using the set xenon input card. With the equilibrium xenon calculation switched on, Serpent calculates and updates the xenon-135 concentrations in each of the depletion zones already during the neutron transport assuming that the production and loss terms related to the nuclide concentration are in equilibrium (steady state). We'll switch on equilibrium xenon calculation for our inputs by adding the following lines:

% --- Calculate xenon-135 concentrations using the equilibrium xenon model

set xenon 1

Running the burnup calculation for the historical variations

Now we have set up both input_low and input_high for the calculation of the group constants. The two inputs include the correct coolant composition for the burnup calculation (historical coolant temperature) and both include the same branches as well as the same options for group constant generation.

We could now simply run the two cases with

sss2 -omp N input_low

and

sss2 -omp N input_high

where N stands for the number of parallel OpenMP threads we want to use to speed up the calculation.

Running the inputs in such a manner would

Run the burnup calculation generating restart files containing depleted nuclide compositions.
Run restart calculations that read the correct depleted compositions, apply the branch variations and generate the group constants at the burnup points and branch variations that we requested.

We can also run this in two parts, which is what we are going to do here. You can run the burnup calculation first by adding a -his argument to your command:

sss2 -omp N -his input_low

and

sss2 -omp N -his input_high

This should run the calculations. As we noticed in our earlier assembly burnup calculation, this part will take some time even though the neutron population we are using is much lower than what should be used in "real" calculations.

The simulations should produce similar output to our earlier assembly burnup calculation, but now we should get two additional output files:

input_low.wrk
input_high.wrk

These are binary files that contain the depleted fuel compositions that Serpent can use for the actual group constant generation with the branch variations.

Running the branch variations

When we have executed our burnup calculations and produced the restart files, we can run the branch calculations with the -coe command line argument:

sss2 -omp N -coe input_low

and

sss2 -omp N -coe input_high

Now Serpent will run separate simulations for each of our branch variations at each of the requested burnup points using depleted material compositions.

The output will be written in input_low.coe and input_high.coe in the format described on a separate page.

Post processing the group constant data

You can use the following OCTAVE/MATLAB script to read in all of the group constants in a file to arrays. If you save the script to the same folder as your output files, you should be able to open up OCTAVE/MATLAB in that folder and use the command (in OCTAVE/MATLAB):

run readGC.m

This will read in all of the group constant data into your OCTAVE/MATLAB workspace.

You can now try e.g. plotting some group constants (INF_ABS, INF_FISS, INF_DIFFCOEF) as a function of burnup and momentary or historical fuel and coolant temperatures.

OCTAVE script for reading in group constant data from Serpent .coe files. Save to readGC.m

files  = ["input_low.coe "; "input_high.coe"];
hisTCO = [555, 595];
momTFU = [600, 1200];
momTCO = [555, 595];

Nbu  = 5; ## Burnup points
Nhis = 2; ## Historical variations (coolant temperature)
Ntfu = 2; ## Momentary fuel temperature variations
Ntco = 2; ## Momentary coolant temperature variations
Ng   = 2; ## Energy groups

for Ihis = 1:1:2

  filename  = files(Ihis, :);
  curHISTCO = hisTCO(Ihis);

  ## Open the file

  file_as_text = fileread("./input_low.coe");

  ## Split file to lines

  lines = strsplit(file_as_text, "\n");

  ## Initialize

  i = 1;
  Ntot = 1;
  processed = 0;

  Itfu = 0;
  Itco = 0;

  ## Loop over COE-points

  while processed < Ntot

    ## Get the header for this branch
    ## See
    ## https://serpent.vtt.fi/mediawiki/index.php/Automated_burnup_sequence#Output_format

    ## Get next line as string

    line = lines{i}; i = i + 1;

    ## Split the line at empty spaces to tokens

    tokens = strsplit(line, " ");

    ## Get the tokens from the first header lin

    Itot = str2num(tokens{1});
    Ntot = str2num(tokens{2});
    Icoe = str2num(tokens{3});
    Ncoe = str2num(tokens{4});
    Nuni = str2num(tokens{5});


    ##
    ##
    ##

    ## Get next line as string

    line = lines{i}; i = i + 1;

    ## Split the line at empty spaces to tokens

    tokens = strsplit(line, " ");

    ##
    ## Branch line
    ##

    ## .. We don't need the branch information

#####################################
#####################################
#####################################

    ## Get next line as string

    line = lines{i}; i = i + 1;

    ## Split the line at empty spaces to tokens

    tokens = strsplit(line, " ");

    ##
    ## Variables line
    ##

    Nvar = str2num(tokens{1});

    for Ivar = 0:1:Nvar - 1
      varName = tokens{1 + Ivar*2 + 1};
      varVal  = tokens{1 + Ivar*2 + 2};

      if strcmp(varName, "TFU")
	curTFU = str2num(varVal);
      endif

      if strcmp(varName, "TCO")
	curTCO = str2num(varVal);
      endif
    endfor

#####################################
#####################################
#####################################

    ## Get next line as string

    line = lines{i}; i = i + 1;

    ## Split the line at empty spaces to tokens

    tokens = strsplit(line, " ");

    ##
    ## Burnup line
    ##

    ## Get current burnup and burnup index

    curBU = str2num(tokens{1});
    Ibu = str2num(tokens{2});

#####################################
#####################################
#####################################

    ## Get next line as string

    line = lines{i}; i = i + 1;

    ## Split the line at empty spaces to tokens

    tokens = strsplit(line, " ");

    ##
    ## Universe line
    ##

    ## Get number of group coefficients

    Ncoe = str2num(tokens{2});

#####################################
#####################################
#####################################

    ## Loop over group constants

    disp(["Processing group constants for burnup " ...
	    num2str(curBU) ", historical TCO of " num2str(curHISTCO) ...
	  " K "
	  "momentary TCO of " num2str(curTCO) " K and " ...
	  "fuel temperature of " num2str(curTFU) " K."])

    ## Get momentary branch indices

    Itfu = find(momTFU == curTFU);
    Itco = find(momTCO == curTCO);

    ## Loop over group constants

    for Icoe = 1:1:Ncoe

      ## Get next line as string

      line = lines{i}; i = i + 1;

      ## Split the line at empty spaces to tokens

      tokens = strsplit(line, " ");

      ##
      ## ... Process the group constant
      ##

      gcName = tokens{1};

      Ndata = str2num(tokens{2});

      if (Ndata > 0)
	command = [gcName "(" num2str(Ibu) ", " num2str(Ihis) ", " ...
			  num2str(Itfu) ", " num2str(Itco) ", :) = ["];

	for Idata = 1:1:Ndata
	  command = [command num2str(tokens{2 + Idata}) " "];
	endfor

	command = [command "];"];

	##disp(command);
	eval(command)
      endif
    endfor


    ## Increment the number of processed blocks

    processed = processed + 1;
  endwhile
endfor

Additional work

In addition to the default set of group constants, Serpent can calculate additional data that is often required by the reduced order solvers.

Generating fission poison data

Using the set poi input card.

Generating assembly discontinuity factors

Using the set adf input card.

Generating pin power form factors

Using the set ppw input card.

Applying a leakage correction

Using the set fum input card. A good micro-group structure (wms172_ext?). Set batching to 2. Using B1 in this example.

Final part: Options for real life calculations

This tutorial has tried to keep things as simple as possible, which means that some options that should be considered in production calculations have not been mentioned yet. This part tries to list several options that may be important to switch on when running calculations in the future.

Doppler broadening rejection correction

Using the set dbrc card.

Affects the sampling probabilities of elastic scattering reactions. Needs to be on to get correct results. It is switched off by default as that is the default also in MCNP. Requires zero Kelvin cross section data.

Reasonable default input:

set dbrc 0.1e-6 1e-3 92234.00c 92235.00c 92238.00c 94239.00c 94240.00c

Unresolved resonance probability table sampling

Using the set ures card.

Reasonable default input:

set ures 1

Energy grid thinning

References

^ Sengler, G., Fort, F., Schlosser, G., Lisdat, R., Stelletta, S. "EPR core design." Nucl. Eng. Des., 187 (1999), 79 – 119.

[Sengler-1] Sengler, G., Fort, F., Schlosser, G., Lisdat, R., Stelletta, S. "EPR core design." Nucl. Eng. Des., 187 (1999), 79 – 119.

[1]

Tutorial

Contents

Prerequisite

Part 1: Infinite homogeneous system

Part 1 overview

Part 1 input

Running the input for the infinite system

Finding the critical uranium enrichment

Calculating the flux energy spectrum

Testing the effect of added moderation

Ideas for additional testing and tinkering in part 1

Part 2: A 2D pin-cell (infinite lattice)

Part 2 overview

Part 2 input

Plotting the input

Running the input

Setting up additional mesh-plots

Calculating radial reaction rate distributions in the fuel pellet

Ideas for additional testing and tinkering in part 2

Part 3: A 2D assembly model (infinite lattice)

Part 3 overview

Part 3 input

Running the input for the assembly geometry

Testing the power feedback effects in the assembly

Changing the fuel temperature

Changing the water temperature

Changing the water density

Calculating the k-eff for the modified system

Calculating the pin power distribution

Ideas for additional testing and tinkering in part 3

Part 4: Assembly burnup calculation

Part 4 overview

Part 4 input

Depletion zone division

Specifying material volumes

Running the burnup calculation

Changes in assembly due to burnup

Ideas for additional testing and tinkering in part 4

Part 5: A 3D research reactor model

Part 5 overview

Part 5 geometry details

Radial geometry

Axial geometry

Lattice and grid plate geometry

Fuel rod geometry

Control rod geometry

Part 5 material details

Building the Serpent model for the reactor

Initial input

Coarse radial model

Adding axial boundaries

Creating a 3D fuel rod model

Creating the fuel pin lattice

Setting the fuel pin lattice into the reactor

Creating 3D models for empty lattice positions

Plugging the extra holes in the grid plates

Creating a 3D guide tube model

Creating a 3D control rod model

Moving the control rods

Running the model

Ideas for additional testing and tinkering in part 5

Part 6: Generating a set of group constants for a fuel assembly

Part 6 overview

Part 6 variations

Part 6 base input

Setting up the historical variations

Setting up the branch variations

Adding important options for group constant generation

Running the burnup calculation for the historical variations

Running the branch variations

Post processing the group constant data

Additional work

Generating fission poison data

Generating assembly discontinuity factors

Generating pin power form factors

Applying a leakage correction

Final part: Options for real life calculations

Doppler broadening rejection correction

Unresolved resonance probability table sampling

Energy grid thinning