Mesh types

Mesh types

Each physical data field consists of values on a specific mesh. Whereas several mesh types should be supported by Cerberus, the individual solvers typically only need to support their own mesh types. This section describes the geometry of the different mesh types supported by Cerberus and the mesh-data (the ordered list of values exactly specifying the mesh) associated with each mesh type.

Type 1 — Structured regular Cartesian mesh

Structured regular Cartesian meshes (in Kraken) are 3D meshes that cover a cuboid volume ([x_min, x_max]*[y_min, y_max]*[z_min, z_max]) and have a fixed number of cells in the x-, y- and z-direction (N_x, N_y, N_z). The total number of cells is the product of the number of cells in each of the three coordinate directions. The size/spacing of the cells is constant, but can be different for the different directions.

The mesh data for structured Cartesian meshes is as follows

Data type/size	Data content (explanation)	Data content (example)	Notes
1*integer	Mesh type	1
	Information on mesh size
1*integer	Nx	2	Number of cells in X-direction.
1*integer	Ny	1	Number of cells in Y-direction.
1*integer	Nz	4	Number of cells in Z-direction.
	Information on mesh boundaries
2*float	xmin, xmax	-10.0, 10.0	The outer limits of the mesh.
2*float	ymin, ymax	-5.0, 5.0	The outer limits of the mesh.
2*float	zmin, zmax	0.0, 100.0	The outer limits of the mesh.

Default indexing

x runs fastest, then y and finally z slowest.

All indices increase from minimum coordinate to maximum coordinate.

Type 2 — Structured irregular Cartesian mesh

Structured Cartesian meshes (in Kraken) are 3D meshes that cover a cuboid volume ([x_min, x_max]*[y_min, y_max]*[z_min, z_max]) and have a fixed number of cells in the x-, y- and z-direction (N_x, N_y, N_z). The total number of cells is the product of the number of cells in each of the three coordinate directions. For the irregular version, the size/spacing of the cells need not be constant.

The mesh data for structured irregular Cartesian meshes is as follows

Data type/size	Data content (explanation)	Data content (example)	Notes
1*integer	Mesh type	2
	Information on mesh size
1*integer	Nx	2	Number of cells in X-direction.
1*integer	Ny	1	Number of cells in Y-direction.
1*integer	Nz	4	Number of cells in Z-direction.
	Information on mesh boundaries
(Nx+1)*float	x0, x1, ..., xNx+1	-10.0, -5.0, 10.0	The cell boundaries in X-direction.
(Ny+1)*float	y0, y1, ..., yNy+1	-5.0, 5.0	The cell boundaries in Y-direction.
(Nz+1)*float	z0, z1, ..., zNz+1	0.0, 35.0, 50.0, 65.0, 100.0	The cell boundaries in Z-direction.

Default indexing

x runs fastest, then y and finally z slowest.

All indices increase from minimum coordinate to maximum coordinate.

Types 3-6 — Structured hexagonal meshes

Four different hexagonal meshes are currently supported (types 3-6). The different mesh types correspond to different orientations of the hexagons and to different choices of basis vectors.

The mesh data for all structured hexagonal meshes is the same:

Data type/size	Data content (explanation)	Data content (example)	Notes
1*integer	Mesh type	3
	Information on mesh size
1*integer	Nx	4	Number of cells in X-direction.
1*integer	Ny	4	Number of cells in Y-direction.
1*integer	Nz	4	Number of cells in Z-direction.
	Information on horizontal mesh geometry
2*float	x0, y0	0.0, 0.0	The horizontal centerpoint of the mesh.
1*float	pitch	0.236	The horizontal pitch between adjacent mesh cells.
	Information on axial boundaries
(Nz+1)*float	z0, z1, ..., zNz+1	0.0, 0.35, 0.50, 0.65, 1.0	The cell boundaries in Z-direction.

The following subsections show the base indexing in the different mesh types.

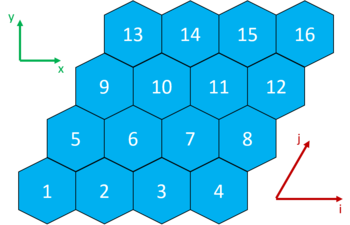
Type 3 — Structured x-type 60 degree hexagonal mesh

A single axial layer of the x-type (pointy top) hexagonal mesh with a 60 degree angle between the basis vectors is shown here:

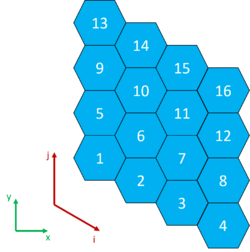
Type 4 — Structured y-type 60 degree hexagonal mesh

A single axial layer of the y-type (flat top) hexagonal mesh with a 60 degree angle between the basis vectors is shown here:

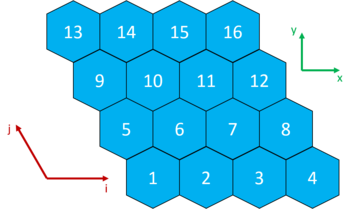
Type 5 — Structured x-type 120 degree hexagonal mesh

A single axial layer of the x-type (pointy top) hexagonal mesh with a 120 degree angle between the basis vectors is shown here:

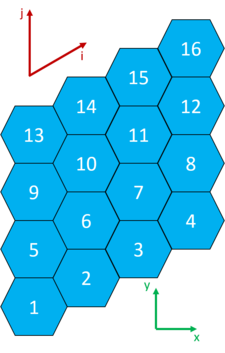
Type 6 — Structured y-type 120 degree hexagonal mesh

A single axial layer of the y-type (flat top) hexagonal mesh with a 120 degree angle between the basis vectors is shown here:

Type 7 — Structured cylindrical mesh

The mesh data for structured cylindrical meshes is as follows

Data type/size	Data content (explanation)	Data content (example)	Notes
1*integer	Mesh type	7
	Information on mesh size
1*integer	Nr	5	Number of radial cells.
1*integer	Nphi	1	Number of angular cells.
	Information on mesh boundaries
(Nr + 1)*float	r0, r1, r2, ...	0.0, 0.1e-2, 0.2e-2, 0.3e-2, 0.4e-2	The cell boundaries for the mesh in the radial direction.
(Nphi + 1)*float	phi0, phi1, phi2, ...	0, 360	The cell boundaries for the mesh in the angular direction (degrees, as in polar coordinates).

Default indexing

Radial indexing runs fastest and angular indexing slower.

Type 8 — Nested mesh

Data type/size	Data content (explanation)	Data content (example)	Notes
1*integer	Mesh type	8
1*integer	Nm	2	Number of nested meshes.
	Information on Nm nested meshes
1*integer	Mesh 1 type (top level)	1
	... The rest of the mesh 1 data.
	Mesh 2 type (second highest level)	1
	... The rest of the mesh 2 data.
	Mesh Nm type (lowest level)	1
	... The rest of the mesh Nm data.

Type 9 — List

The list mesh type does not have any clearly defined spatial structure. It may be useful for passing in data, for which the exact geometric configuration is irrelevant. When exactly to use a Field on a List mesh and when to use a Variable instead may be a matter of taste.

Data type/size	Data content (explanation)	Data content (example)	Notes
1*integer	Mesh type	9
1*integer	Nval	10	Number of values in the list.

Type 10 — Mixed nested mesh

The mixed nested mesh consists of a top level mesh (of any other mesh type) whose each cell may be filled with a sub-mesh of any kind.

Data type/size	Data content (explanation)	Data content (example)	Notes
1*integer	Mesh type	10
1*integer	Top mesh type	1	Would be structured regular Cartesian.
data type and size is dependent on top mesh type	... The rest of the top mesh data.	2 2 1 -20.0 20.0 -20.0 20.0 -100.0 100.0	Would be a 2x2x1 Cartesian mesh.
1*integer	Nm	3	Number of different sub-meshes in top mesh cells.
	Information on Nm sub-meshes
1*integer	Sub-mesh 1 type	1	Would be structured regular Cartesian.
data type and size is dependent on sub-mesh type	The rest of the sub-mesh 1 data.	2 2 1 -10.0 10.0 -10.0 10.0 -100.0 100.0	Would be a 2x2x1 Cartesian mesh.
1*integer	Sub-mesh 2 type	1	Would be structured regular Cartesian.
data type and size is dependent on sub-mesh type	The rest of the mesh 2 data.	1 1 1 -10.0 10.0 -10.0 10.0 -100.0 100.0	Would be a 1x1x1 Cartesian mesh.
1*integer	Mesh Nm type (lowest level)	1	Would be structured regular Cartesian.
data type and size is dependent on sub-mesh type	The rest of the sub-mesh Nm data.	3 3 1 -10.0 10.0 -10.0 10.0 -100.0 100.0	Would be a 3x3x3 Cartesian mesh.
Ntopc*integer	Index of sub-mesh in each cell of the top mesh.	1 2 3 1	Ntopc is the number of cells in the top mesh

Indexing array

Each of the mesh types described in the previous section have their own default indexing sometimes referred to as global indexing.

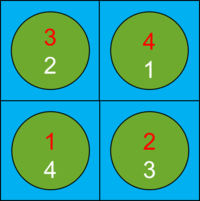
Sometimes the data accepted or provided by a solver may lie on a specific mesh type but follow an indexing that is different from this default. Consider the situation in the following figure:

The red numbers indicate the default indexing in this 2x2x1 regular Cartesian mesh. If our coupled solver would have the inverse indexing shown in white, we would have to account for that fact in the data transfer. The idea in the Cerberus coupling is to allow the coupled solvers to send and receive data in their preferred indexing, so that the coupled solvers do not have to rearrange data when sending or receiving it. This is achieved by the option to provide an indexing array as a part of a field template.

The indexing array, which needs to be sent if the indexing flag in the sent field template is set to 1 is simply an array of integers with the length of the array corresponding to the number of cells in the mesh and the contents of the array describing which solver index (white) corresponds to which global index (red). The first value of the array indicates the solver index corresponding to global index 1 and so on.

The indexing array for our 2x2 example above would thus be

4 3 2 1

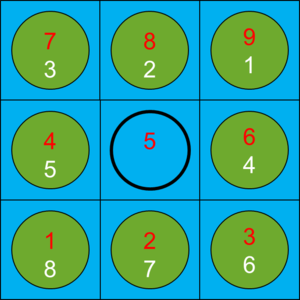
The indexing array can also account for the fact that the coupled solver will not accept or provide data for specific cell index/indices. If the coupled solver would only provide data for fuel rods and the geometry for the simulation would be as follows:

In this case the coupled solver does not consider the global cell 5 to be a part of its solution domain and thus will not provide or accept field data for that cell. Global cell 5 can be left un-indexed by setting the value 0 for it in the indexing array, which would now be

8 7 6 5 0 4 3 2 1

In such cases where some mesh cells are not indexed, the number of values for the field transferred between Cerberus and the solver will be reduced. In this case only 8 values would be transferred in the giveFieldData and takeFieldData calls.

Extending the previous example from 3x3x1 to 3x3x2 the indexing array might be

8 7 6 5 0 4 3 2 1 16 15 14 13 0 12 11 10 9

assuming that the indexing of the coupled solver on the upper axial layer is similar to that in the lower axial layer shown in the previous figure.