Variance reduction
Variance reduction in Serpent is based on standard weight-window techniques.[1] The weight window mesh and additional parameters are defined using the wwin card. Serpent supports two mesh types:
- Weight-window mesh generated using the built-in response matrix method-based solver (see the wgen card).
- MCNP WWINP format weight window-mesh.[2]
This tutorial demonstrates the basic functionality of the built-in solver. The methodology is described in the related publications.[3][4]
Contents
Shielding calculation example
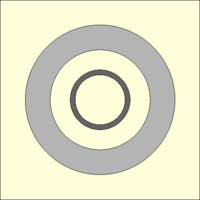
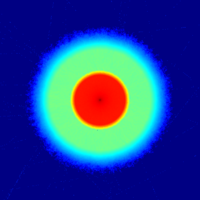
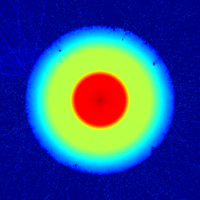
The test case is comprised of an isotropic, point-wise, low-energy neutron source, enclosed inside two cylindrical shells made of steel and concrete. The geometry is in 2D for the sake of simplicity, but the same procedures apply to 3D problems as well. The geometry plot and complete input listing are provided below (click Expand to show).
Completely made-up neutron shielding problem
% --- Geometry (nested cylinders) surf 1 cyl 0.0 0.0 100.0 surf 2 cyl 0.0 0.0 120.0 surf 3 cyl 0.0 0.0 200.0 surf 4 cyl 0.0 0.0 300.0 surf 5 sqc 0.0 0.0 400.0 cell 1 0 air -1 cell 2 0 steel 1 -2 cell 3 0 air 2 -3 cell 4 0 concrete 3 -4 cell 5 0 air 4 -5 cell 6 0 outside 5 % --- Materials mat steel -8.00000E+00 rgb 100 100 100 6000.03c -4.00000E-04 14000.03c -5.00000E-03 15031.03c -2.30000E-04 16000.03c -1.50000E-04 24000.03c -1.90000E-01 25055.03c -1.00000E-02 26000.03c -7.01730E-01 28000.03c -9.25000E-02 mat air -1.20500E-03 rgb 255 255 220 6000.03c -1.24000E-04 7014.03c -7.55268E-01 8016.03c -2.31781E-01 18040.03c -1.28270E-02 mat concrete -2.30000E+00 rgb 180 180 180 1001.03c -1.00000E-02 8016.03c -5.32000E-01 11023.03c -2.90000E-02 13027.03c -3.40000E-02 14000.03c -3.37000E-01 20000.03c -4.40000E-02 26000.03c -1.40000E-02 % --- Source src 1 sp 0 0 0 se 1E-6 % Isotropic 1 eV point source set srcrate 1 % Normalize to unit source rate % --- Run parameters set nps 200000 50 set gcu -1 % Group constant generation off % --- Geometry plot: plot 3 500 500 % --- Mesh plot (flux) det F1 % Flux detector mesh 8 -4 F1 3 500 500 % Plot detector scores % --- Detectors det d1 dc 3 % Flux in airspace between walls surf s2 cyl 0.0 160.0 5.0 det d2 dtl s2 % Flux at y = 160 (between the walls) surf s3 cyl 0.0 350.0 5.0 det d3 dtl s3 % Flux at y = 350 (outside the concrete wall)
Notes on the input:
- Group constant generation is on by default in neutron transport simulations. This is switched off by set gcu -1.
- Neutron transport simulations are normalized by default to unit loss rate. For consistency the normalization is changed to unit source rate by set srcrate 1.
- The mesh-card is linked to a flux detector (type 8) to visualize the effect of variance reduction. The color scheme is set to logarithmic (negative entry). It should be noted that the normalization of the color scheme depends on the minimum and maximum values, so the plots produced with and without variance reduction are not similarly normalized.
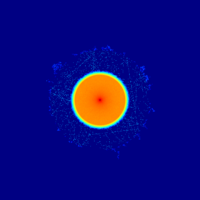
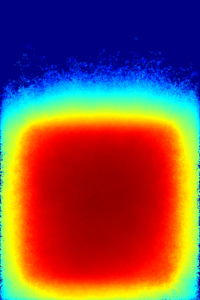
In addition to the mesh plot, flux is also calculated using a cell flux detector in the airspace between the walls (d1) and two track-length detectors at a position between the walls (d2) and outside the outer concrete wall (d3). The mesh plot and detector results are presented below (click image for full-size).
| Detector | Score | Relative statistical error |
|---|---|---|
| d1 (volume flux between shells) | 1.59600E-01 | 0.16735 |
| d2 (at y = 160) | 1.04553E-04 | 0.73813 |
| d3 (at y = 350) | 0.00000E+00 | 0.00000 |
The results show that most neutrons are stopped by the inner shell, and none of the particles are able to penetrate the concrete.
Variance reduction, simple approach
The simplest approach to applying variance reduction is to divide the calculation in two parts. The first run generates the importance mesh, and the second run produces the final results by applying the weight-window technique. The weigh window generator is invoked by adding the wgen card:
Complete input
% --- Geometry (nested cylinders) surf 1 cyl 0.0 0.0 100.0 surf 2 cyl 0.0 0.0 120.0 surf 3 cyl 0.0 0.0 200.0 surf 4 cyl 0.0 0.0 300.0 surf 5 sqc 0.0 0.0 400.0 cell 1 0 air -1 cell 2 0 steel 1 -2 cell 3 0 air 2 -3 cell 4 0 concrete 3 -4 cell 5 0 air 4 -5 cell 6 0 outside 5 % --- Materials mat steel -8.00000E+00 rgb 100 100 100 6000.03c -4.00000E-04 14000.03c -5.00000E-03 15031.03c -2.30000E-04 16000.03c -1.50000E-04 24000.03c -1.90000E-01 25055.03c -1.00000E-02 26000.03c -7.01730E-01 28000.03c -9.25000E-02 mat air -1.20500E-03 rgb 255 255 220 6000.03c -1.24000E-04 7014.03c -7.55268E-01 8016.03c -2.31781E-01 18040.03c -1.28270E-02 mat concrete -2.30000E+00 rgb 180 180 180 1001.03c -1.00000E-02 8016.03c -5.32000E-01 11023.03c -2.90000E-02 13027.03c -3.40000E-02 14000.03c -3.37000E-01 20000.03c -4.40000E-02 26000.03c -1.40000E-02 % --- Source src 1 sp 0 0 0 se 1E-6 % Isotropic 1 eV point source set srcrate 1 % Normalize to unit source rate % --- Run parameters set nps 200000 50 set gcu -1 % Group constant generation off % --- Geometry plot: plot 3 500 500 % --- Mesh plot (flux) det F1 % Flux detector mesh 8 -4 F1 3 500 500 % Plot detector scores % --- Detectors det d1 dc 3 % Flux in airspace between walls surf s2 cyl 0.0 160.0 5.0 det d2 dtl s2 % Flux at y = 160 (between the walls) surf s3 cyl 0.0 350.0 5.0 det d3 dtl s3 % Flux at y = 350 (outside the concrete wall) % --- Weight window generation wwgen 1 % wwgen identifier 1E-9 10000 % convergence criteria 1 -1 % single detector, no energy binning 1 % Cartesian mesh -400.01 400.01 51 % x-dimensions -400.01 400.01 51 % y-dimensions -1E18 1E18 1 % z-dimensions d2 1.0 % detecor name and weight factor
Notes:
- The geometry is covered by a Cartesian 51x51x1 mesh.
- An uneven number of cells is selected to prevent the point source (at origin) coinciding with the mesh boundaries.
- The mesh should be slightly larger (here 0.01 cm) than the geometry to prevent problems with numerical precision.
- In 2D calculations the axial limits should be set to large values to prevent particles escaping the mesh.
- The importances are calculated with respect to detector d2, positioned between the two shells.
When Serpent is run, the run-time output shows some information on the response matrix solution:
If the solution does not converge, the reason is most likely poor statistics.
The calculation produces a binary weight-window mesh file: [input].wwd, which can be read into another simulation using the wwin card:
Complete input
% --- Geometry (nested cylinders) surf 1 cyl 0.0 0.0 100.0 surf 2 cyl 0.0 0.0 120.0 surf 3 cyl 0.0 0.0 200.0 surf 4 cyl 0.0 0.0 300.0 surf 5 sqc 0.0 0.0 400.0 cell 1 0 air -1 cell 2 0 steel 1 -2 cell 3 0 air 2 -3 cell 4 0 concrete 3 -4 cell 5 0 air 4 -5 cell 6 0 outside 5 % --- Materials mat steel -8.00000E+00 rgb 100 100 100 6000.03c -4.00000E-04 14000.03c -5.00000E-03 15031.03c -2.30000E-04 16000.03c -1.50000E-04 24000.03c -1.90000E-01 25055.03c -1.00000E-02 26000.03c -7.01730E-01 28000.03c -9.25000E-02 mat air -1.20500E-03 rgb 255 255 220 6000.03c -1.24000E-04 7014.03c -7.55268E-01 8016.03c -2.31781E-01 18040.03c -1.28270E-02 mat concrete -2.30000E+00 rgb 180 180 180 1001.03c -1.00000E-02 8016.03c -5.32000E-01 11023.03c -2.90000E-02 13027.03c -3.40000E-02 14000.03c -3.37000E-01 20000.03c -4.40000E-02 26000.03c -1.40000E-02 % --- Source src 1 sp 0 0 0 se 1E-6 % Isotropic 1 eV point source set srcrate 1 % Normalize to unit source rate % --- Run parameters set nps 200000 50 set gcu -1 % Group constant generation off set bala 1 % Use OMP load balancing % --- Geometry plot: plot 35 1E-4 1E4 -1 500 500 % --- Mesh plot (flux) det F1 % Flux detector mesh 8 -4 F1 3 500 500 % Plot detector scores % --- Detectors det d1 dc 3 % Flux in airspace between walls surf s2 cyl 0.0 160.0 5.0 det d2 dtl s2 % Flux at y = 160 (between the walls) surf s3 cyl 0.0 350.0 5.0 det d3 dtl s3 % Flux at y = 350 (outside the concrete wall) % --- Weight windows wwin 1 wf "YOUR_FILE.wwd" 1 % Read from previous run
Notes on the input:
- Variance reduction causes splitting of the particle histories, which may result in deterioration of OpenMP parallel scalability. To improve performance, it is recommended to switch OpenMP load balancing on by set bala 1.
- The importance mesh can be plotted on top of the geometry using the plot card. The additional input parameters include importance boundaries and energy (for energy-dependent calculations).
- The current version of Serpent (2.2.0) does not plot the mesh grid for the importance distribution, but this can be enabled by removing the "wwp = NO;" statement on line 42 of plotimage.c
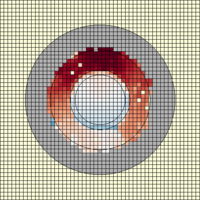
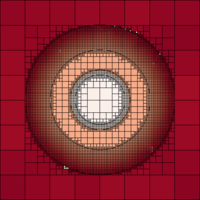
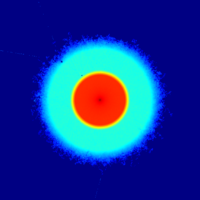
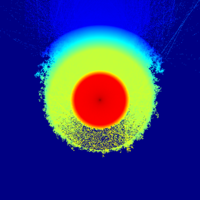
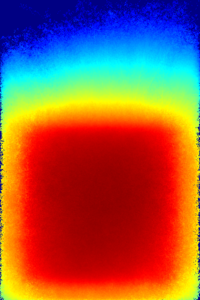
The mesh plot and detector results using variance reduction are presented below (click image for full-size).
| Detector | Score | Relative statistical error |
|---|---|---|
| d1 (volume flux between shells) | 1.18215E-01 | 0.14545 |
| d2 (at y = 160) | 1.50203E-04 | 0.10000 |
| d3 (at y = 350) | 0.00000E+00 | 0.00000 |
The importances were calculated with respect to detector d2, which recieves much better statistics compared to the analog calculation. The mesh plot shows how the calculated flux is concentrated around the detectors, as particles less likely to contribute to the result are killed by Russian roulette. It should be noted that the result for d1 is no longer valid, since some of the contributing particles are killed.
Global variance reduction, fixed mesh
One of the challenges with large and heavily shielded geometries is that the particle histories may not reach the region of interest, in which case the Monte Carlo simulation fails to provide the coupling coefficients for the response matrix method-based importance solver. The solution is to apply global variance reduction (GVR), which means producing a weight-window mesh that uniformly populates the entire geometry. The calculation proceeds by iterations. Each cycle allows the particles to wonder beyond the region charted for the weight-window mesh, and the collected new data is used to extend the mesh deeper into the geometry.
This option is invoked by setting the MOD parameter to 3 in the wgen card. Also the detector entry is left out. The mesh type is changed to cylindrical. In this example global variance reduction is used with weight window iterations. The input is listed below.
Complete input
% --- Geometry (nested cylinders) surf 1 cyl 0.0 0.0 100.0 surf 2 cyl 0.0 0.0 120.0 surf 3 cyl 0.0 0.0 200.0 surf 4 cyl 0.0 0.0 300.0 surf 5 sqc 0.0 0.0 400.0 cell 1 0 air -1 cell 2 0 steel 1 -2 cell 3 0 air 2 -3 cell 4 0 concrete 3 -4 cell 5 0 air 4 -5 cell 6 0 outside 5 % --- Materials mat steel -8.00000E+00 rgb 100 100 100 6000.03c -4.00000E-04 14000.03c -5.00000E-03 15031.03c -2.30000E-04 16000.03c -1.50000E-04 24000.03c -1.90000E-01 25055.03c -1.00000E-02 26000.03c -7.01730E-01 28000.03c -9.25000E-02 mat air -1.20500E-03 rgb 255 255 220 6000.03c -1.24000E-04 7014.03c -7.55268E-01 8016.03c -2.31781E-01 18040.03c -1.28270E-02 mat concrete -2.30000E+00 rgb 180 180 180 1001.03c -1.00000E-02 8016.03c -5.32000E-01 11023.03c -2.90000E-02 13027.03c -3.40000E-02 14000.03c -3.37000E-01 20000.03c -4.40000E-02 26000.03c -1.40000E-02 % --- Source src 1 sp 0 0 0 se 1E-6 % Isotropic 1 eV point source set srcrate 1 % Normalize to unit source rate % --- Run parameters set nps 200000 50 set gcu -1 % Group constant generation off set bala 1 % Use OMP load balancing % --- Geometry plot: plot 35 1E-9 1E9 -1 500 500 % --- Mesh plot (flux) det F1 % Flux detector mesh 8 -4 F1 3 500 500 % Plot detector scores % --- Detectors det d1 dc 3 % Flux in airspace between walls surf s2 cyl 0.0 160.0 5.0 det d2 dtl s2 % Flux at y = 160 (between the walls) surf s3 cyl 0.0 350.0 5.0 det d3 dtl s3 % Flux at y = 350 (outside the concrete wall) % --- Weight window generation wwgen 1 % wwgen identifier 1E-9 10000 % convergence criteria 3 -1 % global variance reduction, no energy binning 2 % cylindrical mesh 0.0 565.70 50 % radial dimensions 0.0 360.00 1 % azimuthal dimensions -1E18 1E18 1 % axial dimensions % --- GVR iterations wwin 1 wi 1 3 % 3 iterations using the same mesh 1 1.0 1 1.0 1 1.0
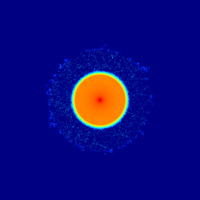
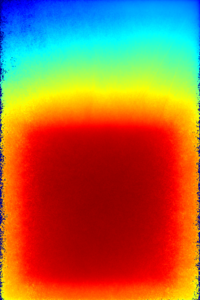
The geometry and mesh plots and detector results are presented below.
| Detector | Score | Relative statistical error |
|---|---|---|
| d1 (volume flux between shells) | 1.67545E-01 | 0.02275 |
| d2 (at y = 160) | 1.48163E-04 | 0.05940 |
| d3 (at y = 350) | 4.51737E-10 | 0.09170 |
The GVR iterations push particle population through the shielded parts of the geometry, resulting in non-zero statistics olso for the outermost detector.
Global variance reduction, adaptive mesh
The most elaborate solution to deep penetration problems is to first run GVR iterations until the region of interest is populated, and then produce the optimal weight-window mesh for the detector. In practice this involves three runs:
- GVR iteration until the geometry is sufficiently populated
- Generation of the optimal weight-window mesh
- Final transport simulation using the optimal mesh.
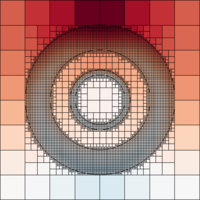
This approach is demonstrated using the adaptive mesh option. A coarse Cartesian base mesh is laid on top of the geometry, and the cells are recursively split to adapt the mesh around the dense parts of the geometry. The input is listed below.
Complete input
% --- Geometry (nested cylinders) surf 1 cyl 0.0 0.0 100.0 surf 2 cyl 0.0 0.0 120.0 surf 3 cyl 0.0 0.0 200.0 surf 4 cyl 0.0 0.0 300.0 surf 5 sqc 0.0 0.0 400.0 cell 1 0 air -1 cell 2 0 steel 1 -2 cell 3 0 air 2 -3 cell 4 0 concrete 3 -4 cell 5 0 air 4 -5 cell 6 0 outside 5 % --- Materials mat steel -8.00000E+00 rgb 100 100 100 6000.03c -4.00000E-04 14000.03c -5.00000E-03 15031.03c -2.30000E-04 16000.03c -1.50000E-04 24000.03c -1.90000E-01 25055.03c -1.00000E-02 26000.03c -7.01730E-01 28000.03c -9.25000E-02 mat air -1.20500E-03 rgb 255 255 220 6000.03c -1.24000E-04 7014.03c -7.55268E-01 8016.03c -2.31781E-01 18040.03c -1.28270E-02 mat concrete -2.30000E+00 rgb 180 180 180 1001.03c -1.00000E-02 8016.03c -5.32000E-01 11023.03c -2.90000E-02 13027.03c -3.40000E-02 14000.03c -3.37000E-01 20000.03c -4.40000E-02 26000.03c -1.40000E-02 % --- Source src 1 sp 0 0 0 se 1E-6 % Isotropic 1 eV point source set srcrate 1 % Normalize to unit source rate % --- Run parameters set nps 200000 50 set gcu -1 % Group constant generation off set bala 1 % Use OMP load balancing % --- Geometry plot: plot 35 1E-9 1E9 -1 500 500 % --- Mesh plot (flux) det F1 % Flux detector mesh 8 -4 F1 3 500 500 % Plot detector scores % --- Detectors det d1 dc 3 % Flux in airspace between walls surf s2 cyl 0.0 160.0 5.0 det d2 dtl s2 % Flux at y = 160 (between the walls) surf s3 cyl 0.0 350.0 5.0 det d3 dtl s3 % Flux at y = 350 (outside the concrete wall) % --- Weight window generation wwgen 1 % wwgen identifier 1E-9 10000 % convergence criteria 3 -1 % global variance reduction, no energy binning 1 % cartesian mesh -400.01 400.01 2 % x-dimensions -400.01 400.01 2 % y-dimensions -1E18 1E18 1 % z-dimensions % --- Generation of Adaptive mesh and iterations wwin 1 wi 2 4 1 % run 4 iterations with adaptive mesh 2 2 1 % split cells in half (x and y only) 10 2000 % 10 outer iterations 2000 tracks 1E9 1000000 % importance and neighbor criteria -1.0 5.0 5.0 5.0 % density criteria and minimum dimensions
Notes on the input:
- The adaptive mesh is generated based on split and stop criteria.
- When split, the cells are divided into 2x2x1 new cells (2D geometry, no splitting in z).
- In this example the splits are based on the density criterion only. The importance and neighbor criteria are eliminated by using high limits.
- Splitting occurs if the cell contains a dense material (density above 1.0 g/cm3), unless the size is already below the minimum (5x5x5 cm).
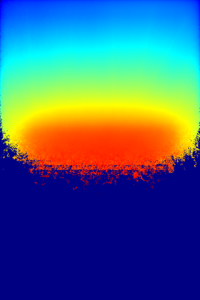
The geometry and mesh plots and detector results are presented below.
| Detector | Score | Relative statistical error |
|---|---|---|
| d1 (volume flux between shells) | 1.64883E-01 | 0.01643 |
| d2 (at y = 160) | 1.55702E-04 | 0.02679 |
| d3 (at y = 350) | 4.30948E-10 | 0.05926 |
The GVR iterations produce 4 weight window files [input].wwd0 ... [input].wwd3. The last mesh is next used for variance reduction in the next simulation, in which the weight-window mesh is optimized for detector d3:
Complete input
% --- Geometry (nested cylinders) surf 1 cyl 0.0 0.0 100.0 surf 2 cyl 0.0 0.0 120.0 surf 3 cyl 0.0 0.0 200.0 surf 4 cyl 0.0 0.0 300.0 surf 5 sqc 0.0 0.0 400.0 cell 1 0 air -1 cell 2 0 steel 1 -2 cell 3 0 air 2 -3 cell 4 0 concrete 3 -4 cell 5 0 air 4 -5 cell 6 0 outside 5 % --- Materials mat steel -8.00000E+00 rgb 100 100 100 6000.03c -4.00000E-04 14000.03c -5.00000E-03 15031.03c -2.30000E-04 16000.03c -1.50000E-04 24000.03c -1.90000E-01 25055.03c -1.00000E-02 26000.03c -7.01730E-01 28000.03c -9.25000E-02 mat air -1.20500E-03 rgb 255 255 220 6000.03c -1.24000E-04 7014.03c -7.55268E-01 8016.03c -2.31781E-01 18040.03c -1.28270E-02 mat concrete -2.30000E+00 rgb 180 180 180 1001.03c -1.00000E-02 8016.03c -5.32000E-01 11023.03c -2.90000E-02 13027.03c -3.40000E-02 14000.03c -3.37000E-01 20000.03c -4.40000E-02 26000.03c -1.40000E-02 % --- Source src 1 sp 0 0 0 se 1E-6 % Isotropic 1 eV point source set srcrate 1 % Normalize to unit source rate % --- Run parameters set nps 200000 50 set gcu -1 % Group constant generation off set bala 1 % Use OMP load balancing % --- Geometry plot: plot 35 1E-9 1E9 -1 500 500 % --- Mesh plot (flux) det F1 % Flux detector mesh 8 -4 F1 3 500 500 % Plot detector scores % --- Detectors det d1 dc 3 % Flux in airspace between walls surf s2 cyl 0.0 160.0 5.0 det d2 dtl s2 % Flux at y = 160 (between the walls) surf s3 cyl 0.0 350.0 5.0 det d3 dtl s3 % Flux at y = 350 (outside the concrete wall) % --- Weight window generation wwgen 1 % wwgen identifier 1E-9 10000 % convergence criteria 1 -1 % single detector, no energy binning -1 % use mesh from file d3 1.0 % --- Weight windows wwin 1 wf "YOUR_FILE1.wwd3" 1 % read last mesh from previous iteration
Notes:
- The mesh type in the wgen card must be set to -1 when the mesh is read from a file.
- The type is again set to 1 (single detector) and the detector entry added at the end.
The result is a final weight-window mesh file, optimized for detector d3. This mesh is read into the third input:
Complete input
% --- Geometry (nested cylinders) surf 1 cyl 0.0 0.0 100.0 surf 2 cyl 0.0 0.0 120.0 surf 3 cyl 0.0 0.0 200.0 surf 4 cyl 0.0 0.0 300.0 surf 5 sqc 0.0 0.0 400.0 cell 1 0 air -1 cell 2 0 steel 1 -2 cell 3 0 air 2 -3 cell 4 0 concrete 3 -4 cell 5 0 air 4 -5 cell 6 0 outside 5 % --- Materials mat steel -8.00000E+00 rgb 100 100 100 6000.03c -4.00000E-04 14000.03c -5.00000E-03 15031.03c -2.30000E-04 16000.03c -1.50000E-04 24000.03c -1.90000E-01 25055.03c -1.00000E-02 26000.03c -7.01730E-01 28000.03c -9.25000E-02 mat air -1.20500E-03 rgb 255 255 220 6000.03c -1.24000E-04 7014.03c -7.55268E-01 8016.03c -2.31781E-01 18040.03c -1.28270E-02 mat concrete -2.30000E+00 rgb 180 180 180 1001.03c -1.00000E-02 8016.03c -5.32000E-01 11023.03c -2.90000E-02 13027.03c -3.40000E-02 14000.03c -3.37000E-01 20000.03c -4.40000E-02 26000.03c -1.40000E-02 % --- Source src 1 sp 0 0 0 se 1E-6 % Isotropic 1 eV point source set srcrate 1 % Normalize to unit source rate % --- Run parameters set nps 200000 50 set gcu -1 % Group constant generation off set bala 1 % Use OMP load balancing % --- Geometry plot: plot 35 1E-9 1E9 -1 500 500 % --- Mesh plot (flux) det F1 % Flux detector mesh 8 -4 F1 3 500 500 % Plot detector scores % --- Detectors det d1 dc 3 % Flux in airspace between walls surf s2 cyl 0.0 160.0 5.0 det d2 dtl s2 % Flux at y = 160 (between the walls) surf s3 cyl 0.0 350.0 5.0 det d3 dtl s3 % Flux at y = 350 (outside the concrete wall) % --- Weight windows wwin 1 wf "YOUR_FILE2.wwd" 1
The geometry and mesh plots and detector results are presented below.
| Detector | Score | Relative statistical error |
|---|---|---|
| d1 (volume flux between shells) | 1.73844E-01 | 0.08012 |
| d2 (at y = 160) | 1.61522E-04 | 0.02736 |
| d3 (at y = 350) | 4.64133E-10 | 0.03110 |
The statistics for detector d3 are again improved. It should be noted that the result for d1 is no longer valid, since some of the contributing particles are killed by Russian roulette.
Reactor calculation example
Typical applications for variance reduction in fission reactor calculations include obtaining better statistics for detectors or radiation dose rates outside the active core. Since the methodology is currently not applicable to criticality source simulations, the calculation has to be divided in two parts:
- Criticality source simulation to obtain the fission source using the set csw option.
- External source simulation using the previously created fission source (sf parameter in the source card) and fission reactions switched off (set nphys option).
Variance reduction is performed on the second part.
The example case is a homogenized LWR reactor core (never apply this approximation in a real calculation) surrounded by water reflector and cylindrical pressure vessel. The task is to calculate neutron current through the top of the geometry, which is the most heavily shielded part. The geometry and fission rate / thermal flux mesh plots and the complete input listing are provided below (click Expand to show).
Completely made-up reactor problem
% --- UO2 fuel enriched to 3.6 wt-% U-235: mat fuel -10.45700 92235.09c -0.03173 92238.09c -0.84977 8016.09c -0.11850 % --- Zr-Nb cladding and shroud tube: mat clad -6.55000 40000.06c -0.99000 41093.06c -0.01000 % --- Water with boron: mat water -0.7207 moder lwtr 1001 rgb 64 164 223 1001.06c 2.0 8016.06c 1.0 5010.06c 940E-6 therm lwtr lwj3.11t mat steel -8.00000E+00 rgb 100 100 100 6000.03c -4.00000E-04 14000.03c -5.00000E-03 15031.03c -2.30000E-04 16000.03c -1.50000E-04 24000.03c -1.90000E-01 25055.03c -1.00000E-02 26000.03c -7.01730E-01 28000.03c -9.25000E-02 % --- Homogenized core (bad approximation, used for demo purposes only): mix core rgb 255 191 0 fuel -0.674533 clad -0.242370 water -0.083096 % --- Geometry surf 1 cyl 0.0 0.0 150.0 0.0 300.0 surf 2 cyl 0.0 0.0 170.0 -20.0 540.0 surf 3 cyl 0.0 0.0 200.0 -40.0 560.0 cell 1 0 core -1 cell 2 0 water 1 -2 cell 3 0 steel 2 -3 cell 4 0 outside 3 % --- Run parameters: set pop 10000 100 100 set gcu -1 % --- Write source in file: set csw "fiss.src" % --- Geometry plot and mesh plots: plot 1 400 600 mesh 1 400 600
Variance reduction is performed in the external source mode with fissions switched off using the source distribution from the analog criticality source simulation. The calculation is performed in the iterative mode, using an unevenly-spaced cylindrical weight-window mesh. Three GVR iterations are first run to obtain statistics for the surface current detector placed at the top of the geometry (detector d1). This is then followed by mesh generation optimized for the detector, and the final calculation. Two wwgen-cards are defined. The mesh is the same in both cases, the only difference is how the importances are calculated. The input is listed below.
Complete input
% --- UO2 fuel enriched to 3.6 wt-% U-235:
mat fuel -10.45700
92235.09c -0.03173
92238.09c -0.84977
8016.09c -0.11850
% --- Zr-Nb cladding and shroud tube:
mat clad -6.55000
40000.06c -0.99000
41093.06c -0.01000
% --- Water with boron:
mat water -0.7207 moder lwtr 1001 rgb 64 164 223
1001.06c 2.0
8016.06c 1.0
5010.06c 940E-6
therm lwtr lwj3.11t
mat steel -8.00000E+00 rgb 100 100 100
6000.03c -4.00000E-04
14000.03c -5.00000E-03
15031.03c -2.30000E-04
16000.03c -1.50000E-04
24000.03c -1.90000E-01
25055.03c -1.00000E-02
26000.03c -7.01730E-01
28000.03c -9.25000E-02
% --- Homogenized core (bad approximation, used for demo purposes only):
mix core rgb 255 191 0
fuel -0.674533
clad -0.242370
water -0.083096
% --- Geometry
surf 1 cyl 0.0 0.0 150.0 0.0 300.0
surf 2 cyl 0.0 0.0 170.0 -20.0 540.0
surf 3 cyl 0.0 0.0 200.0 -40.0 560.0
cell 1 0 core -1
cell 2 0 water 1 -2
cell 3 0 steel 2 -3
cell 4 0 outside 3
% --- Run parameters:
set nps 1000000 100
set srcrate 1
set gcu -1
set bala 1
set nbuf 10000
% --- Geometry plot with importances:
plot 15 1E-12 1E12 1.0 400 600
% --- Mesh plot (flux)
det F1 % Flux detector
mesh 8 -4 F1 1 400 600 % Plot detector scores
% --- Source:
src 1 sf "fiss.src" 1
% --- Fissions off:
set nphys 0
% --- First weight window mesh (GVR):
wwgen 1 % wwgen identifier
1E-9 10000 % convergence criteria
3 -1 % global variance reduction, no energy binning
8 % unevenly spaced cylindrical mesh
3 1 86 % size in r, theat and z dimensions
0 150 170 200.01 % 3 r-bins
0 360 % single theta-bin
-40.01 % 86 z-bins
-30 -20 -10 0 % 10 cm intervals until top of core
10 20 30 40
50 60 70 80
90 100 110 120
130 140 150 160
170 180 190 200
210 220 230 240
250 260 270 280
290 300 305 310 % 5 cm intervals from here on
315 320 325 330
335 340 345 350
355 360 365 370
375 380 385 390
395 400 405 410
415 420 425 430
435 440 445 450
455 460 465 470
475 480 485 490
495 500 505 510
515 520 525 530
535 540 545 550
555 560.01
% --- Detector (surface current through top plane)
surf d1 pz 560
det d1 ds d1 1
% --- Second weight window mesh (detector):
wwgen 2 % wwgen identifier
1E-9 10000 % convergence criteria
1 -1 % single detector, no energy binning
8 % unevenly spaced cylindrical mesh
3 1 86 % size in r, theat and z dimensions
0 150 170 200.01 % 3 r-bins
0 360 % single theta-bin
-40.01 % 86 z-bins
-30 -20 -10 0 % 10 cm intervals until top of core
10 20 30 40
50 60 70 80
90 100 110 120
130 140 150 160
170 180 190 200
210 220 230 240
250 260 270 280
290 300 305 310 % 5 cm intervals from here on
315 320 325 330
335 340 345 350
355 360 365 370
375 380 385 390
395 400 405 410
415 420 425 430
435 440 445 450
455 460 465 470
475 480 485 490
495 500 505 510
515 520 525 530
535 540 545 550
555 560.01
d1 1.0
% --- Weight window iterations:
wwin 1
wi 1 5 % 3 + 2 iterations (last for final results)
1 1.0
1 1.0
1 1.0
2 1.0
2 1.0
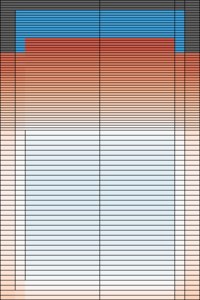
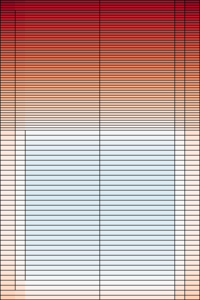
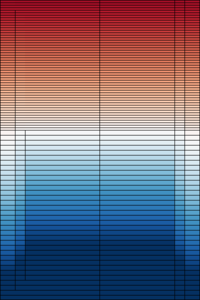
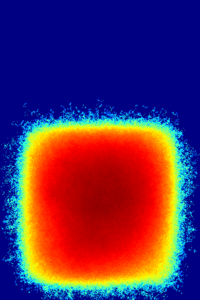
The importance mesh and flux distributions throughout the iteration are plotted below.
The outward current is around 6E-13. Since the source rate was normalized to unity, this means that fewer than 1/1E12 fission neutrons are able to escape through the top. It should be noted that the calculation was run with a relatively small number of neutron histories, and the mesh generation suffers from poor statistics.
References
- ^ Lux, I. and Koblinger, L. "Monte Carlo Particle Transport Methods: Neutron and Photon Calculations." CRC-Press, Inc (1991).
- ^ Kulesza, J. A. (ed.), “MCNP code version 6.3.0 Theory & User Manual: Appendix A Mesh-Based WWINP, WWOUT, and WWONE File Format,” LA-UR-22-30006, Rev. 1, Los Alamos National Laboratory (2022).
- ^ Leppänen, J. "Response Matrix Method–Based Importance Solver and Variance Reduction Scheme in the Serpent 2 Monte Carlo Code." Nucl. Technol. 205 (11) (2019) 1416-1432
- ^ Leppänen, J. and Jokipii, M. "Global Variance Reduction Scheme with Self-Adaptive Weight-Window Mesh in the Serpent 2 Monte Carlo Code." In Proc. M&C2019, Portland, OR, Aug. 25-29, 2019.