Difference between revisions of "Variance reduction"
(→Test case and analog simulation) |
(→Variance reduction, simple approach) |
||
| Line 118: | Line 118: | ||
== Variance reduction, simple approach == | == Variance reduction, simple approach == | ||
| + | |||
| + | The simplest approach to applying variance reduction is to divide the calculation in two parts. The first run generates the importance mesh, and the second run produces the final results by applying the weight-window technique. | ||
== References == | == References == | ||
Revision as of 15:56, 4 October 2019
Variance reduction in Serpent is based on standard weight-window techniques.[1] The weight window mesh and additional parameters are defined using the wwin card. Serpent supports two mesh types:
- Weight-window mesh generated using the built-in response matrix method-based solver (see the wgen card).
- MCNP WWINP format weight window-mesh.[2]
This tutorial demonstrates the basic functionality of the built-in solver. The methodology is described in the related publications.[3][4]
Test case and analog simulation
The test case is comprised of an isotropic, point-wise, low-energy neutron source, enclosed inside two cylindrical shells made of steel and concrete. The geometry is in 2D for the sake of simplicity, but the same procedures apply to 3D problems as well. The geometry plot and complete input listing are provided below (click Expand to show).
Completely made-up neutron shielding problem
% --- Geometry (nested cylinders) surf 1 cyl 0.0 0.0 100.0 surf 2 cyl 0.0 0.0 120.0 surf 3 cyl 0.0 0.0 200.0 surf 4 cyl 0.0 0.0 300.0 surf 5 sqc 0.0 0.0 400.0 cell 1 0 air -1 cell 2 0 steel 1 -2 cell 3 0 air 2 -3 cell 4 0 concrete 3 -4 cell 5 0 air 4 -5 cell 6 0 outside 5 % --- Materials mat steel -8.00000E+00 rgb 100 100 100 6000.03c -4.00000E-04 14000.03c -5.00000E-03 15031.03c -2.30000E-04 16000.03c -1.50000E-04 24000.03c -1.90000E-01 25055.03c -1.00000E-02 26000.03c -7.01730E-01 28000.03c -9.25000E-02 mat air -1.20500E-03 rgb 255 255 220 6000.03c -1.24000E-04 7014.03c -7.55268E-01 8016.03c -2.31781E-01 18040.03c -1.28270E-02 mat concrete -2.30000E+00 rgb 180 180 180 1001.03c -1.00000E-02 8016.03c -5.32000E-01 11023.03c -2.90000E-02 13027.03c -3.40000E-02 14000.03c -3.37000E-01 20000.03c -4.40000E-02 26000.03c -1.40000E-02 % --- Source src 1 sp 0 0 0 se 1E-6 % Isotropic 1 eV point source set srcrate 1 % Normalize to unit source rate % --- Run parameters set nps 200000 50 set gcu -1 % Group constant generation off % --- Geometry plot: plot 3 500 500 % --- Mesh plot (flux) det F1 % Flux detector mesh 8 -4 F1 3 500 500 % Plot detector scores % --- Detectors det d1 dc 3 % Flux in airspace between walls surf s2 cyl 0.0 160.0 5.0 det d2 dtl s2 % Flux at y = 160 (between the walls) surf s3 cyl 0.0 350.0 5.0 det d3 dtl s3 % Flux at y = 350 (outside the concrete wall)
Notes on the input:
- Group constant generation is on by default in neutron transport simulations. This is switched off by set gcu -1.
- Neutron transport simulations are normalized by default to unit loss rate. For consistency the normalization is changed to unit source rate by set srcrate 1.
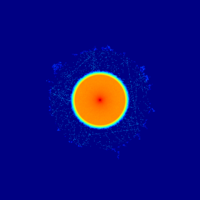
- The mesh-card is linked to a flux detector (type 8) to visualize the effect of variance reduction. The color scheme is set to logarithmic (negative entry). It should be noted that the normalization of the color scheme depends on the minimum and maximum values, so the plots produced with and without variance reduction are not similarly normalized.
In addition to the mesh plot, flux is also calculated using a cell flux detector in the airspace between the walls (d1) and two track-length detectors at a position between the walls (d2) and outside the outer concrete wall (d3). The mesh plot and detector results are presented below (click image for full-size).
| Detector | Score | Relative statistical error |
|---|---|---|
| d1 (volume flux between shells) | 1.59600E-01 | 0.16735 |
| d2 (at y = 160) | 1.04553E-04 | 0.73813 |
| d3 (at y = 350) | 0.00000E+00 | 0.00000 |
The results show that most neutrons are stopped by the inner shell, and none of the particles are able to penetrate the concrete.
Variance reduction, simple approach
The simplest approach to applying variance reduction is to divide the calculation in two parts. The first run generates the importance mesh, and the second run produces the final results by applying the weight-window technique.
References
- ^ Lux, I. and Koblinger, L. "Monte Carlo Particle Transport Methods: Neutron and Photon Calculations." CRC-Press, 1991. (available on-line).
- ^ D. Pelowitz (ed.), “MCNP6 User’s Manual: Appendix C Mesh-Based WWINP, WWOUT, and WWONE File Format,” LA-CP-13-00634, Los Alamos National Laboratory (2013).
- ^ J. Leppänen "Response Matrix Method–Based Importance Solver and Variance Reduction Scheme in the Serpent 2 Monte Carlo Code." Nucl. Technol. (in press)
- ^ J. Leppänen and M. Jokipii. "Global Variance Reduction Scheme with Self-Adaptive Weight-Window Mesh in the Serpent 2 Monte Carlo Code." In Proc. M&C2019, Portland, OR, Aug. 25-29, 2019.