Universe symmetries
The fact that Serpent handles repeated boundary conditions by coordinate transformations rather than actual reflections and rotations limits their applicability to the creation of infinite lattices. In order to account for symmetries in geometries Serpent offers instead the universe symmetry option.
The method works by taking an angular segment of a universe, and repeating that over 360 degrees. The repetition can be done by either reflection (each repeated segment is a mirror image of its neighbours) or by periodic rotation. Anything that is originally modeled in the universe beyond the segment is covered by its copies.
The use of the symmetry option is demonstrated by examples below.
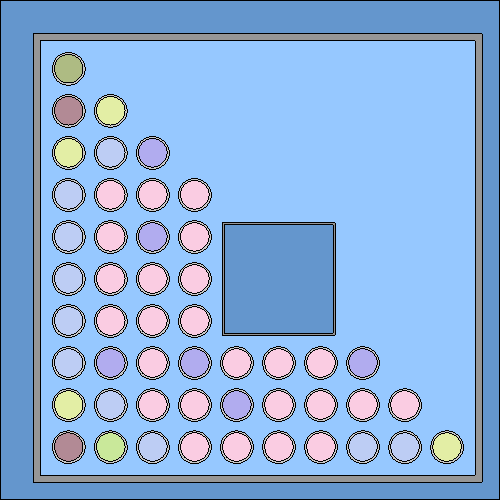
Consider a universe (10) consisting of a 10 by 10 assembly of fuel pins with the following pattern:
This universe can be manipulated using the symmetry card, for example by taking a 90 degree segment and filling the rest of the universe with its reflected copies:
set usym 10 3 2 0.0 0.0 0 90
The assebly is now filled with the yellow pins that make up the lower right quarter of the assembly:
Notice from the instrumentation tube positions how the segment is reflected over the boundary surfaces. If the angle is extended from 90 to 180 degrees:
set usym 10 3 2 0.0 0.0 0 180
the result is that the entire lower half is reflected:
In addition to the width of the segment, also the starting angle can be changed. Here is a 180 degree symmetry, tilted by 45 degrees:
set usym 10 3 2 0.0 0.0 45 180
The symmetry line now extends from the upper left to the lower right corner. A 90 degree symmetry, tilted by 45 degrees looks like this:
set usym 10 3 2 0.0 0.0 45 90
Each of the above examples show reflectional symmetry. This is what the previous figure would look like with periodic symmetry:
set usym 10 3 3 0.0 0.0 45 90
The method can really be abused for producing psychedelic patterns like:
set usym 10 3 3 0.0 0.0 15 15
One thing that is to be noted, though, is that if the symmetry is applied on the lowest universe, the shape of the outer boundary must be preserved in order to apply periodic or reflective boundary conditions. If this is not the case, the code will issue an error message on incompatible boundary conditions.
Of course the main reason for developing this methodology is not create interesting shapes, but to simplify the definition of geometries that have some level of symmetry. Consider, for example, a BWR fuel assembly with a 1/2 symmetry. The loading pattern can be defined in the input as:
If we wish to run a burnup calculation on this model, we can further divide the materials into separate depletion zones using the div card:
If we now apply the universe symmetry option (180 deg, tilted by 45 deg), we end up with a geometry that looks like:
In addition to the simplified input definition, the number of depletion zones is now reduced to minimum. If we had a full assembly model with the divisor cards, each pin would be handled as a separate depletion zone, without accounting for the symmetry. This can make a huge difference in the number of burnable materials and memory consumption in full core geometries.
It is important to note that one problem with this methodology is that the material volumes that Serpent calculates automatically correspond to the 1/2 lattice model in the second figure. In order to get the volumes right, they must be entered manually, using the set mvol option.