Surface types
From Serpent Wiki
Contents
Elementary surfaces
Notes:
- Elementary surfaces refer here to surfaces that can be represented by a single equation.
Planes
Notes:
- Parametric form of the general plane is assumed if four values are provided in the surface card. With six values the plane is assumed to be defined by three points.
- The positive side for a plane defined by three points is determined by the order in which the points are entered (see the right-hand rule).
| Surface name | Parameters | Surface equation | Description |
|---|---|---|---|
| px | x0 | 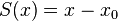
|
Plane perpendicular to x-axis at x = x0 |
| py | y0 | 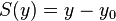
|
Plane perpendicular to y-axis at y = y0 |
| pz | z0 | 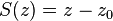
|
Plane perpendicular to z-axis at z = z0 |
| plane | A, B, C, D | 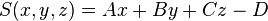
|
General plane in parametric form |
| plane | x1, y1, z1, x2, y2, z2, x3, y3, z3 | General plane defined by three points |
Second-order quadratic surfaces
Notes:
- cyl is the same surface as cylz
- Infinite cylinders use the same names as the truncated cylinders.
- With three values provided in the surface card for cylx, cyly, cylz or cyl the surface is an infinite cylinder. With five values the surface is an truncated cylinder.
| Surface name | Parameters | Surface equation | Description |
|---|---|---|---|
| cylx | y0, z0, r | 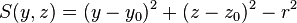
|
Infinite cylinder parallel to x-axis, centred at (y0,z0), radius r |
| cyly | x0, z0, r | 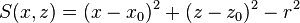
|
Infinite cylinder parallel to y-axis, centred at (x0,z0), radius r |
| cylz, cyl | x0, y0, r | 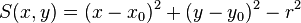
|
Infinite cylinder parallel to z-axis, centred at (x0,y0), radius r |
| cylv | x0, y0, z0, u0, v0, w0, r | 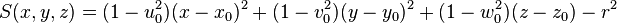
|
Infinite cylinder, parallel to (u0,v0,w0), centred at (x0,y0,z0), radius r |
| sph | x0, y0, z0, r | 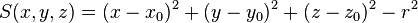
|
Sphere, centred at (x0,y0,z0), radius r |
| cone | x0, y0, z0, r, h | 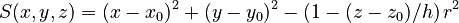
|
Half cone parallel to z-axis, base at (x0,y0,z0), base radius r, height h (distance from base to vertex) |
| quadratic | A, B, C, D, E, F, G, H, I, J | 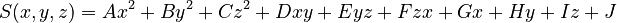
|
General quadratic surface in parametric form |
Non-quadratic surfaces
Notes:
- Serpent can handle circular and elliptical torii. Radii r1 and r2 must be set equal (denoted in the surface equations as r) to describe a circular torus surface.
| Surface name | Parameters | Surface equation | Description | Notes |
|---|---|---|---|---|
| inf | - | 
|
All space | Can not be used in root universe |
| torx | x0, y0, z0, R, r, r | 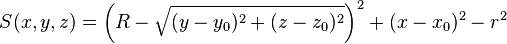
|
Circular torus with major radius R perpendicular to x-axis (revolving radius), centred at (x0, y0, z0), minor radius r (inner radius). | |
| x0, y0, z0, R, r1, r2 | 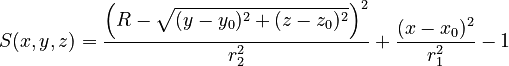
|
Elliptic torus with major radius R perpendicular to x-axis (revolving radius) centred at (x0, y0, z0), vertical (x-)semi-axis r1 and horizontal (y-/z-)semi-axis r2. | ||
| tory | x0, y0, z0, R, r, r | 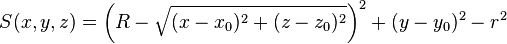
|
Circular torus with major radius R perpendicular to y-axis (revolving radius), centred at (x0, y0, z0), minor radius r (inner radius). | |
| x0, y0, z0, R, r1, r2 | 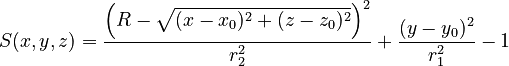
|
Elliptic torus with major radius R perpendicular to y-axis (revolving radius) centred at (x0, y0, z0), vertical (y-)semi-axis r1 and horizontal (x-/z-)semi-axis r2. | ||
| torz | x0, y0, z0, R, r, r | 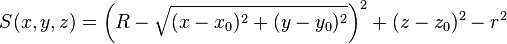
|
Circular torus with major radius R perpendicular to z-axis (revolving radius), centred at (x0, y0, z0), minor radius r (inner radius). | |
| x0, y0, z0, R, r1, r2 | 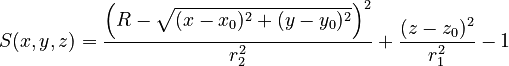
|
Elliptic torus with major radius R perpendicular to z-axis (revolving radius) centred at (x0, y0, z0), vertical (z-)semi-axis r1 and horizontal (x-/y-)semi-axis r2. |
Derived surface types
Notes:
- Derived surfaces refer here to surfaces composed of two or more elementary types.
Truncated cylinders
Notes:
- Truncated cylinders use the same names as the infinite cylinders.
- With five values provided in the surface card for cylx, cyly, cylz or cyl the surface is an truncated cylinder. With three values the surface is an infinite cylinder.
| Surface name | Parameters | Composed of | Description |
|---|---|---|---|
| cylx | y0, z0, r, x0, x1 | Infinite cylinder + two planes | Infinite cylinder parallel to x-axis, centred at (y0,z0), radius r, truncated between [x0, x1] |
| cyly | x0, z0, r, y0, y1 | Infinite cylinder + two planes | Infinite cylinder parallel to y-axis, centred at (x0,z0), radius r, truncated between [y0, y1] |
| cylz, cyl | x0, y0, r, z0, z1 | Infinite cylinder + two planes | Infinite cylinder parallel to z-axis, centred at (x0,y0), radius r, truncated between [z0, z1] |
Regular prisms
Notes:
- All prisms are parallel to z-axis, and they can be rotated using surface transformations.
- Infinite and truncated triangular prisms use the same name, and are composed by three or five planes, respectively. Infinite prism is assumed if three/four values are provided in the surface card tric. With six values the surface is assumed to be a truncated (equilateral) triangular prism.
- Triangular prisms orientation, ori, corresponds to the cardinal direction of the non-aligned vertex of the triangle. Default orientation is North. It follows the scheme: W-S-E-N (W=1, S=2, E=3, N=4).
| Surface name | Parameters | Composed of | Description |
|---|---|---|---|
| tric | x0, y0, d, ori | three planes | Infinite (equilateral) triangular prism parallel to z-axis, centred at (x0,y0), half-width d, orientation ori (optional) |
| x0, y0, d, ori, z0, z1 | five planes | Truncated (equilateral) triangular prism parallel to z-axis, centred at (x0,y0), half-width d, orientation ori, truncated between [z0, z1] | |
| sqc | x0, y0, d | four planes | Infinite square prism parallel to z-axis, centred at (x0,y0), half-width d |
| rect | x0, x1, y0, y1 | four planes | Infinite rectangular prism parallel to z-axis, between [x0, x1] and [y0, y1] |
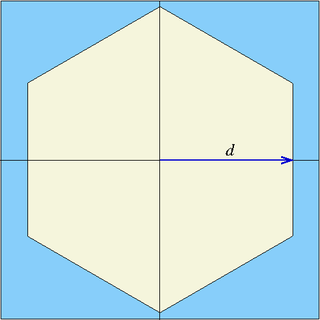
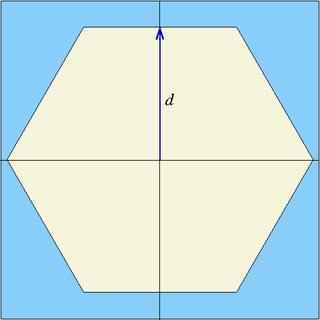
| hexxc | x0, y0, d | six planes | Infinite hexagonal prism parallel to z-axis, centred at (x0,y0), flat surface perpendicular to x-axis, half-width d |
| hexyc | x0, y0, d | six planes | Infinite hexagonal prism parallel to z-axis, centred at (x0,y0), flat surface perpendicular to y-axis, half-width d |
| hexxprism | x0, y0, d, z0, z1 | eight planes | Truncated hexagonal prism parallel to z-axis, centred at (x0,y0), flat surface perpendicular to x-axis, half-width d, truncated between [z0, z1] |
| hexyprism | x0, y0, d, z0, z1 | eight planes | Truncated hexagonal prism parallel to z-axis, centred at (x0,y0), flat surface perpendicular to y-axis, half-width d, truncated between [z0, z1] |
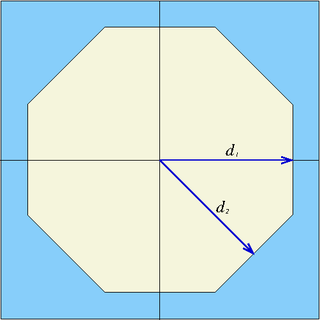
| octa | x0, y0, d1, d2 | eight planes | Infinite octagonal prism parallel to z-axis, centred at (x0,y0), half-widths d1 and d2. If the last value is omitted: d = d1 = d2 |
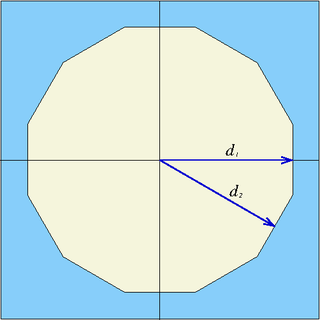
| dode | x0, y0, d1, d2 | twelve planes | Infinite dodecagonal prism parallel to z-axis, centred at (x0,y0), half-widths d1 and d2. If the last value is omitted: d = d1 = d2 |
3D polyhedra
Notes:
- The description of parallelepiped may be wrong.
| Surface name | Parameters | Composed of | Description |
|---|---|---|---|
| cube | x0, y0, z0, d | six planes | Cube, centred at (x0,y0,z0), half-width d |
| cuboid | x0, x1, y0, y1, z0, z1 | six planes | Cuboid, between [x0, x1], [y0, y1] and [z0, z1] |
| ppd | x0, y0, z0, Lx, Ly, Lz, αx, αy, αz | six planes | Parallelepiped, with corner at (x0, y0, z0) and edges of length Lx, Ly and Lz at angles αx, αy and αz (in degrees) with respect to the coordinate axes |
Other derived surface types
| Surface name | Parameters | Description |
|---|---|---|
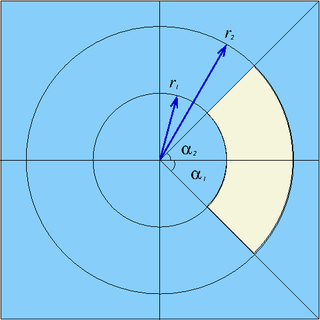
| pad | x0, y0, r1, r2, α1, α2 | Sector from α1 to α2 (in degrees) of a cylinder parallel to z-axis, centred at (x0,y0), between radii r1 and r2 |
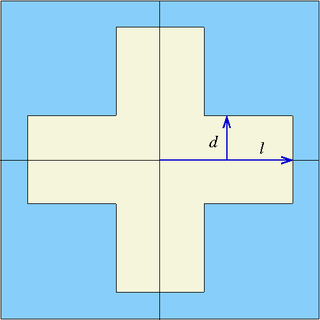
| cross | x0, y0, l, d | Cruciform prism parallel to z-axis, centered at (x0,y0), half-width l, half-thickness d |
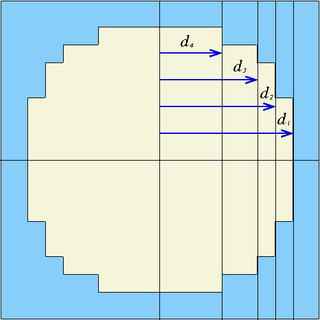
| gcross | x0, y0, d1, d2, ... | Prism parallel to z-axis, centred at (x0,y0), formed by planes at distances dn from the center ("generalized cruciform prism", see figure below) |
| hexxap | x0, y0, wd, dw, a | Surface for simplified modeling of hexagonal fuel assembly angle pieces. Consists of two infinite hexagonal prisms parallel to z-axis, centered at (x0, y0), flat surfaces perpendicular to x-axis, with the outer hexagon having outer half-width of wd, and the surface perpendicular thickness is dw (the inner hexagon half width is wd - dw), and each half-section of each angle piece with width of a, measured from the tip of the angle piece angle to the flat surface of the angle piece. |
| hexyap | x0, y0, wd, dw, a | Surface for simplified modeling of hexagonal fuel assembly angle pieces. Consists of two infinite hexagonal prisms parallel to z-axis, centered at (x0, y0), flat surfaces perpendicular to y-axis, with the outer hexagon having outer half-width of wd, and the surface perpendicular thickness is dw (the inner hexagon half width is wd - dw), and each half-section of each angle piece with width of a, measured from the tip of the angle piece angle to the flat surface of the angle piece. |
| involute | x0, y0, r0, θ1, θ2, r1, r2 | Involute parallel to z-axis, centred at (x0,y0), involute radius r0, and involute starting angle θ0 (defined by θ1 and θ2, first and second involute angles, respectively, in radians), and, limited by an inner and an outer cylinder with radii r1 and r2, respectively.[1] |
| vessel | x0, y0, r, z1, z2, h1, h2 | Vessel-like surface based on a infinite cylinder parallel to z-axis centred at (x0, y0), radius r, truncated between [z1,z2], and two semi-ellipsoids: [bottom] centred at (x0,y0,z1), with semi-axes r, r, h1, truncated at z1; [top] centred at (x0,y0,z2), with semi-axes r, r, h2, truncated at z2. If the last value is omitted: h = h1 = h2 |
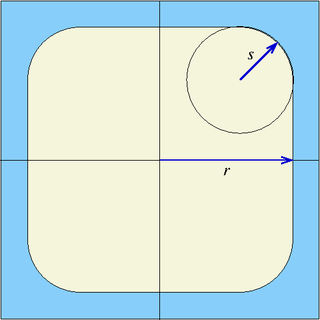
Rounded corners
Infinite prisms:
- sqc
- hexxc
- hexyc
- cross
Allow defining rounded corners. The radius is then provided as the last surface parameter (s in figure below):
MCNP-equivalent surfaces
Notes:
- Additional surfaces included to simplify input conversion between Serpent and MCNP.
- For description, see Chapter 5, Section 5.3 of the MCNP6.3 User Manual.[2]
| Surface name | Equivalent surface in MCNP |
|---|---|
| box | BOX |
| ckx | K/X |
| cky | K/Y |
| ckz | K/Z |
| mplane | P (form defined by three points) |
| rcc | RCC |
| x | X |
| y | Y |
| z | Z |
User-defined surfaces
Notes:
- Remember to make a backup of your subroutine before installing new updates.
- If you have a working surface routine that might be useful for other users as well, contact the Serpent team and we'll include it in the next update as a built-in type.
| Surface name | Parameters | Description |
|---|---|---|
| usr | p1, p2, ... | User-defined surface, implemented in source file "usersurf.c". The subroutine receives the number and list of surface parameters as input. Instructions are included as comments in the source file. |