Stochastic Implicit Euler burnup scheme
The Stochastic Implicit Euler (SIE) burnup scheme is an alternative burnup scheme that can be used if the traditional predictor-corrector burnup schemes in Serpent exhibit unstable behavior.
Background
The theoretical background of the SIE scheme is described in [1]
Input
The SIE burnup scheme can be chosen with the set sie input card. The number of iterations for each burnup steps can be specified.
Some additional input options that many times are combined with the set sie card are set fsp for passing the fission source from the end of previous neutron transport solution to the beginning of the next one, and set cpop to use an alternate (typically lower) neutron population for the SIE iteration (compared to the neutron population used on the initial predictor step.
Implementation
For burnup calculations, Serpent needs to evaluate the one group flux 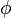 for each depletion region and one group fission/transmutation cross sections
for each depletion region and one group fission/transmutation cross sections 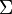 for each fission/transmutation reaction of each nuclide.
for each fission/transmutation reaction of each nuclide.
These can then be used for calculating the reaction rates required for assembling the burnup matrix 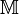 . The following algorithmic description uses
. The following algorithmic description uses 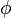 to refer to both the one group burn flux and the one group cross sections.
to refer to both the one group burn flux and the one group cross sections.
- The following description will use BOS and EOS to refer to beginning-of-step and end-of-step quantities respectively.
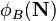 refers to running a neutron transport simulation using nuclide densities
refers to running a neutron transport simulation using nuclide densities 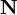 .
.![\exp \left[ \mathbb{M}(\phi) \Delta t\right] \mathbf{N}](/mediawiki/images/math/a/0/3/a036fab0d80b5d2d531d837f8520f709.png) refers to executing a depletion solution with burnup matrix
refers to executing a depletion solution with burnup matrix 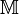 using one group fluxes and cross sections
using one group fluxes and cross sections 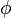 , timestep
, timestep 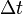 and initial nuclide densities
and initial nuclide densities 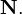
| 1: | input: 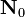
|
Start from initial nuclide concentrations. | ||
| 2: | 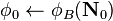
|
Calculate BOS 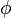 using initial BOS nuclide densities. using initial BOS nuclide densities.
| ||
| 3: | for 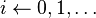 do do
|
Loop over burnup points. | ||
| 4: | ![\mathbf{N}_{i+1}^{(0)} \leftarrow \exp \left[ \mathbb{M}(\phi_{i}) \Delta t\right] \mathbf{N}_{i}](/mediawiki/images/math/2/5/3/25389338a07bf23fb750b5ab78ff2720.png)
|
Obtain EOS nuclide densities by burning forward (predictor) using previously obtained BOS 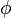 . .
| ||
| 5: | for 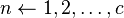 do do
|
Loop over (corrector) iterations for current burnup point. | ||
| 6: | 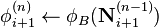
|
Calculate estimate for EOS 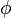 using current estimate of EOS nuclide densities. using current estimate of EOS nuclide densities.
| ||
| 7: | 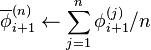
|
Relax (average) the EOS 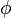 over all EOS estimates obtained for current burnup point. over all EOS estimates obtained for current burnup point.
| ||
| 8: | ![\mathbf{N}_{i+1}^{(n)} \leftarrow \exp [ \mathbb{M}(\overline{\phi}^{(n)}_{i+1}) \Delta t] \mathbf{N}_{i}](/mediawiki/images/math/f/4/a/f4af227a0237be86585911d560330d2a.png)
|
Obtain the next estimate for EOS nuclide densities by re-burning from BOS nuclide densities (corrector) using relaxed (averaged) EOS 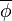 . .
| ||
| 9: | end for | Loop to next iteration for current burnup point or go forward if all iterations have been simulated. | ||
| 10: | 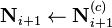
|
The last obtained EOS nuclide densities will be the final ones and serve as BOS densities for the next step. | ||
| 11: | 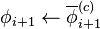
|
The last obtained relaxed EOS 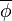 will serve as the final EOS will serve as the final EOS 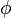 for current step and as BOS for current step and as BOS 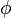 for the next step. for the next step.
| ||
| 12: | end for | Loop to next burnup step or finish calculation. | ||
| xx | xx | |||
To put the burnup scheme into simple terms: On each burnup step, there is first a predictor step, where EOS nuclide densities are obtained from BOS nuclide densities by burning forward using the BOS fluxes and cross sections (in an explicit Euler manner) obtained either from an initial neutron transport calculation (only on first step) or from the EOS fluxes and cross sections of the previous burnup step.
This predictor step is followed by a number of corrector iterations. In each iteration, the EOS fluxes and cross sections are first obtained through a neutron transport calculation using the current estimate for EOS nuclide densities. Then the estimates for the EOS fluxes and cross sections are relaxed (averaged) over all previous iterations simulated for the current burnup point. A new estimate for the EOS nuclide densities is then obtained by burning the interval again (in implicit Euler manner) using the BOS nuclide densities and the relaxed EOS fluxes and cross sections.
After the specified number of corrector iterations has been executed, the final EOS nuclide densities and relaxed EOS fluxes and cross sections serve as the BOS nuclide densities and BOS fluxes and cross sections for the predictor step of the next burnup interval.
It should be noted that no neutron transport solution is actually calculated using the final EOS nuclide densities. This means that any results (k-eff, fluxes, etc.) obtained during the last corrector iteration do not actually represent the final estimate for the results for that specific burnup point. The SIE burnup scheme is intended to be used to obtain nuclide densities for each burnup point that can be saved using restart files and after the burnup calculation, any number of detectors etc. can be set up and the interesting results can be calculated for each of the burnup points e.g. by loading the nuclide densities from the restart file manually using set rfr.
Usage
See:
Noteworthy things
- No neutron transport solution is actually calculated using the final concentrations for a certain point.
References
- ^ Dufek, J., Kotlyar, D. and Shwageraus, E. "The stochastic implicit Euler method – A stable coupling scheme for Monte Carlo burnup calculations", Ann. Nucl. Energy, 60 (2013) 295-300