Coupled multi-physics calculations
Serpent 2 has been written with multi-physics applications in mind. The capability to model arbitrarily detailed density and temperature distributions means that most temperature and density distributions given by e.g. thermal hydraulics or CFD solvers can be brought into Serpent using one of the multi-physics interface file formats without loss of detail. There are dedicated routines for controlling the iteration between the neutronics solver (Serpent) and the solver(s) for the coupled fields in order to obtain the converged coupled solution.
Contents
Multi-physics interface
The universal multi-physics interface can be used to easily bring in temperature and density solutions from any external solvers. With the multi-physics interface, the solution fields (temperature/density) can be overlaid on top of the base geometry model without having to make additional modifications (such as defining multiple materials with different temperatures) to the input.
See the detailed description: multi-physics interface.
External coupling
Internal solvers
Serpent is able to internally couple to the FINIX fuel behavior module that can be licensed separately from VTT.
Iteration
The coupled calculation routines in Serpent have been designed with the Picard-iteration style multi-physics calculations in mind (also referred to as tight coupling in some sources). In this iteration type, the separate solvers can be iterated subsequently for a certain state-point until a convergence is reached, after which the simulation will move to the next time point.
The maximum number of iterations between the different solvers at each time point can be specified with the set ccmaxiter input-option.
Power relaxation
Serpent relaxes the power distribution calculated in the iterations using the stochastic approximation based method[1], where the power distribution at iteration 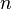 is calculated by
is calculated by
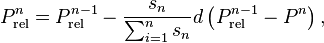
where 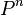 is the unrelaxed power distribution tallied on iteration
is the unrelaxed power distribution tallied on iteration 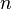 ,
, 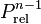 is the relaxed power distribution after the previous iteration,
is the relaxed power distribution after the previous iteration, 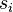 is the active neutron population simulated on iteration
is the active neutron population simulated on iteration 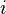 and
and  is an underrelaxation factor that can be defined by the set relfactor option.
is an underrelaxation factor that can be defined by the set relfactor option.