Transient simulations

This page outlines the usage instructions for the methodology in Serpent to conduct time dependent simulations starting from a criticality source. These capabilities have been developed for transient calculations starting from a known critical system in steady state conditions. For information about external/fixed source simulations with population control see: Dynamic external source simulation mode

Transient analyses with Serpent currently have to be executed in two parts:

1. A criticality source simulation to generate the steady state neutron and delayed neutron precursor sources for the time dependent simulation.
2. A time dependent simulation to model the time evolution of the system starting from the steady state source distributions.

Generating the steady state source distributions

Input

Generating the initial source for the dynamic simulation is done with a criticality source simulation (see the model input). The only modification required to an existing input is the addition of one line:

set savesrc FILEPATH [PN PP NX NY NZ]

The [FILEPATH] argument tells Serpent, where to save the generated source distributions. Serpent will actually generate four source files:

• [FILEPATH].main - containing general information of the generated source
• [FILEPATH].prec - containing a precursor source tallied on a cartesian mesh
• [FILEPATH].live - containing the live neutron source (binary)
• [FILEPATH].precpoints - containing a point-wise precursor source (binary)

The other arguments are optional: PN and PP (numbers between [0,1]) can be used to adjust the probability store any single neutron or precursor to the source respectively. The default values are 1.0 for each. PN has to be adjusted a smaller value in many simulations. Since the probability to store a live neutron in any interaction has an inverse dependence on the cross section used to sample the path, the way the probability is calculated can lead to larger than unity probabilities for some interactions. In these cases Serpent will print out a warning:

***** Fri Feb  5 11:58:16 2016 (seed = 1454666276)
Warning message from function WriteSourceFile:

P larger than 1 (1.630892E+00)

PN should be then adjusted to make the saving probabilities smaller than one (PN is directly used to multiply the saving probability). PN linearly affects the number of neutrons being saved, so making it too small means that a large amount of neutrons have to be simulated to produce an adequate number of source points. Another way to tackle the P larger than 1 problem is to decrease the maximum mean free path used by Serpent by setting lower values for set cfe: Halving the default scoring distance for neutrons should be a good starting point for lowering the sampled P values without storing less neutrons.

A smaller than unity PP can be set if, for some reason, the number of point-wise precursors that are saved has to be reduced.

NX, NY and NZ are optional parameters that can be used to set the size of the cartesian mesh used to tally the precursor populations (1x1x1 by default). If the point-wise precursor tracking will be used in the time dependent simulation, this can be left to the default size.

Background on PN

We want to have our live neutron source to be representative of the neutron distribution in our system at the time of the beginning of our transient. One way to visualize this is to have our system in its steady state and at a random moment take a snapshot of all the neutrons in the system. Each neutron is caught in this snapshot at a random time in their life: Some have just been born while others may have already thermalized.

To obtain such a source from a Monte Carlo simulation we have to store neutrons at random times during their life. If we don't want to slow down our criticality source calculation by stopping our neutrons at various times in the simulation we can save neutrons at their tentative interaction sites: After a path-length has been sampled for a neutron and it has been transported to a new (possible) interaction site we can store information (such as position, velocity and energy) on the neutron to a source file.

These tentative interaction sites are not, however, distributed uniformly in time or space. If we would store neutrons at each interaction site with a fixed probability, we would obtain too many fast neutrons (fast speed leads to more interactions per unit time than slow speed) and too many neutrons from materials with a large macroscopic cross section (large macroscopic cross section leads to more interactions).

To use a more rigorous derivation, the mean path-length between two interactions (mean free path) for a neutron with energy E travelling over a path, where the interaction probability is constant over the path length, is

$\lambda_{\mathrm{mean}}(E) = \frac{1}{\Sigma_{\mathrm{tot}}(E)}$,

where $\Sigma_{\mathrm{tot}}(E)$ is the total macroscopic cross section over the path. The time it takes for the neutron to travel this path length gives the mean time between two interactions

$t_{\mathrm{mean}}(E) = \frac{\lambda_{\mathrm{mean}}(E)}{v(E)} = \frac{1}{\Sigma_{\mathrm{tot}}(E)v(E)}$,

where $v(E)$ is the velocity of the neutron. This means that the mean interaction frequency depends on the energy of neutrons as

$f_{\mathrm{mean}}(E) = \frac{1}{t_{\mathrm{mean}}(E)} = \Sigma_{\mathrm{tot}}(E)v(E)$.

If we want to save neutrons at interaction sites and want the saved neutrons to have been sampled uniformly in time, we'll want to have the probability to save a given neutron at an interaction site to be

$P \propto \frac{1}{f_{\mathrm{mean}}(E)} = \frac{1}{\Sigma_{\mathrm{tot}}(E)v(E)}$.

We'll want the probability to be less than one, which means that we'll use an additional normalization constant A:

$P = A \frac{1}{\Sigma_{\mathrm{tot}}(E)v(E)}$.

Furthermore, in non-analog simulations some of our neutrons might have a non-unity weight w, meaning that they represent a larger or a smaller group of neutrons than the average neutron. We'll take this in account as an additional weighting term for the probability:

$P = A \frac{w}{\Sigma_{\mathrm{tot}}(E)v(E)}$.

When delta tracking is used, the cross section used to sample each path length may be larger than the local macroscopic total cross section. This is taken in account by using the path length sampling cross section $\Sigma_{\mathrm{path}}(E)$ instead of the local total cross section $\Sigma_{\mathrm{tot}}(E)$:

$P = A \frac{w}{\Sigma_{\mathrm{path}}(E)v(E)}$.

The final question is then how to choose the normalization constant A. Based on the expression above, it is evident that if we choose

$A = \frac{1}{\max \frac{w}{\Sigma_{\mathrm{path}}(E)v(E)}}$,

where the maximum is taken over all neutron energies and the whole geometry, the probability will always be smaller than unity. The minimum velocity of the neutrons is known based on the minimum energy of neutrons (minimum of cross section data). However, the minimum path length sampling cross section is slightly more tricky. In, e.g. void regions the total cross section is zero, which would lead to an infinite value of A. However, Serpent uses an internal minimum cross section for the path length sampling (set cfe), which means that the path length sampling cross section should always be greater than zero.

The current implementation sets

$A = P_{N} v_{\mathrm{min}}$,

where $v_{\mathrm{min}}$ is the minimum velocity for neutrons and $P_N$ is the parameter PN that can be set by user and needs to cover the variation in minimum path length sampling cross section and the neutron weight. The PN parameter may become obsolete at some point in the future due to better pre-calcuation of the constant A.

Output

.main-file

The .main-file contains general information of the saved neutron and precursor sources.

nPop nPopErr
nTime nGroups nSpatial0 nSpatial1 nSpatial2
time
lambda1 lambda2 ... lambdanGroups

The .main-file contains the total neutron population of the system on the first line accompanied with it's estimated relative standard error. Serpent uses this to set the initial power level of the dynamic simulation to match that of the criticality source simulation.

The second line contains information about the binning of the precursor population. The number of the precursor groups is equal to the number of unique delayed neutron groups in the simulation.

The third line contains the simulation time the saved source matches. This will only be non-zero if using set savesrc in a time dependent simulation.

The fourth line contains the decay constants of the delayed neutron groups. Serpent uses these to check that the same group structure is being used in the criticality source simulation and the time dependent simulation.

.prec-file

The .prec-file contains the group-wise precursor populations tallied on the regular mesh. With point-wise precursors they are only used to set the normalization of the precursors. Each line contains a single tally bin:

iTime iGroup iSpatial value error

where

iTime	: the time bin index (0 = beginning of simulation, largest index = end of simulation)
iGroup	: the delayed neutron group index
iSpatial	: the spatial bin index
value	: the stable precursor population in the bin
error	: the estimated relative standard error of the population

.live-file

The .live-file is a binary file containing neutrons stored at random interactions (uniformly distributed in time) during the active cycles of the criticality source simulation. Each neutron consists of nine values each taking eight bytes (64 bits). The values are (in order):

1. x-coordinate (cm)
2. y-coordinate (cm)
3. z-coordinate (cm)
4. u : Directional cosine with respect to the x-axis
5. v : Directional cosine with respect to the y-axis
6. w : Directional cosine with respect to the z-axis
7. E : Neutron energy (MeV)
8. wgt : Statistical weight
9. t : Simulation time

Since each neutron takes

9*sizeof(double) = 9*8 = 72 

bytes of disk space, the number of stored neutrons can be calculated by dividing the file size (in bytes) by 72.

.precpoints-file

The .precpoints-file is a binary file containing delayed neutron precursors stored using an implicit estimator during the active cycles of the criticality source simulation. Each precursor also takes up

9*sizeof(double) = 9*8 = 72

bytes of disk space, which means that the number of stored precursors can be calculated from the file size the same way as with live neutrons. The nine values stored for each precursor are

1. x-coordinate (cm)
2. y-coordinate (cm)
3. z-coordinate (cm)
4. Always 1 (not used)
5. Always 0 (not used)
6. Always 0 (not used)
7. Either 1 (dynamic simulations) or energy of producing neutron (criticality source simulations) (not used)
8. wgt : Statistical weight
9. g : Precursor group

Important notes

• The system should be as close to criticality as possible as any deviations result in errors in the live neutron source (due to the k-eigenvalue iteration only being accurate in critical systems) and in the precursor source (since the stable concentrations are calculated assuming steady state).

• Implicit reaction modes will affect the weight distribution of the neutron population, which may have adverse effects for statistics in some cases. The implicit reaction modes can be turned off by first turning off the group constant generation (set gcu -1) and then turning off the implicit reaction modes (set impl 0 0 0).

Running the time dependent simulation

Basic approach in the time-dependent simulations

Serpent tracks both neutrons and precursors through time in a continuous manner (without any time-discretization). The initial neutron and precursor source in the beginning of the simulation is known based on the source generation simulation.

The transient simulation can be divided into sub-intervals for population control purposes. In the simplest case the transient can be simulated as a single time-interval.

The basic process for each time-interval is as follows:

1. Create the primary source for the time-interval:
   1. Calculate the live neutron population at the beginning of the interval. This is done either from the initial neutron source or from the current neutron banks.
   2. Calculate the decay of precursor tallies based on the decay law to
      • Determine the delayed neutron population emitted from the tallies during the interval
      • Determine and store the initial value of each tally at end-of-interval.
   3. Divide the initial source points between live neutrons and delayed neutrons emitted from precursors based on proportion of the two populations.
   4. Population control the live neutron source to the required number.
   5. Sample the emission of the required number of delayed neutrons from existing precursors
2. Simulate the primary particles and any secondary/further particles that emitted during the time-interval.
   • Tally the precursor production during the neutron tracking.
3. Store the neutrons that reach the end of the time interval. Add the precursors that were produced and survived until the end of the interval to the end-of-interval precursor tallies.
4. Start again from 1.

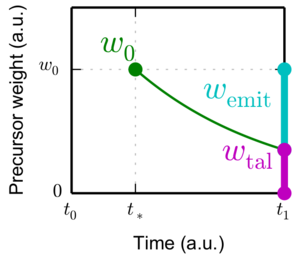
For the new precursors produced during the time-interval, only a part of their weight survives until the end of the time-interval due to decay happening during the interval:

In the picture above, the initial produced precursor weight in an interaction happening at time $t_*$ is $w_0$. Only a part of the weight survives until the end of the interval to be added to the end-of-interval tallies:

$w_{\mathrm{tal}} = w_0e^{-\lambda_g (t_* - t_0)}$.

The remaining part decays during the interval and should be emitted as a delayed neutron

$w_{\mathrm{emit}} = w_0\left(1-e^{-\lambda_g (t_* - t_0)}\right)$.

As $w_{\mathrm{emit}}$ is typically small compared to $w_0$ the delayed neutron to be emitted is subjected to Russian roulette to either increase its weight to a more reasonable level or not emit it at all.

Input

Small modifications should be made to the criticality source input in order to run the time dependent simulation:

1. The time binning of the simulation should be created with the tme card.
2. The simulated population should be set with the set nps option and the simulation time binning should be provided here.
3. A previously generated steady state source should be linked with the set dynsrc option.

To set up the delayed neutrons you should just link the source generated previously with the

set dynsrc PATH [ MODE ]

input option, where the parameters are

PATH	: The path of the previously generated source file (without the .main suffix)
MODE	: Precursor tracking mode (0 = mesh based, 1 = point-wise)

The four separate source files should be found PATH.main, PATH.prec, PATH.live and PATH.precpoints.

Notes:

• The geometry and the material compositions of the system can be modified before the time dependent simulation to perturb the system. However, the neutron and precursor source distributions will be overlaid to the new geometry as is, without any modifications.
• The neutron and precursor source at the end of the time dependent simulation can also be saved using the set savesrc input option. A file-path different from the initial source file-path should be defined, in order not to overwrite the initial source distribution.
• If the neutron and precursor source linked with the set dynsrc input option is from a previous time dependent simulation and thus corresponds to a nonzero simulation time, the time binning of this simulation should start from the end time of the previous simulation.
• Detector output in time dependent calculations is integrated with respect to time.

Detector output in transient simulations

The detector output values in transient simulations are time-integrated values. For example, detector response -8 (fission power deposition) will yield the fission energy deposition in Joules rather than Watts.

The detector output in transient simulations works differently depending on whether the transient simulation is coupled (using set comfile or set ppid or by using the FINIX fuel behavior module) or not.

1. In non-coupled transient simulations the simulation proceeds by first simulating the first neutron batch through all of the time-intervals before simulating the next batch.

2. In coupled transient simulations the simulation proceeds by first simulating all of the neutron batches through the first time-interval before simulating the next time-interval.

Due to the difference in the simulation process, the detector results are also collected differently:

1. In non-coupled transient simulations the detector results are collected from all of the time-intervals and the [input]_det.m file will contain results from all time-intervals.

2. In coupled transient simulations all statistics, such as detector results are cleared between time-intervals, which means that during the simulation of a certain time-interval only the detector bins that lie in that interval get non-zero scores.

In coupled transient simulations Serpent produces one detector output file for each time-interval. [input]_det0.m will contain detector scores from the first time-interval, [input]_det1.m from the second time-interval and so on.

This means that if you want to get the detector results using a time-binning corresponding to the simulation time-intervals you don't actually need to specify any time-binning for the detector as each of the input_det<N>.m files will contain the results for one time-interval. If you want to obtain results using a finer grid than the one used for simulation time-intervals you can specify that for the detectors and combine the results from the [input]_det<N>.m files during post-processing.

Input examples

• Infinite homogeneous LWR-like reactor transient example
• 3D BWR assembly transient example

Publications and presentations

• Presentation on delayed neutron emission model for transients in PHYSOR2016
• Presentation on transient simulations in UGM 2016