Coupled multi-physics calculations

Power relaxation

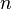Serpent relaxes the power distribution calculated in the iterations using the stochastic approximation based method, where the power distribution at iteration $n$ is calculated by

$P_{\mathrm{rel}}^{n} = P_{\mathrm{rel}}^{n-1} - \frac{s_{n}}{\sum_{i = 1}^{n} s_{n}} d \left(P_{\mathrm{rel}}^{n-1} - P^{n}\right),$

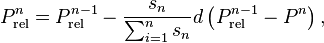
where 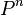$P^{n}$ is the unrelaxed power distribution tallied on iteration 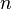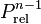$n$, $P_{\mathrm{rel}}^{n-1}$ is the relaxed power distribution after the previous iteration, 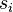$s_{i}$ is the active neutron population simulated on iteration 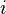$i$ and $d$ is an underrelaxation factor that can be defined by the set relfactor option.