Difference between revisions of "Result estimators"
(→Collision flux estimator (CFE)) |
(→Collision flux estimator (CFE)) |
||
| Line 79: | Line 79: | ||
and <math>f</math> is the response function and <math>\Sigma</math> is the cross section that | and <math>f</math> is the response function and <math>\Sigma</math> is the cross section that | ||
| − | was used for sampling the path length. It should be noted that with [[Delta- and surface-tracking# | + | was used for sampling the path length. It should be noted that with [[Delta- and surface-tracking#Transport algorithms in Monte Carlo simulation|delta-tracking]] this cross section is not necessarily the physical material total. |
=== Track-length estimator (TLE) === | === Track-length estimator (TLE) === | ||
Revision as of 16:47, 19 November 2015
The Monte Carlo transport simulation is run to obtain statistical estimates for integrals of the form:
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.):
where $f$ is a response function that can be evaluated at an arbitrary position
of the phase space, most typically a reaction cross section. These estimates
are based on the collection of simulated events (collisions, track-lengths,
surface crossings, etc.) that occur during the course of the simulated
random walk.
The estimates can be divided into:
- Analog estimates, based on recorded simulated physical events
- Implicit estimators, based the expected frequency of events
Implicit estimators are derived from analog estimators, with the purpose of obtaining better statistics.
Contents
Analog estimators
Analog estimates are the most straightforward way to obtain physical results from the Monte Carlo transport simulation. Each particle history consists of a number of events containing relevant information on the transport process, which can be counted as-is, for example:
- Collisions
- Sampled reactions
- Crossed surfaces
- Neutrons emitted in fission
The integration domain is defined by separating the scores into different bins based on particle position, energy and time (and direction of motion). For example:
- Fission rate in a specific fuel pin -- count the number of simulated fission events in that fuel pin (integration over specific volume)
- Thermal neutron absorption in coolant -- count the number of neutrons absorbed in the coolant with energy in the thermal region (integration over specific volume and energy)
- Total fission rate as function of time -- count the number of fissions, and place the results in successive bins depending on the time of the event (integration over specific time)
These examples also illustrate the fact the results are always integrated over the variables.
The analog estimators used by Serpent 2 are listed below.
Analog estimate of keff
Analog reaction rate estimators
Surface flux and current detectors
Implicit estimators
Implicit estimators are derived from analog estimators, but instead of scoring events that actually occured during the simulation, the estimates are based on the expected occurrance of the evens. The implicit estimators used in Serpent 2 are listed below.
Collision flux estimator (CFE)
Implicit estimators are best understood by considering
the collision estimate of particle flux (CFE). When a collision occurs at a given position,
the probability of sampling reaction 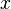 is the ratio of the reaction cross section to material total:
is the ratio of the reaction cross section to material total:
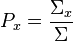
The probability is the same whether the reaction was actually sampled or not,
so counting 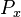 as the result estimate means that the
overall score reflects the statistically expected number of reactions
as the result estimate means that the
overall score reflects the statistically expected number of reactions 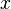 .
.
Since the total number of collisions is always greater than or equal to the number of sampled reactions, the implicit estimator gives better statistics. The overall score is given by the sum over all collisions:
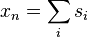
where the CFE is written as:
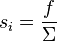
and 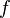 is the response function and
is the response function and 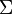 is the cross section that
was used for sampling the path length. It should be noted that with delta-tracking this cross section is not necessarily the physical material total.
is the cross section that
was used for sampling the path length. It should be noted that with delta-tracking this cross section is not necessarily the physical material total.