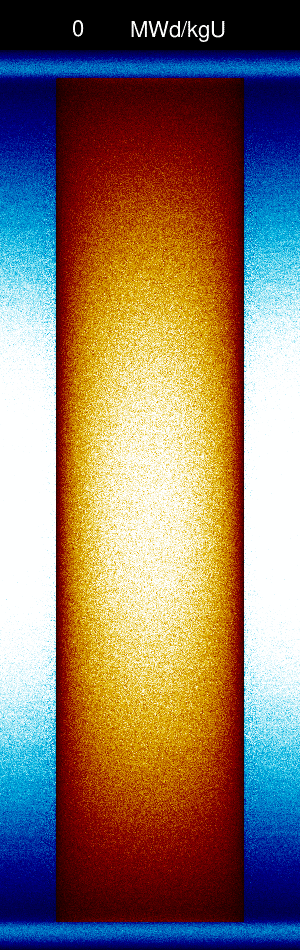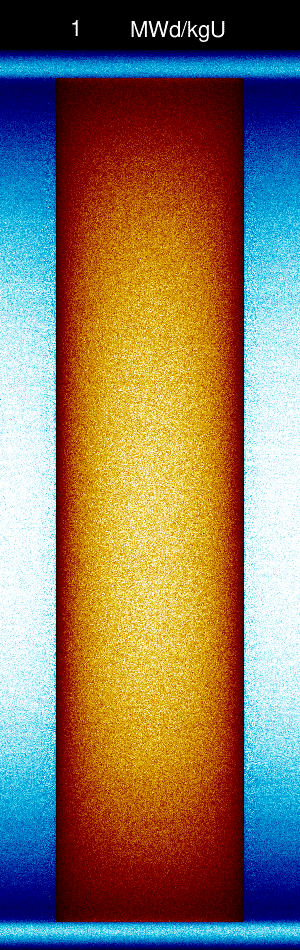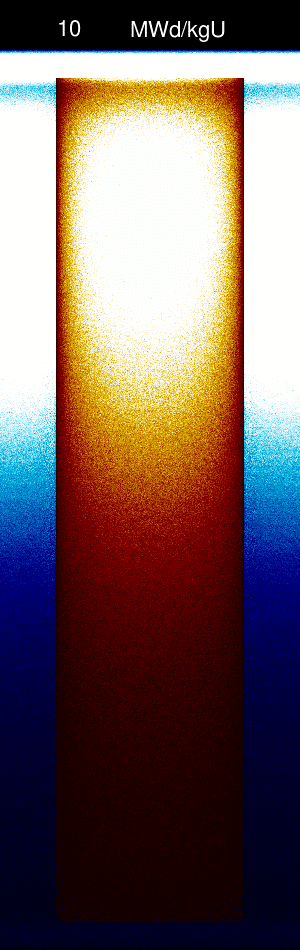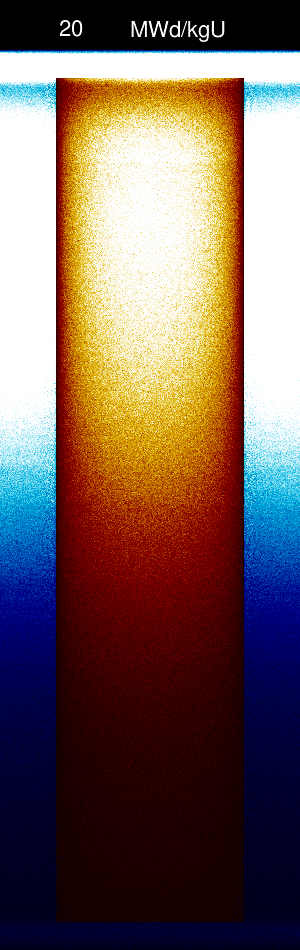Difference between revisions of "Unstable 3D pin-cell burnup problem"
(→Unstable solution using explicit Euler's method) |
(→Unstable solution using explicit Euler's scheme) |
||
| Line 130: | Line 130: | ||
== Unstable solution using explicit Euler's scheme == | == Unstable solution using explicit Euler's scheme == | ||
| + | |||
| + | [[File:UnstableCEmeshAnimation.gif|frameless|300px|yz-meshplot of 3D pin cell problem as a function of burnup.]] | ||
== Unstable solution using predictor-corrector scheme == | == Unstable solution using predictor-corrector scheme == | ||
Revision as of 13:12, 29 September 2017
In certain burnup problems such as long, axially symmetric 3D assemblies or fuel rods or large symmetric core geometries traditional Monte Carlo burnup schemes may run into instabilities[1][2]. This page describes the simulation of one such case first using the traditional burnup schemes (to showcase the instability) and then using a stable burnup scheme.
Contents
Problem description
Base input for unstable 3D pin-cell problem
/***************** ** Run options ** *****************/ % --- 50k neutrons per cycle, 100 inactive cycles set pop 20000 1000 200 % --- 200 W/cm linear power set power 60000 /************************* ** Geometry definition ** *************************/ % --- Fuel Pin definitions: pin p1 fuel 0.47 void 0.48 clad 0.54 cool % --- Lattice lat l1 1 0.0 0.0 1 1 1.5 p1 % --- Surrounding surfaces: % Boundary of geometry: surf 3 cuboid -0.75 0.75 -0.75 0.75 -160 160 % Lower boundary of fuel surf 4 pz -150 % Upper boundary of fuel surf 5 pz 150 % --- Cell definitions: % Active fuel pin cell 3 0 fill l1 -3 4 -5 % Coolant below active fuel (bottom reflector) cell 4 0 cool -3 -4 % Coolant above active fuel (top reflector) cell 5 0 cool -3 5 % outside world cell 99 0 outside 3 % Outside world % --- Reflective boundary conditions in XY, black in Z: set bc 3 3 1 /************************** ** Material definitions ** **************************/ % --- Fuel material (4.85 % enrichment): mat fuel -10.283 vol 208.19 rgb 200 200 125 92235.09c 0.016166667 92238.09c 0.317166667 8016.09c 0.666666667 % --- Cladding (Zr-4) mat clad -6.56000E+00 rgb 180 180 180 8016.06c -1.19276E-03 8017.06c -4.82878E-07 24050.06c -4.16117E-05 24052.06c -8.34483E-04 24053.06c -9.64457E-05 24054.06c -2.44600E-05 26054.06c -1.12572E-04 26056.06c -1.83252E-03 26057.06c -4.30778E-05 26058.06c -5.83334E-06 40090.06c -4.97862E-01 40091.06c -1.09780E-01 40092.06c -1.69646E-01 40094.06c -1.75665E-01 40096.06c -2.89038E-02 50112.06c -1.27604E-04 50114.06c -8.83732E-05 50115.06c -4.59255E-05 50116.06c -1.98105E-03 50117.06c -1.05543E-03 50118.06c -3.35688E-03 50119.06c -1.20069E-03 50120.06c -4.59220E-03 50122.06c -6.63497E-04 50124.06c -8.43355E-04 % --- Coolant: mat cool -0.75 moder lwtr 1001 rgb 50 50 255 1001.06c 0.666666667 8016.06c 0.333333333 % --- Thermal scattering data for light water: therm lwtr lwj3.11t
The base input for the problem is given above. The input describes a 300 cm long fuel rod in infinite lattice geometry. Axially the fuel rod is reflected from top and bottom with 10 cm water layers after which a black boundary condition is applied. The radial geometry is shown here:
Let's say that we want to calculate the axial power distribution and flux distribution using 100 axial bins over the active fuel length at burnups between 0 MWd/kgU and 20 Mwd/kgU. In order to capture the axial burnup distribution we will divide the fuel material axially into a rather small number of division zones (10) using the div card.
Unstable solution using explicit Euler's scheme
Unstable solution using predictor-corrector scheme
Stable solution using SIE burnup scheme
Stable solution using a symmetry boundary
References
- ^ Dufek, J. and Hoogenboom, E. "Numerical Stability of Existing Monte Carlo Burnup Codes in Cycle Calculations of Critical Reactors", Nucl. Sci. Eng., 162 (2009) 307-311
- ^ Dufek, J. et al. "Numerical stability of the predictor–corrector method in Monte Carlo burnup calculations of critical reactors", Ann. Nucl. Energy, 56 (2013) 34-38