Difference between revisions of "Stochastic Implicit Euler burnup scheme"
(→Input) |
(→Implementation) |
||
| Line 12: | Line 12: | ||
== Implementation == | == Implementation == | ||
| + | |||
| + | For burnup calculations, Serpent needs to evaluate the one group flux <math>\phi</math> for each depletion region and one group fission/transmutation cross sections <math>\Sigma</math> for each fission/transmutation reaction of each nuclide. | ||
| + | |||
| + | These can then be used for calculating the reaction rates required for assembling the burnup matrix <math>\mathbb{M}</math>. The following algorithmic description uses <math>\phi</math> to refer to both the one group burn flux and the one group cross sections. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |'''1:''' | ||
| + | |colspan="3"| input: <math>\mathbf{N}_{0}</math> | ||
| + | | Start from initial nuclide concentrations. | ||
| + | |- | ||
| + | |'''2:''' | ||
| + | |colspan="3"|<math>\phi_{0} \leftarrow \phi_{B}(\mathbf{N}_{,0})</math> | ||
| + | | Calculate <math>\phi</math> using initial nuclide concentrations. | ||
| + | |- | ||
| + | |'''3:''' | ||
| + | |colspan="3"|'''for''' <math>i \leftarrow 0,1,\ldots </math> '''do''' | ||
| + | | Loop over burnup points. | ||
| + | |- | ||
| + | |colspan="2"|'''4:''' | ||
| + | |colspan="2"|<math> \mathbf{N}_{i+1}^{(0)} \leftarrow \exp \left[ \mathbb{M}(\phi_{i}) \Delta t\right] \mathbf{N}_{i}</math> | ||
| + | | Burn forward (predictor) using previously obtained BOS <math>\phi</math>. | ||
| + | |- | ||
| + | |colspan="2"|'''5:''' | ||
| + | |colspan="2"| '''for ''' <math>n \leftarrow 1,2,\ldots, c</math> '''do''' | ||
| + | | Loop over iterations for current burnup point. | ||
| + | |- | ||
| + | |colspan="3"|'''6:''' | ||
| + | | <math>\phi^{(n)}_{i+1} \leftarrow \phi_{B} (\mathbf{N}^{(n-1)}_{i+1})</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |xx | ||
| + | |x | ||
| + | | | ||
| + | | | ||
| + | |} | ||
== Usage == | == Usage == | ||
Revision as of 09:12, 29 September 2017
The Stochastic Implicit Euler (SIE) burnup scheme is an alternative burnup scheme that can be used if the traditional predictor-corrector burnup schemes in Serpent exhibit unstable behavior.
Background
The theoretical background of the SIE scheme is described in [1]
Input
The SIE burnup scheme can be chosen with the set sie input card. The number of iterations for each burnup steps can be specified.
Some additional input options that many times are combined with the set sie card are set fsp for passing the fission source from the end of previous neutron transport solution to the beginning of the next one, and set cpop to use an alternate (typically lower) neutron population for the SIE iteration (compared to the neutron population used on the initial predictor step.
Implementation
For burnup calculations, Serpent needs to evaluate the one group flux 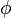 for each depletion region and one group fission/transmutation cross sections
for each depletion region and one group fission/transmutation cross sections 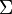 for each fission/transmutation reaction of each nuclide.
for each fission/transmutation reaction of each nuclide.
These can then be used for calculating the reaction rates required for assembling the burnup matrix 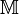 . The following algorithmic description uses
. The following algorithmic description uses 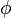 to refer to both the one group burn flux and the one group cross sections.
to refer to both the one group burn flux and the one group cross sections.
| 1: | input: 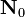
|
Start from initial nuclide concentrations. | ||
| 2: | 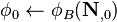
|
Calculate 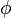 using initial nuclide concentrations. using initial nuclide concentrations.
| ||
| 3: | for 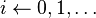 do do
|
Loop over burnup points. | ||
| 4: | ![\mathbf{N}_{i+1}^{(0)} \leftarrow \exp \left[ \mathbb{M}(\phi_{i}) \Delta t\right] \mathbf{N}_{i}](/mediawiki/images/math/2/5/3/25389338a07bf23fb750b5ab78ff2720.png)
|
Burn forward (predictor) using previously obtained BOS 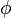 . .
| ||
| 5: | for 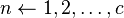 do do
|
Loop over iterations for current burnup point. | ||
| 6: | 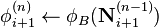
|
|||
| xx | x | |||
Usage
Noteworthy things
- No neutron transport solution is actually calculated using the final concentrations for a certain point.
References
- ^ Dufek, J., Kotlyar, D. and Shwageraus, E. "The stochastic implicit Euler method – A stable coupling scheme for Monte Carlo burnup calculations", Ann. Nucl. Energy, 60 (2013) 295-300