SuperFINIX theory manual
Field transfers from SuperFINIX meshes to FINIX meshes
Power from SuperFINIX to FINIX
SuperFINIX receives power densities in blocks that have to be discretized in the radial nodes of FINIX. This discretization is based on assumption that the number of axial elements remains unchanged before and after the discretization. Therefore the discretization is only performed in the radial dimension. The main solvers in FINIX assume linear scaling of power density (and most other variables) between two nodal points. Because of this assumption, the power densities in nodes have to adjusted when integrating over a volume element that is spanned by two radial nodes in different power density blocks. This conserves the total power over the volumes of single elements as well as the whole fuel rod volume. As such, the following condition has to hold true for the scenario of Figure 1:
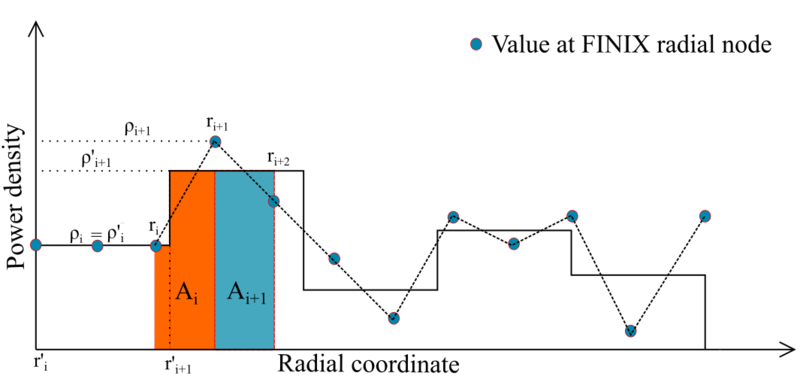
-
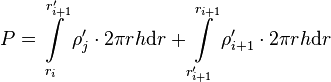
(1)
and
-
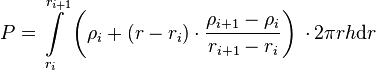
(2)
where:
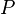
The total power in a volume element, 
Radial coordinate of a radial node in FINIX, 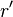
Radial coordinate at the beginning of a power density block in SuperFINIX, 
Power density of a radial node in FINIX, 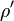
Power density of a block in SuperFINIX, 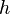
Axial length of the volume element.
Equation 2 can be solved for 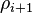 to obtain the power densities at all radial nodes as:
to obtain the power densities at all radial nodes as:
-
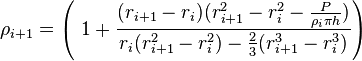
(3)
here P is the total power of the element which can be solved from Equation 1 and the power density of the first node  is always equal to the power density of the first block. For situations in which adjacent FINIX radial nodes are separated by several SuperFINIX blocks, the calculation of total power P can be generalized as:
is always equal to the power density of the first block. For situations in which adjacent FINIX radial nodes are separated by several SuperFINIX blocks, the calculation of total power P can be generalized as:
-
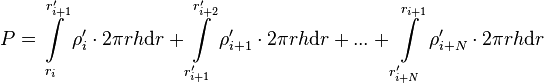
(4)