Kharon theory manual
Conservation of Mass
Steady one-dimensional conservation of mass (of phase q) is given through the following relation
-
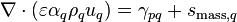
(1)
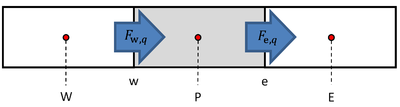
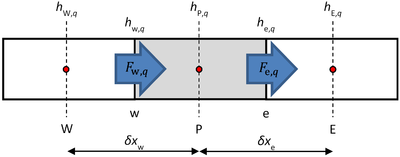
Equation 1 is discretized for an interior cell, shown in Figure 1, by volume integration over cell P.
-
![\Leftrightarrow \iiint\limits_V [\nabla\cdot(\varepsilon \alpha_q \rho_q u_q)]\, dV = \iiint\limits_V (\gamma_{pq} + s_{\text{mass},q})\, dV](/kraken/images/math/3/1/e/31e2c304fe57f1baacc0de339b9e12c9.png)
(2)
The divergence term on the left-hand side of the equation is transformed into a surface integral over the cell faces using the divergence theorem.
-
![\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset [(\varepsilon \alpha_q \rho_q u_q)\cdot n]\, dA = \iiint\limits_V (\gamma_{pq} + s_{\text{mass},q})\, dV](/kraken/images/math/2/0/b/20b292d715b6ac3b0160f63a290ba14e.png)
(3)
Throughout this document upwind discretization is used to evaluate the face mass flow rates, even though any discretization scheme could be chosen. The final discretized form reduces to
-
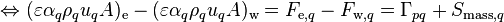
(4)
where:
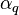
volume fraction of phase q [-], 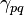
volumetric mass transfer rate from phase p to q [kg/m3s], 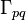
mass transfer rate from phase p to q [kg/s], 
porosity, fluid fraction of cell volume [-], 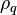
density of phase q [kg/m3], 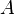
face area [m2], 
face mass flow rate [kg/s], 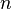
face normal pointing out of the cell (1 for east face, -1 for west face), 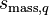
volumetric mass source to phase q [kg/m3s], 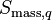
mass source to phase q [kg/s], 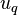
velocity of phase q [m/s], subscript e east face (the face in the negative x-direction), subscript w west face (the face in the positive x-direction), subscript q current phase for which the equation is written (1 = primary, 2 = secondary), subscript p the other phase (p = 2 for q = 1 and p = 1 for q = 2), subscript pq indicates exchange between phases (e.g. 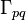 mass transfer from phase p to q).
mass transfer from phase p to q).
Conservation of Momentum
Steady one-dimensional conservation of momentum (of phase q) is solved from the following relation
-
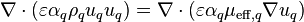
(5)
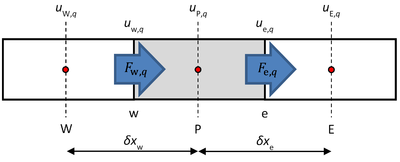
Equation 5 is discretized for an interior cell, shown in Figure 2, by volume integration over cell P. The diffusion term has been moved to the left-hand side, since it will be developed together with the divergence of momentum.
-
![\Leftrightarrow \iiint\limits_V [\nabla\cdot(\varepsilon \alpha_q \rho_q u_q u_q) - \nabla\cdot(\varepsilon \alpha_q \mu_{\text{eff},q} \nabla u_q)]\, dV = \iiint\limits_V [\text{max}(\gamma_{pq},0)u_p - \text{max}(-\gamma_{pq},0)u_q]\, dV](/kraken/images/math/6/e/c/6ec72027cf12525c153f8a65271118f4.png)
(6)
As with the conservation of mass equation above, the divergence terms on the left-hand side of the equation are transformed into surface integrals over the cell faces using the divergence theorem.
-
![\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset [(\varepsilon \alpha_q \rho_q u_q u_q)\cdot n - (\varepsilon \alpha_q \mu_{\text{eff},q} \frac{\Delta u_q}{\delta x})\cdot n]\, dA = [\text{max}(\Gamma_{pq},0)u_p - \text{max}(-\Gamma_{pq},0)u_q]](/kraken/images/math/0/e/9/0e9c661b0f8bc98b73d33fe1a89d0bcb.png)
(7)
Developing the left-hand side terms first
-
![\iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset [(\varepsilon \alpha_q \rho_q u_q u_q)\cdot n - (\varepsilon \alpha_q \mu_{\text{eff},q} \frac{\Delta u_q}{\delta x})\cdot n]\, dA](/kraken/images/math/f/2/8/f2878f17952e19703b9615e3a2fee471.png)
(8)
Adopting upwind discretization for the momentum fluxes on the cell faces
-
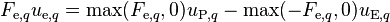
(9)
-
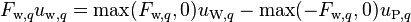
(10)
and rearranging terms
-
![\iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset [(\varepsilon \alpha_q \rho_q u_q u_q)\cdot n - (\varepsilon \alpha_q \mu_{\text{eff},q} \frac{\Delta u_q}{\delta x})\cdot n]\, dA](/kraken/images/math/f/2/8/f2878f17952e19703b9615e3a2fee471.png)
(11)
Denoting 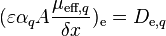 and
and  and modifying the central coefficient slightly, since
and modifying the central coefficient slightly, since 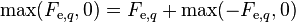 and
and  , Equation 11 reduces to
, Equation 11 reduces to
-
![\iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset [(\varepsilon \alpha_q \rho_q u_q u_q)\cdot n - (\varepsilon \alpha_q \mu_{\text{eff},q} \frac{\Delta u_q}{\delta x})\cdot n]\, dA](/kraken/images/math/f/2/8/f2878f17952e19703b9615e3a2fee471.png)
(12)
Identifying the coefficients of neighboring velocities
-

(13)
-
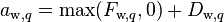
(14)
leads to a general form
-
![\iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset [(\varepsilon \alpha_q \rho_q u_q u_q)\cdot n - (\varepsilon \alpha_q \mu_{\text{eff},q} \frac{\Delta u_q}{\delta x})\cdot n]\, dA](/kraken/images/math/f/2/8/f2878f17952e19703b9615e3a2fee471.png)
(15)
Conservation of Total Enthalpy
![+ [\text{max}(\gamma_{pq},0)u_p - \text{max}(-\gamma_{pq},0)u_q] - \varepsilon \alpha_q \nabla p + \varepsilon \alpha_q \rho_q g](/kraken/images/math/0/a/2/0a2a75fc78a0f35645e886418bdc4026.png)
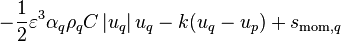
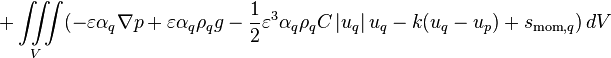
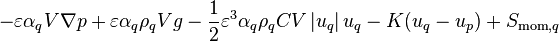
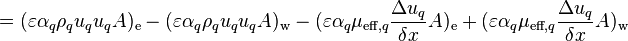
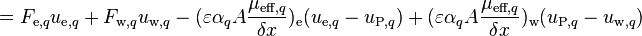
![=[\text{max}(F_{\text{e},q},0) + \text{max}(-F_{\text{w},q},0) + (\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x})_{\text{e}} + (\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x})_{\text{w}}]u_{\text{P},q}](/kraken/images/math/8/4/6/8467e816d3f2fb23f04821cb4926e66c.png)
![-[\text{max}(-F_{\text{e},q},0) + (\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x})_{\text{e}}]u_{\text{E},q}](/kraken/images/math/4/a/0/4a0bf6a82efcd98195a69f89732b4e32.png)
![-[\text{max}(F_{\text{w},q},0) + (\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x})_{\text{w}}]u_{\text{W},q}](/kraken/images/math/c/2/8/c28da5213c92f3f04357691fae2d3cb8.png)
![= [\text{max}(-F_{\text{e},q},0) + D_{\text{e},q} + \text{max}(F_{\text{w},q},0) + D_{\text{w},q} + (F_{\text{e},q} - F_{\text{w},q})]u_{\text{P},q}](/kraken/images/math/8/e/c/8ece301a15289685cc994bf8acfec9c1.png)
![-[\text{max}(-F_{\text{e},q},0) + D_{\text{e},q}]u_{\text{E},q} - [\text{max}(F_{\text{w},q},0) + D_{\text{w},q}]u_{\text{W},q}](/kraken/images/math/0/c/5/0c5340ecf0ea4e86e814c53671d6ec89.png)
![= [a_{\text{e},q} + a_{\text{w},q} + (F_{\text{e},q} - F_{\text{w},q})]u_{\text{P},q} - a_{\text{e},q}u_{\text{E},q} - - a_{\text{w},q}u_{\text{W},q}](/kraken/images/math/7/e/1/7e15b0432df8e1fe13934a4c5d9b1c02.png)