Difference between revisions of "SuperFINIX theory manual"

From Kraken Wiki
Jump to: navigation, search
(→‎Temperature from FINIX to SuperFINIX)
(→‎Temperature from FINIX to SuperFINIX)
Line 121: Line 121:
 
</equation>
 
</equation>
  
−
<math> = \frac{\left( T'_{i} -  (T_{i} - T'_{i}) \frac{r_i}{r'_i - r'_{i}}\right)\ </math>
+
<math> = \left( T'_{i} -  (T_{i} - T'_{i}) \frac{r_i}{r'_i - r'_{i}}\right)\ </math>
  
  

Revision as of 13:53, 17 July 2019


Field transfers from SuperFINIX meshes to FINIX meshes

Power from SuperFINIX to FINIX

SuperFINIX receives power densities in blocks that have to be discretized in the radial nodes of FINIX. This discretization is based on assumption that the number of axial elements remains unchanged before and after the discretization. Therefore the discretization is only performed in the radial dimension. The main solvers in FINIX assume linear scaling of power density (and most other variables) between two nodal points. Because of this assumption, the power densities in nodes have to adjusted when integrating over a volume element that is spanned by two radial nodes in different power density blocks. This conserves the total power over the volumes of single elements as well as the whole fuel rod volume. As such, the following condition has to hold true for the scenario of Figure 2:

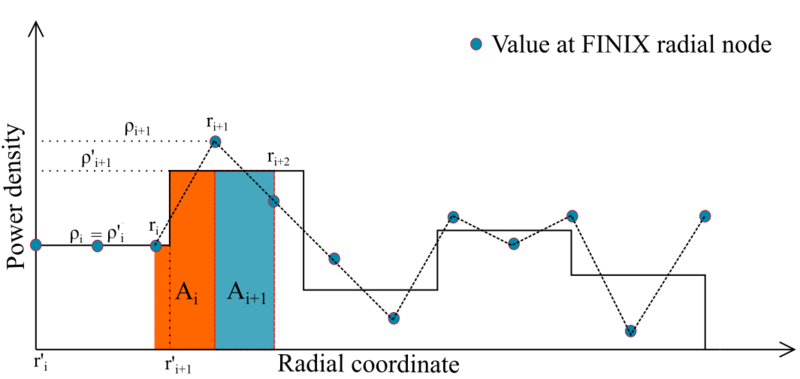
Figure 2: Discretization of a power field in SuperFINIX-FINIX coupling.

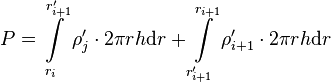
P = \int\limits_{r_i}^{r'_{i+1}} \rho'_j \cdot 2\pi r h \text{d}r + \int\limits_{r'_{i+1}}^{r_{i+1}} \rho'_{i+1} \cdot 2\pi r h \text{d}r

 

 

 

 

(5)

and

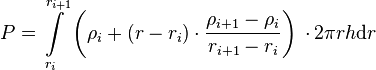
P = \int\limits_{r_i}^{r_{i+1}} \left(\rho_i + (r - r_i) \cdot \frac{\rho_{i+1} - \rho_i}{r_{i+1} - r_{i}} \right)\, \cdot 2\pi r h \text{d}r

 

 

 

 

(6)

where:

P The total power in a volume element,
r Radial coordinate of a radial node in FINIX,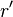
r' Radial coordinate at the beginning of a power density block in SuperFINIX,
\rho Power density of a radial node in FINIX,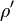
\rho' Power density of a block in SuperFINIX,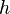
h Axial length of the volume element.

Equation 6 can be solved for 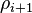\rho_{i+1} to obtain the power densities at all radial nodes as:

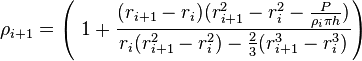
\rho_{i+1} = \left(\ 1 + \frac{(r_{i+1} - r_i)(r_{i+1}^2 - r_i^2 - \frac{P}{\rho_i \pi h})}{r_i(r_{i+1}^2 - r_i^2)-\frac{2}{3}(r_{i+1}^3 - r_i^3)} \right)\

 

 

 

 

(7)

here P is the total power of the element which can be solved from Equation 5 and the power density of the first node \rho_1 is always equal to the power density of the first block. For situations in which adjacent FINIX radial nodes are separated by several SuperFINIX blocks, the calculation of total power P can be generalized as:

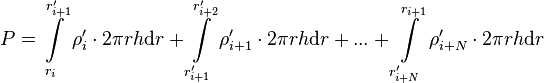
P = \int\limits_{r_i}^{r'_{i+1}} \rho'_i \cdot 2\pi r h \text{d}r + \int\limits_{r'_{i+1}}^{r'_{i+2}} \rho'_{i+1} \cdot 2\pi r h \text{d}r + ... + \int\limits_{r'_{i+N}}^{r_{i+1}} \rho'_{i+N} \cdot 2\pi r h \text{d}r

 

 

 

 

(8)

Field transfers from SuperFINIX meshes to FINIX meshes

Power from SuperFINIX to FINIX

SuperFINIX receives power densities in blocks that have to be discretized in the radial nodes of FINIX. This discretization is based on assumption that the number of axial elements remains unchanged before and after the discretization. Therefore the discretization is only performed in the radial dimension. The main solvers in FINIX assume linear scaling of power density (and most other variables) between two nodal points. Because of this assumption, the power densities in nodes have to adjusted when integrating over a volume element that is spanned by two radial nodes in different power density blocks. This conserves the total power over the volumes of single elements as well as the whole fuel rod volume. As such, the following condition has to hold true for the scenario of Figure 2:

Figure 2: Discretization of a power field in SuperFINIX-FINIX coupling.

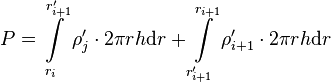
P = \int\limits_{r_i}^{r'_{i+1}} \rho'_j \cdot 2\pi r h \text{d}r + \int\limits_{r'_{i+1}}^{r_{i+1}} \rho'_{i+1} \cdot 2\pi r h \text{d}r

 

 

 

 

(5)

and

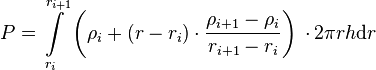
P = \int\limits_{r_i}^{r_{i+1}} \left(\rho_i + (r - r_i) \cdot \frac{\rho_{i+1} - \rho_i}{r_{i+1} - r_{i}} \right)\, \cdot 2\pi r h \text{d}r

 

 

 

 

(6)

where:

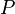
P The total power in a volume element,
r Radial coordinate of a radial node in FINIX,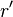
r' Radial coordinate at the beginning of a power density block in SuperFINIX,
\rho Power density of a radial node in FINIX,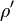
\rho' Power density of a block in SuperFINIX,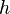
h Axial length of the volume element.

Equation 6 can be solved for 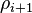\rho_{i+1} to obtain the power densities at all radial nodes as:

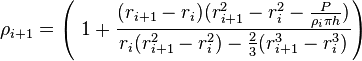
\rho_{i+1} = \left(\ 1 + \frac{(r_{i+1} - r_i)(r_{i+1}^2 - r_i^2 - \frac{P}{\rho_i \pi h})}{r_i(r_{i+1}^2 - r_i^2)-\frac{2}{3}(r_{i+1}^3 - r_i^3)} \right)\

 

 

 

 

(7)

here P is the total power of the element which can be solved from Equation 5 and the power density of the first node \rho_1 is always equal to the power density of the first block. For situations in which adjacent FINIX radial nodes are separated by several SuperFINIX blocks, the calculation of total power P can be generalized as:

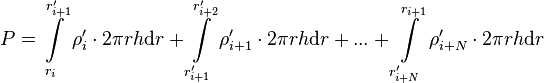
P = \int\limits_{r_i}^{r'_{i+1}} \rho'_i \cdot 2\pi r h \text{d}r + \int\limits_{r'_{i+1}}^{r'_{i+2}} \rho'_{i+1} \cdot 2\pi r h \text{d}r + ... + \int\limits_{r'_{i+N}}^{r_{i+1}} \rho'_{i+N} \cdot 2\pi r h \text{d}r

 

 

 

 

(8)

Temperature from FINIX to SuperFINIX

FINIX calculates the fuel temperatures at nodal points, from which temperatures of the SuperFINIX blocks have to be calculated. First the temperatures have to be linearly interpolated to calculate the temperatures at the beginning of each block:

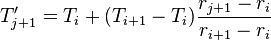
T'_{j+1} = T_i + (T_{i+1} - T_i) \frac{r_{j+1} - r_{i}}{r_{i+1}-r_i}

 

 

 

 

(9)

Once the interpolated temperatures 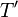T' are known, the average temperature of each block 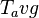T_avg can be calculated by integrating the linearly scaling temperature over the volume of the block and then dividing it with the total volume. For a block of scenario Figure 3 containing two radial nodes this is done as:

T_{avg} = \frac{\int\limits_{r'_i}^{r_{i}} \left(T'_i + (r - r'_i) \cdot \frac{T_{i} - T'_i}{r_{i} - r'_{i}} \right)\, \cdot 2\pi r h \text{d}r + \int\limits_{r_i}^{r'_{i+1}} \left(T_i + (r - r_i) \cdot \frac{T'_{i+1} - T_i}{r'_{i+1} - r_{i}} \right)\, \cdot 2\pi r h \text{d}r}{V_j} = \frac{\int\limits_{r'_{i}}^{r_{i}} \left(T'_i + (r - r'_i) \cdot \frac{T_{i} - T'_i}{r_{i} - r'_{i}} \right)\, \cdot 2\pi r h \text{d}r + \int\limits_{r_i}^{r'_{i+1}} \left(T_i + (r - r_i) \cdot \frac{T'_{i+1} - T_i}{r'_{i+1} - r_{i}} \right)\, \cdot 2\pi r h \text{d}r}{\pi ({r'}_{i+1}^2 - {r'}_{i}^2) h}

 

 

 

 

(11)

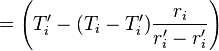
= \left( T'_{i} - (T_{i} - T'_{i}) \frac{r_i}{r'_i - r'_{i}}\right)\


Figure 3: Calculation of a temperature field in FINIX-SuperFINIX coupling.

For scenarios in which a SuperFINIX block contains several FINIX radial nodes, the formula can be generalized as:

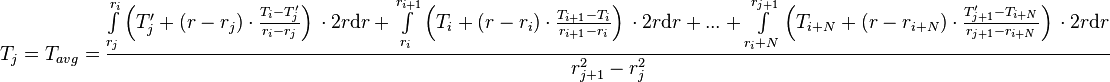
T_{j} = T_{avg} = \frac{\int\limits_{r_j}^{r_{i}} \left(T'_j + (r - r_j) \cdot \frac{T_{i} - T'_j}{r_{i} - r_{j}} \right)\, \cdot 2 r\text{d}r + \int\limits_{r_i}^{r_{i+1}} \left(T_i + (r - r_i) \cdot \frac{T_{i+1} - T_i}{r_{i+1} - r_{i}} \right)\, \cdot 2 r \text{d}r + ... + \int\limits_{r_i+N}^{r_{j+1}} \left(T_{i+N} + (r - r_{i+N}) \cdot \frac{T'_{j+1} - T_{i+N}}{r_{j+1} - r_{i+N}} \right)\, \cdot 2 r \text{d}r}{r_{j+1}^2 - r_{j}^2}

 

 

 

 

(11)

Retrieved from "https://serpent.vtt.fi/kraken/index.php?title=SuperFINIX_theory_manual&oldid=993"