Difference between revisions of "Kharon theory manual"
Ville Hovi (talk | contribs) (→Conservation of Total Enthalpy) |
Ville Hovi (talk | contribs) |
||
| Line 136: | Line 136: | ||
::::::::<math> -\left[\text{max}\left(F_{\text{w},q},0\right) + \left(\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x}\right)_{\text{w}}\right]u_{\text{W},q} </math> | ::::::::<math> -\left[\text{max}\left(F_{\text{w},q},0\right) + \left(\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x}\right)_{\text{w}}\right]u_{\text{W},q} </math> | ||
</equation> | </equation> | ||
| − | |||
Denoting <math>\left(\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x}\right)_{\text{e}} = D_{\text{e},q}</math> and <math>\left(\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x}\right)_{\text{w}} = D_{\text{w},q}</math> and modifying the central coefficient slightly, since <math>\text{max}\left(F_{\text{e},q},0\right) = F_{\text{e},q} + \text{max}\left(-F_{\text{e},q},0\right)</math> and <math>\text{max}\left(-F_{\text{w},q},0\right) = -F_{\text{w},q} + \text{max}\left(F_{\text{w},q},0\right)</math>, <xr id="eqn:MomentumConservation5"/> reduces to | Denoting <math>\left(\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x}\right)_{\text{e}} = D_{\text{e},q}</math> and <math>\left(\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x}\right)_{\text{w}} = D_{\text{w},q}</math> and modifying the central coefficient slightly, since <math>\text{max}\left(F_{\text{e},q},0\right) = F_{\text{e},q} + \text{max}\left(-F_{\text{e},q},0\right)</math> and <math>\text{max}\left(-F_{\text{w},q},0\right) = -F_{\text{w},q} + \text{max}\left(F_{\text{w},q},0\right)</math>, <xr id="eqn:MomentumConservation5"/> reduces to | ||
| − | |||
<equation id="eqn:MomentumConservation6"> | <equation id="eqn:MomentumConservation6"> | ||
| Line 146: | Line 144: | ||
::::::::<math>-\left[\text{max}\left(-F_{\text{e},q},0\right) + D_{\text{e},q}\right]u_{\text{E},q} - \left[\text{max}\left(F_{\text{w},q},0\right) + D_{\text{w},q}\right]u_{\text{W},q}</math> | ::::::::<math>-\left[\text{max}\left(-F_{\text{e},q},0\right) + D_{\text{e},q}\right]u_{\text{E},q} - \left[\text{max}\left(F_{\text{w},q},0\right) + D_{\text{w},q}\right]u_{\text{W},q}</math> | ||
</equation> | </equation> | ||
| − | |||
Identifying the coefficients of neighboring velocities | Identifying the coefficients of neighboring velocities | ||
| Line 424: | Line 421: | ||
<equation id="eqn:TotalEnthalpyConservation3"> | <equation id="eqn:TotalEnthalpyConservation3"> | ||
{{NumBlk|:|<math>\Rightarrow\nabla\cdot\left(\varepsilon \alpha_q \rho_q h_q u_q\right) - \nabla\cdot\left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \nabla h_q \right)</math>|<xr id="eqn:TotalEnthalpyConservation3" nolink />}} | {{NumBlk|:|<math>\Rightarrow\nabla\cdot\left(\varepsilon \alpha_q \rho_q h_q u_q\right) - \nabla\cdot\left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \nabla h_q \right)</math>|<xr id="eqn:TotalEnthalpyConservation3" nolink />}} | ||
| − | ::::<math>= \left[\text{max}\left(\gamma_{pq},0\right) \left(h_{\text{P,sat,}q} + \tfrac{1}{2} \left| u_p \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right) - \text{max}\left(-\gamma_{pq},0\right) \left(h_{\text{P,}q} + \tfrac{1}{2} \left| u_q \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}} | + | ::::<math>= \left[\text{max}\left(\gamma_{pq},0\right) \left(h_{\text{P,sat,}q} + \tfrac{1}{2} \left| u_p \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right) - \text{max}\left(-\gamma_{pq},0\right) \left(h_{\text{P,}q} + \tfrac{1}{2} \left| u_q \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right)\right]</math> |
| − | \right)\right]</math> | ||
::::<math> -\nabla\cdot\left(\tfrac{1}{2}\varepsilon \alpha_q \rho_q \left| u_q \right|^2 u_q\right) | ::::<math> -\nabla\cdot\left(\tfrac{1}{2}\varepsilon \alpha_q \rho_q \left| u_q \right|^2 u_q\right) | ||
+\nabla\cdot\left(\varepsilon \alpha_q \rho_q \left( \mathbf{g} \cdot \mathbf{r} \right)u_q\right) | +\nabla\cdot\left(\varepsilon \alpha_q \rho_q \left( \mathbf{g} \cdot \mathbf{r} \right)u_q\right) | ||
| Line 434: | Line 430: | ||
<equation id="eqn:TotalEnthalpyConservation4"> | <equation id="eqn:TotalEnthalpyConservation4"> | ||
| − | {{NumBlk|:|<math>\Leftrightarrow\nabla\cdot\left(\varepsilon \alpha_q \rho_q h_q u_q\right) - \nabla\cdot\left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \nabla h_q \right)</math>|<xr id="eqn:TotalEnthalpyConservation4" nolink />}} | + | {{NumBlk|:|<math>\Leftrightarrow \iiint\limits_V \left[\nabla\cdot\left(\varepsilon \alpha_q \rho_q h_q u_q\right) - \nabla\cdot\left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \nabla h_q \right)\right]\, dV </math>|<xr id="eqn:TotalEnthalpyConservation4" nolink />}} |
| − | ::::<math>= \left[\text{max}\left(\gamma_{pq},0\right) \left(h_{\text{P,sat,}q} + \tfrac{1}{2} \left| u_p \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right) - \text{max}\left(-\gamma_{pq},0\right) \left(h_{\text{P,}q} + \tfrac{1}{2} \left| u_q \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}} | + | ::::<math>= \iiint\limits_V \Big\{ \left[\text{max}\left(\gamma_{pq},0\right) \left(h_{\text{P,sat,}q} + \tfrac{1}{2} \left| u_p \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right) - \text{max}\left(-\gamma_{pq},0\right) \left(h_{\text{P,}q} + \tfrac{1}{2} \left| u_q \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right)\right]</math> |
| − | \right)\right]</math> | + | ::::<math> -\nabla\cdot\left(\tfrac{1}{2}\varepsilon \alpha_q \rho_q \left| u_q \right|^2 u_q\right) |
| + | +\nabla\cdot\left(\varepsilon \alpha_q \rho_q \left( \mathbf{g} \cdot \mathbf{r} \right)u_q\right) | ||
| + | -\nabla\cdot\left(\varepsilon \alpha_q \mathbf{q} \right) + \nabla\cdot\left(\varepsilon \alpha_q \boldsymbol{\tau} \cdot \mathbf{u}_q \right) + s_{h,q} \Big\}\, dV </math> | ||
| + | </equation> | ||
| + | |||
| + | As with the conservation of mass and momentum above, the divergence terms on the left-hand side of the equation are transformed into surface integrals over the cell faces using the divergence theorem. | ||
| + | |||
| + | <equation id="eqn:TotalEnthalpyConservation5"> | ||
| + | {{NumBlk|:|<math>\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q h_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \frac{\Delta h_q}{\delta x}\right)\cdot n\right]\, dA</math>|<xr id="eqn:TotalEnthalpyConservation5" nolink />}} | ||
| + | ::::<math>= \iiint\limits_V \Big\{ \left[\text{max}\left(\gamma_{pq},0\right) \left(h_{\text{P,sat,}q} + \tfrac{1}{2} \left| u_p \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right) - \text{max}\left(-\gamma_{pq},0\right) \left(h_{\text{P,}q} + \tfrac{1}{2} \left| u_q \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right)\right]</math> | ||
| + | ::::<math> -\nabla\cdot\left(\tfrac{1}{2}\varepsilon \alpha_q \rho_q \left| u_q \right|^2 u_q\right) | ||
| + | +\nabla\cdot\left(\varepsilon \alpha_q \rho_q \left( \mathbf{g} \cdot \mathbf{r} \right)u_q\right) | ||
| + | -\nabla\cdot\left(\varepsilon \alpha_q \mathbf{q} \right) + \nabla\cdot\left(\varepsilon \alpha_q \boldsymbol{\tau} \cdot \mathbf{u}_q \right) + s_{h,q} \Big\}\, dV </math> | ||
| + | </equation> | ||
| + | |||
| + | Developing the left-hand side first. | ||
| + | |||
| + | <equation id="eqn:TotalEnthalpyConservation6"> | ||
| + | {{NumBlk|:|<math>\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q h_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \frac{\Delta h_q}{\delta x}\right)\cdot n\right]\, dA</math>|<xr id="eqn:TotalEnthalpyConservation6" nolink />}} | ||
| + | ::::<math> = \left(\varepsilon \alpha_q \rho_q h_q u_q A\right)_{\text{e}} - \left(\varepsilon \alpha_q \rho_q h_q u_q A\right)_{\text{w}} - \left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \frac{\Delta h_q}{\delta x} A\right)_{\text{e}} + \left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \frac{\Delta h_q}{\delta x} A\right)_{\text{w}} </math> | ||
| + | ::::<math> = F_{\text{e},q} h_{\text{e},q} + F_{\text{w},q} h_{\text{w},q} - \left(\varepsilon \alpha_q A \frac{\lambda_{\text{eff},q}}{c_{p,q}\delta x}\right)_{\text{e}} \left(h_{\text{E},q} - h_{\text{P},q}\right) + \left(\varepsilon \alpha_q A \frac{\lambda_{\text{eff},q}}{c_{p,q}\delta x}\right)_{\text{w}} \left(h_{\text{P},q} - h_{\text{W},q}\right) </math> | ||
| + | </equation> | ||
| + | |||
| + | Adopting upwind discretization for the enthalpy fluxes on the cell faces | ||
| + | |||
| + | <equation id="eqn:UpwindEnthalpyFluxes"> | ||
| + | {{NumBlk|:|<math> | ||
| + | \begin{align} | ||
| + | & F_{\text{e},q} h_{\text{e},q} = \text{max}\left(F_{\text{e},q},0\right) h_{\text{P},q} - \text{max}\left(-F_{\text{e},q},0\right) h_{\text{E},q}\\ | ||
| + | & F_{\text{w},q} h_{\text{w},q} = \text{max}\left(F_{\text{w},q},0\right) h_{\text{W},q} - \text{max}\left(-F_{\text{w},q},0\right) h_{\text{P},q} | ||
| + | \end{align} | ||
| + | </math>|<xr id="eqn:UpwindEnthalpyFluxes" nolink />}} | ||
| + | </equation> | ||
| + | |||
| + | and rearranging terms | ||
| + | |||
| + | <equation id="eqn:TotalEnthalpyConservation7"> | ||
| + | {{NumBlk|:|<math>\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q h_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \frac{\Delta h_q}{\delta x}\right)\cdot n\right]\, dA</math>|<xr id="eqn:TotalEnthalpyConservation7" nolink />}} | ||
| + | ::::<math> = \left[ \text{max}\left(F_{\text{e},q},0\right) + \text{max}\left(-F_{\text{w},q},0\right) + \left(\varepsilon \alpha_q A \frac{\lambda_{\text{eff},q}}{c_{p,q}\delta x}\right)_{\text{e}} + \left(\varepsilon \alpha_q A \frac{\lambda_{\text{eff},q}}{c_{p,q}\delta x}\right)_{\text{w}} \right] h_{\text{P},q}</math> | ||
| + | ::::<math> - \left[ \text{max}\left(-F_{\text{e},q},0\right) + \left(\varepsilon \alpha_q A \frac{\lambda_{\text{eff},q}}{c_{p,q}\delta x}\right)_{\text{e}} \right] h_{\text{E},q} - \left[ \text{max}\left(F_{\text{w},q},0\right) + \left(\varepsilon \alpha_q A \frac{\lambda_{\text{eff},q}}{c_{p,q}\delta x}\right)_{\text{w}} \right] h_{\text{W},q}</math> | ||
| + | </equation> | ||
| + | |||
| + | |||
| + | Denoting <math>\left(\varepsilon \alpha_q A \frac{\lambda_{\text{eff},q}}{c_{p,q}\delta x}\right)_{\text{e}} = D_{\text{e},q}</math> and <math>\left(\varepsilon \alpha_q A \frac{\lambda_{\text{eff},q}}{c_{p,q}\delta x}\right)_{\text{w}} = D_{\text{w},q}</math> and modifying the central coefficient slightly, since <math>\text{max}\left(F_{\text{e},q},0\right) = F_{\text{e},q} + \text{max}\left(-F_{\text{e},q},0\right)</math> and <math>\text{max}\left(-F_{\text{w},q},0\right) = -F_{\text{w},q} + \text{max}\left(F_{\text{w},q},0\right)</math>, <xr id="eqn:TotalEnthalpyConservation7"/> reduces to | ||
| + | |||
| + | <equation id="eqn:TotalEnthalpyConservation8"> | ||
| + | {{NumBlk|:|<math>\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q h_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \frac{\Delta h_q}{\delta x}\right)\cdot n\right]\, dA</math>|<xr id="eqn:TotalEnthalpyConservation8" nolink />}} | ||
| + | ::::<math> = \left[ \text{max}\left(-F_{\text{e},q},0\right) + D_{\text{e},q} + \text{max}\left(F_{\text{w},q},0\right) + D_{\text{w},q} + \left( F_{\text{e},q} - F_{\text{w},q} \right) \right] h_{\text{P},q} </math> | ||
| + | ::::<math> - \left[ \text{max}\left(-F_{\text{e},q},0\right) + D_{\text{e},q} \right] h_{\text{E},q} | ||
| + | - \left[ \text{max}\left(F_{\text{w},q},0\right) + D_{\text{w},q} \right] h_{\text{W},q} </math> | ||
| + | </equation> | ||
| + | |||
| + | |||
| + | Identifying the coefficients of neighboring velocities as | ||
| + | |||
| + | <equation id="eqn:EnthalpyNeighborCoefficients"> | ||
| + | {{NumBlk|:|<math> | ||
| + | \begin{align} | ||
| + | & a_{\text{e},q} = \text{max}\left(-F_{\text{e},q},0\right) + D_{\text{e},q}\\ | ||
| + | & a_{\text{w},q} = \text{max}\left(F_{\text{w},q},0\right) + D_{\text{w},q} | ||
| + | \end{align} | ||
| + | </math>|<xr id="eqn:EnthalpyNeighborCoefficients" nolink />}} | ||
| + | </equation> | ||
| + | |||
| + | leads to a general form | ||
| + | |||
| + | <equation id="eqn:TotalEnthalpyConservation9"> | ||
| + | {{NumBlk|:|<math>\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q h_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \frac{\Delta h_q}{\delta x}\right)\cdot n\right]\, dA</math>|<xr id="eqn:TotalEnthalpyConservation9" nolink />}} | ||
| + | ::::<math> = \left[ a_{\text{e},q} + a_{\text{w},q} + \left( F_{\text{e},q} - F_{\text{w},q} \right) \right] h_{\text{P},q} - a_{\text{e},q} h_{\text{E},q} - a_{\text{w},q} h_{\text{W},q}</math> | ||
| + | </equation> | ||
| + | |||
| + | Substituting the results of <xr id="eqn:TotalEnthalpyConservation9"/> into <xr id="eqn:TotalEnthalpyConservation5"/> and continuing with the development | ||
| + | |||
| + | <equation id="eqn:TotalEnthalpyConservation10"> | ||
| + | {{NumBlk|:|<math>\Rightarrow \left[ a_{\text{e},q} + a_{\text{w},q} + \left( F_{\text{e},q} - F_{\text{w},q} \right) \right] h_{\text{P},q} - a_{\text{e},q} h_{\text{E},q} - a_{\text{w},q} h_{\text{W},q}\, dA</math>|<xr id="eqn:TotalEnthalpyConservation10" nolink />}} | ||
| + | ::::<math>= \iiint\limits_V \Big\{ \left[\text{max}\left(\gamma_{pq},0\right) \left(h_{\text{P,sat,}q} + \tfrac{1}{2} \left| u_p \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right) - \text{max}\left(-\gamma_{pq},0\right) \left(h_{\text{P,}q} + \tfrac{1}{2} \left| u_q \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right)\right]</math> | ||
::::<math> -\nabla\cdot\left(\tfrac{1}{2}\varepsilon \alpha_q \rho_q \left| u_q \right|^2 u_q\right) | ::::<math> -\nabla\cdot\left(\tfrac{1}{2}\varepsilon \alpha_q \rho_q \left| u_q \right|^2 u_q\right) | ||
+\nabla\cdot\left(\varepsilon \alpha_q \rho_q \left( \mathbf{g} \cdot \mathbf{r} \right)u_q\right) | +\nabla\cdot\left(\varepsilon \alpha_q \rho_q \left( \mathbf{g} \cdot \mathbf{r} \right)u_q\right) | ||
| − | -\nabla\cdot\left(\varepsilon \alpha_q \mathbf{q} \right) + \nabla\cdot\left(\varepsilon \alpha_q \boldsymbol{\tau} \cdot \mathbf{u}_q \right) + s_{h,q}</math> | + | -\nabla\cdot\left(\varepsilon \alpha_q \mathbf{q} \right) + \nabla\cdot\left(\varepsilon \alpha_q \boldsymbol{\tau} \cdot \mathbf{u}_q \right) + s_{h,q} \Big\}\, dV </math> |
| + | </equation> | ||
| + | |||
| + | Integrating the right-hand side term by term. The phase change term reduces to | ||
| + | |||
| + | <equation id="eqn:TotalEnthalpyConservation10"> | ||
| + | {{NumBlk|:|<math>\iiint\limits_V \left[\text{max}\left(\gamma_{pq},0\right) \left(h_{\text{P,sat,}q} + \tfrac{1}{2} \left| u_p \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right) - \text{max}\left(-\gamma_{pq},0\right) \left(h_{\text{P,}q} + \tfrac{1}{2} \left| u_q \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right)\right] dV</math>|<xr id="eqn:TotalEnthalpyConservation10" nolink />}} | ||
| + | ::::<math>= \left[\text{max}\left(\Gamma_{pq},0\right) \left(h_{\text{P,sat,}q} + \tfrac{1}{2} \left| u_p \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right) - \text{max}\left(-\Gamma_{pq},0\right) \left(h_{\text{P,}q} + \tfrac{1}{2} \left| u_q \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right)\right] </math> | ||
</equation> | </equation> | ||
Revision as of 15:14, 19 April 2018
Conservation of Mass
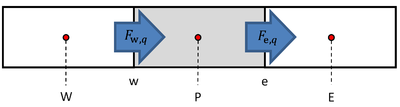
Steady one-dimensional conservation of mass (of phase q) is given through the following relation
-
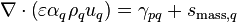
(1)
Equation 1 is discretized for an interior cell, shown in Figure 1, by volume integration over cell P.
-
![\Leftrightarrow \iiint\limits_V \left[\nabla\cdot\left(\varepsilon \alpha_q \rho_q u_q\right)\right]\, dV = \iiint\limits_V \left(\gamma_{pq} + s_{\text{mass},q}\right)\, dV](/kraken/images/math/f/4/8/f48e71d6341607aabdfacab6e554b84f.png)
(2)
The divergence term on the left-hand side of the equation is transformed into a surface integral over the cell faces using the divergence theorem.
-
![\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q u_q\right)\cdot n\right]\, dA = \iiint\limits_V \left(\gamma_{pq} + s_{\text{mass},q}\right)\, dV](/kraken/images/math/7/3/1/7310e052b999f6214874bb1e2314304b.png)
(3)
Throughout this document upwind discretization is used to evaluate the face mass flow rates, even though any discretization scheme could be chosen. The final discretized form reduces to
-
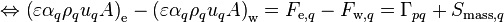
(4)
where:
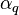
volume fraction of phase q [-], 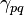
volumetric mass transfer rate from phase p to q [kg/m3s], 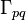
mass transfer rate from phase p to q [kg/s], 
porosity, fluid fraction of cell volume [-], 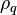
density of phase q [kg/m3], 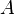
face area [m2], 
face mass flow rate [kg/s], 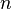
face normal pointing out of the cell (1 for east face, -1 for west face), 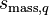
volumetric mass source to phase q [kg/m3s], 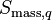
mass source to phase q [kg/s], 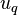
velocity of phase q [m/s], subscript e east face (the face in the negative x-direction), subscript w west face (the face in the positive x-direction), subscript q current phase for which the equation is written (1 = primary, 2 = secondary), subscript p the other phase (p = 2 for q = 1 and p = 1 for q = 2), subscript pq indicates exchange between phases (e.g. 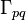 mass transfer from phase p to q).
mass transfer from phase p to q).
Conservation of Momentum
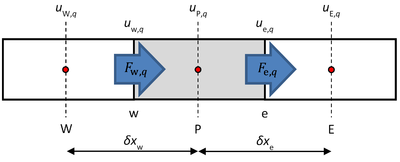
Steady one-dimensional conservation of momentum (of phase q) is solved from the following relation
-
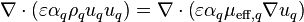
(5)
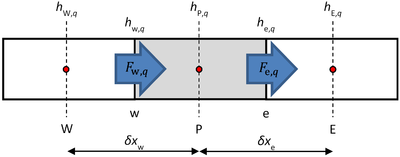
Equation 5 is discretized for an interior cell, shown in Figure 2, by volume integration over cell P. The diffusion term has been moved to the left-hand side, since it will be developed together with the divergence of momentum.
-
![\Leftrightarrow \iiint\limits_V \left[\nabla\cdot\left(\varepsilon \alpha_q \rho_q u_q u_q\right) - \nabla\cdot\left(\varepsilon \alpha_q \mu_{\text{eff},q} \nabla u_q\right)\right]\, dV = \iiint\limits_V \left[\text{max}\left(\gamma_{pq},0\right)u_p - \text{max}\left(-\gamma_{pq},0\right)u_q\right]\, dV](/kraken/images/math/b/2/7/b2712c69b3857c712df229a97d45e20b.png)
(6)
As with the conservation of mass equation above, the divergence terms on the left-hand side of the equation are transformed into surface integrals over the cell faces using the divergence theorem.
-
![\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q u_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \mu_{\text{eff},q} \frac{\Delta u_q}{\delta x}\right)\cdot n\right]\, dA = \left[\text{max}\left(\Gamma_{pq},0\right)u_p - \text{max}\left(-\Gamma_{pq},0\right)u_q\right]](/kraken/images/math/e/3/8/e380e70fef758530e299ea0acab2a7ee.png)
(7)
Developing the left-hand side terms first
-
![\iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q u_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \mu_{\text{eff},q} \frac{\Delta u_q}{\delta x}\right)\cdot n\right]\, dA](/kraken/images/math/4/4/f/44f02646928557013408bb2fcb86b0e2.png)
(8)
Adopting upwind discretization for the momentum fluxes on the cell faces
-
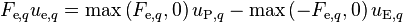
(9)
-
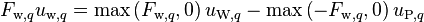
(10)
and rearranging terms
-
![\Leftrightarrow\iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q u_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \mu_{\text{eff},q} \frac{\Delta u_q}{\delta x}\right)\cdot n\right]\, dA](/kraken/images/math/7/d/5/7d5de0f19be966a3f775f91c30899a2c.png)
(11)
Denoting 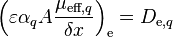 and
and 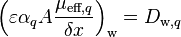 and modifying the central coefficient slightly, since
and modifying the central coefficient slightly, since 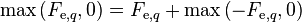 and
and 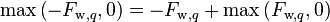 , Equation 11 reduces to
, Equation 11 reduces to
-
![\Leftrightarrow\iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q u_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \mu_{\text{eff},q} \frac{\Delta u_q}{\delta x}\right)\cdot n\right]\, dA](/kraken/images/math/7/d/5/7d5de0f19be966a3f775f91c30899a2c.png)
(12)
Identifying the coefficients of neighboring velocities
-
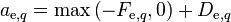
(13)
-
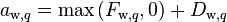
(14)
leads to a general form
-
![\Leftrightarrow\iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q u_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \mu_{\text{eff},q} \frac{\Delta u_q}{\delta x}\right)\cdot n\right]\, dA](/kraken/images/math/7/d/5/7d5de0f19be966a3f775f91c30899a2c.png)
(15)
Substituting the results of Equation 15 into Equation 7 and continuing with the development
-
![\Rightarrow\left[a_{\text{e},q} + a_{\text{w},q} + \left(F_{\text{e},q} - F_{\text{w},q}\right)\right]u_{\text{P},q} - a_{\text{e},q}u_{\text{E},q} - a_{\text{w},q}u_{\text{W},q}](/kraken/images/math/a/1/f/a1fa90c3136e1fb0a88bb43780b8e057.png)
(16)
At this point, the conservation of mass equation times cell velocity, 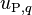 , is subtracted from Equation 16
, is subtracted from Equation 16
-
![\Rightarrow\left[a_{\text{e},q} + a_{\text{w},q} + \left(F_{\text{e},q} - F_{\text{w},q}\right) - \left(F_{\text{e},q} - F_{\text{w},q}\right)\right]u_{\text{P},q} - a_{\text{e},q}u_{\text{E},q} - a_{\text{w},q}u_{\text{W},q}](/kraken/images/math/d/a/2/da2a247d8ef6a063d9411ae2a21910f1.png)
(17)
Splitting the mass source term
-
![\Leftrightarrow\left[a_{\text{e},q} + a_{\text{w},q}\right]u_{\text{P},q} - a_{\text{e},q}u_{\text{E},q} - a_{\text{w},q}u_{\text{W},q}](/kraken/images/math/7/9/8/798ff496cdad3f190128786f0082a3d4.png)
(18)
-
![\Leftrightarrow\left[a_{\text{e},q} + a_{\text{w},q} + \text{max}\left(\Gamma_{pq},0\right) + \text{max}\left(S_{\text{mass},q},0\right) + \text{max}\left(-\Gamma_{pq},0\right)\right]u_{\text{P},q} - a_{\text{e},q}u_{\text{E},q} - a_{\text{w},q}u_{\text{W},q}](/kraken/images/math/9/d/4/9d4c1ac8d4b129ea8c226ede11042aaa.png)
(19)
Since the right-hand side contains only references to the central cell, subscripts P have been dropped from right-hand side to simplify the notation. Note that the diagonal element of the coefficient matrix contains the split terms, 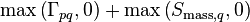 , resulting from the subtraction of the mass equation times cell velocity, while the counterparts,
, resulting from the subtraction of the mass equation times cell velocity, while the counterparts, ![\left[\text{max}\left(-\Gamma_{pq},0\right) + \text{max}\left(-S_{\text{mass},q},0\right)\right]u_q](/kraken/images/math/f/e/a/fea79e1112ad0a4cdd9ecaaae42e9492.png) , remain on the right-hand side. These are not considered as momentum source terms, as such, since they are only artifacts of the derivation procedure.
, remain on the right-hand side. These are not considered as momentum source terms, as such, since they are only artifacts of the derivation procedure.
Finally, denoting the central coefficient by 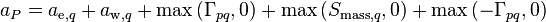 and casting Equation 19 into a vector form (over the phases) the final form, in which the equations are actually solved, is obtained. For simplicity’s sake, the equation is written only for the first 3 cells (c1, c2 and c3).
and casting Equation 19 into a vector form (over the phases) the final form, in which the equations are actually solved, is obtained. For simplicity’s sake, the equation is written only for the first 3 cells (c1, c2 and c3).
-
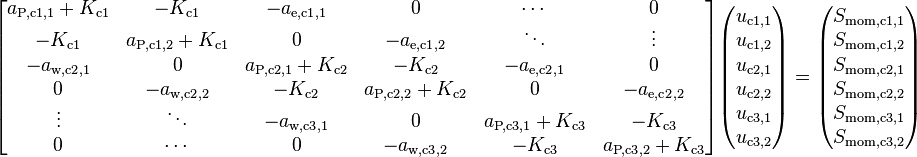
(20)
where:
and
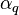
volume fraction of phase q [-], 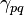
volumetric mass transfer rate from phase p to q [kg/m3s], 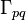
mass transfer rate from phase p to q [kg/s], 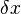
distance between two adjacent cell centers [m], 
porosity, fluid fraction of cell volume [-], 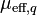
effective viscosity of phase q [Ns/m2], 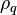
density of phase q [kg/m3], 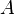
face area [m2], 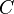
inertial loss coefficient [1/m], 
face mass flow rate [kg/s], 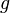
acceleration of gravity [m/s2], 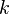
volumetric interphase drag coefficient [kg/m3s], 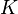
interphase drag coefficient [kg/s], 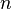
face normal pointing out of the cell (1 for east face, -1 for west face), 
pressure [Pa], 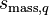
volumetric mass source to phase q [kg/m3s], 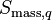
mass source to phase q [kg/s], 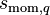
volumetric momentum source to phase q [N/m3], 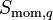
momentum source to phase q [N], 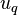
velocity of phase q [m/s], 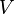
cell volume [m3], subscript c1 refers to first cell, subscript c2 refers to second cell, subscript c3 refers to third cell, subscript e east face (the face in the negative x-direction), subscript E east neighbor (the cell in the negative x-direction), subscript w west face (the face in the positive x-direction), subscript W west neighbor (the cell in the positive x-direction), subscript P central cell (the cell for which the equation is written), subscript q current phase for which the equation is written (1 = primary, 2 = secondary), subscript p the other phase (p = 2 for q = 1 and p = 1 for q = 2), subscript pq indicates exchange between phases (e.g. 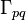 mass transfer from phase p to q).
mass transfer from phase p to q).
Conservation of Total Enthalpy
Conservation of total enthalpy (of phase q) can be written as
-
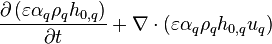
(21)
Disregarding the transient terms and moving the diffusion term to the left-hand side leads to
-
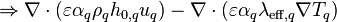
(22)
Total enthalpy is defined as the sum of specific enthalpy, kinetic energy and potential energy
-
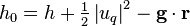
(23)
where 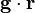 is the dot product of gravity vector,
is the dot product of gravity vector, 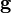 , and location vector,
, and location vector, 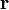 , a vector pointing from the reference level to the evaluated location. The total enthalpies related to phase change can be defined as
, a vector pointing from the reference level to the evaluated location. The total enthalpies related to phase change can be defined as
-
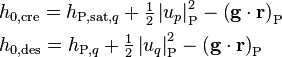
(24)
In other words, when mass is transferred to phase q (“created”), it brings with it the saturation enthalpy of phase q, 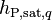 , and the kinetic energy of phase p,
, and the kinetic energy of phase p, 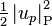 . When mass is transferred from phase q (“destroyed”), it leaves with the enthalpy and kinetic energy of phase q,
. When mass is transferred from phase q (“destroyed”), it leaves with the enthalpy and kinetic energy of phase q, 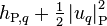 . It is chosen that the potential energy associated with phase change is evaluated at the center of the cell,
. It is chosen that the potential energy associated with phase change is evaluated at the center of the cell,  .
.
Substituting Equation 23 and Equation 24 to Equation 22 and rearranging terms
-
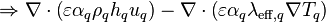
(25)
At this point, an approximation is introduced: the diffusion term is expressed relative to the gradient of enthalpy, instead of temperature, as follows. This approximation is considered to be sufficiently accurate for small enthalpy differences.
-
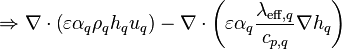
(26)
Equation 26 is discretized for an interior cell, shown in Figure 3, by volume integration over cell P.
-
![\Leftrightarrow \iiint\limits_V \left[\nabla\cdot\left(\varepsilon \alpha_q \rho_q h_q u_q\right) - \nabla\cdot\left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \nabla h_q \right)\right]\, dV](/kraken/images/math/d/e/d/ded1be6ed9cf382366806e0aafe75b5d.png)
(27)
As with the conservation of mass and momentum above, the divergence terms on the left-hand side of the equation are transformed into surface integrals over the cell faces using the divergence theorem.
-
![\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q h_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \frac{\Delta h_q}{\delta x}\right)\cdot n\right]\, dA](/kraken/images/math/9/1/5/915ed57c73cdf169081447e4379a8458.png)
(28)
Developing the left-hand side first.
-
![\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q h_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \frac{\Delta h_q}{\delta x}\right)\cdot n\right]\, dA](/kraken/images/math/9/1/5/915ed57c73cdf169081447e4379a8458.png)
(29)
Adopting upwind discretization for the enthalpy fluxes on the cell faces
-
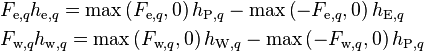
(30)
and rearranging terms
-
![\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q h_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \frac{\Delta h_q}{\delta x}\right)\cdot n\right]\, dA](/kraken/images/math/9/1/5/915ed57c73cdf169081447e4379a8458.png)
(31)
Denoting 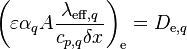 and
and 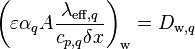 and modifying the central coefficient slightly, since
and modifying the central coefficient slightly, since 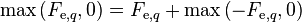 and
and 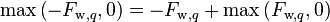 , Equation 31 reduces to
, Equation 31 reduces to
-
![\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q h_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \frac{\Delta h_q}{\delta x}\right)\cdot n\right]\, dA](/kraken/images/math/9/1/5/915ed57c73cdf169081447e4379a8458.png)
(32)
Identifying the coefficients of neighboring velocities as
-
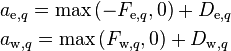
(33)
leads to a general form
-
![\Leftrightarrow \iint\limits_{A}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset \left[\left(\varepsilon \alpha_q \rho_q h_q u_q\right)\cdot n - \left(\varepsilon \alpha_q \frac{\lambda_{\text{eff},q}}{c_{p,q}} \frac{\Delta h_q}{\delta x}\right)\cdot n\right]\, dA](/kraken/images/math/9/1/5/915ed57c73cdf169081447e4379a8458.png)
(34)
Substituting the results of Equation 34 into Equation 28 and continuing with the development
-
![\Rightarrow \left[ a_{\text{e},q} + a_{\text{w},q} + \left( F_{\text{e},q} - F_{\text{w},q} \right) \right] h_{\text{P},q} - a_{\text{e},q} h_{\text{E},q} - a_{\text{w},q} h_{\text{W},q}\, dA](/kraken/images/math/f/7/6/f764c80377244835797eebd1581733d5.png)
(36)
Integrating the right-hand side term by term. The phase change term reduces to
-
![\iiint\limits_V \left[\text{max}\left(\gamma_{pq},0\right) \left(h_{\text{P,sat,}q} + \tfrac{1}{2} \left| u_p \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right) - \text{max}\left(-\gamma_{pq},0\right) \left(h_{\text{P,}q} + \tfrac{1}{2} \left| u_q \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right)\right] dV](/kraken/images/math/c/e/0/ce044f40316f4ddff3429b1c6d8bc3c8.png)
(36)
![+ \left[\text{max}\left(\gamma_{pq},0\right)u_p - \text{max}\left(-\gamma_{pq},0\right)u_q\right] - \varepsilon \alpha_q \nabla p + \varepsilon \alpha_q \rho_q g](/kraken/images/math/c/b/9/cb9318a7fbaaaa3c856ffaf9005d05a4.png)
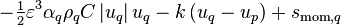
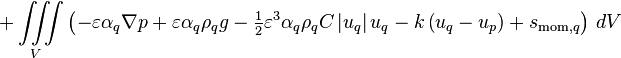
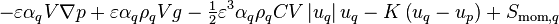

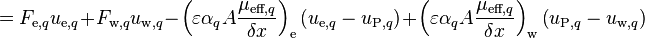
![=\left[\text{max}\left(F_{\text{e},q},0\right) + \text{max}\left(-F_{\text{w},q},0\right) + \left(\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x}\right)_{\text{e}} + \left(\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x}\right)_{\text{w}}\right]u_{\text{P},q}](/kraken/images/math/3/9/9/399ef53f0abeac0473ca93e7977fac80.png)
![-\left[\text{max}\left(-F_{\text{e},q},0\right) + \left(\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x}\right)_{\text{e}}\right]u_{\text{E},q}](/kraken/images/math/6/b/3/6b31631c9deb28335c375c06a3d0d030.png)
![-\left[\text{max}\left(F_{\text{w},q},0\right) + \left(\varepsilon \alpha_q A \frac{\mu_{\text{eff},q}}{\delta x}\right)_{\text{w}}\right]u_{\text{W},q}](/kraken/images/math/b/e/e/bee9892fe30fa349bdb304bf7775ffc8.png)
![= \left[\text{max}\left(-F_{\text{e},q},0\right) + D_{\text{e},q} + \text{max}\left(F_{\text{w},q},0\right) + D_{\text{w},q} + \left(F_{\text{e},q} - F_{\text{w},q}\right)\right]u_{\text{P},q}](/kraken/images/math/6/a/1/6a14c9996a6210d0e6cd00faf571de77.png)
![-\left[\text{max}\left(-F_{\text{e},q},0\right) + D_{\text{e},q}\right]u_{\text{E},q} - \left[\text{max}\left(F_{\text{w},q},0\right) + D_{\text{w},q}\right]u_{\text{W},q}](/kraken/images/math/8/4/5/845bc7a2f0606db36b351968e43f48dc.png)
![= \left[a_{\text{e},q} + a_{\text{w},q} + \left(F_{\text{e},q} - F_{\text{w},q}\right)\right]u_{\text{P},q} - a_{\text{e},q}u_{\text{E},q} - a_{\text{w},q}u_{\text{W},q}](/kraken/images/math/9/f/1/9f18c89b7e860a7008e2c3c14d212be7.png)
![= \left[\text{max}\left(\Gamma_{pq},0\right)u_p - \text{max}\left(-\Gamma_{pq},0\right)u_q\right] - \varepsilon \alpha_q V \nabla p + \varepsilon \alpha_q \rho_q V g](/kraken/images/math/6/e/6/6e6339c3a814a64f32d7fbae576cd0f5.png)
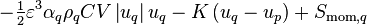
![= \left[\text{max}\left(\Gamma_{pq},0\right)u_p - \text{max}\left(-\Gamma_{pq},0\right)u_q\right] - \left(\Gamma_{pq} + S_{\text{mass},q}\right)u_{\text{P},q}](/kraken/images/math/3/b/5/3b5b23c7e405935814c27671016cf3c7.png)
![= \left[\text{max}\left(\Gamma_{pq},0\right)u_{\text{P},p} - \text{max}\left(-\Gamma_{pq},0\right)u_{\text{P},q}\right]](/kraken/images/math/8/8/8/888e32a31eaccebdb6e64f843664cf73.png)
![-\left[\text{max}\left(\Gamma_{pq},0\right) - \text{max}\left(-\Gamma_{pq},0\right) + \text{max}\left(S_{\text{mass},q},0\right) - \text{max}\left(-S_{\text{mass},q},0\right)\right]u_{\text{P},q}](/kraken/images/math/7/2/7/72744f41c842afd2c31892b167d36043.png)
![= \left[\text{max}\left(-\Gamma_{pq},0\right) + \text{max}\left(-S_{\text{mass},q},0\right)\right]u_q + \text{max}\left(\Gamma_{pq},0\right)u_p](/kraken/images/math/4/c/8/4c836d593aa8f252d8c50cdf3a143b27.png)
![S_{\text{mom},\text{c1},q} = \Big\{\big[\text{max}\left(-\Gamma_{pq},0\right) + \text{max}\left(-S_{\text{mass},q},0\right)\big]u_q + \text{max}\left(\Gamma_{pq},0\right)u_p](/kraken/images/math/2/7/f/27f7e9dbad96996d7d7cfc763fb39e12.png)
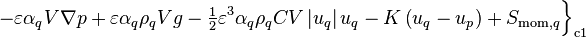
![= \nabla\cdot\left(\varepsilon \alpha_q \lambda_{\text{eff},q} \nabla T_q \right) + \left[\text{max}\left(\gamma_{pq},0\right) h_{0,\text{cre}} - \text{max}\left(-\gamma_{pq},0\right) h_{0,\text{des}}\right]](/kraken/images/math/f/d/d/fdd7504ef94955b652efccf6553d3a0e.png)
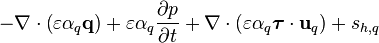
![= \left[\text{max}\left(\gamma_{pq},0\right) h_{0,\text{cre}} - \text{max}\left(-\gamma_{pq},0\right) h_{0,\text{des}}\right] - \nabla\cdot\left(\varepsilon \alpha_q \mathbf{q} \right) + \nabla\cdot\left(\varepsilon \alpha_q \boldsymbol{\tau} \cdot \mathbf{u}_q \right) + s_{h,q}](/kraken/images/math/a/5/7/a57e9b9ee32ff5d733461f3580589d60.png)
![= \left[\text{max}\left(\gamma_{pq},0\right) \left(h_{\text{P,sat,}q} + \tfrac{1}{2} \left| u_p \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right) - \text{max}\left(-\gamma_{pq},0\right) \left(h_{\text{P,}q} + \tfrac{1}{2} \left| u_q \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}
\right)\right]](/kraken/images/math/4/6/f/46fe563fa8f9fd8a50836ed1e5d01adb.png)
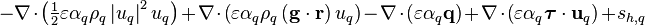
![= \iiint\limits_V \Big\{ \left[\text{max}\left(\gamma_{pq},0\right) \left(h_{\text{P,sat,}q} + \tfrac{1}{2} \left| u_p \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right) - \text{max}\left(-\gamma_{pq},0\right) \left(h_{\text{P,}q} + \tfrac{1}{2} \left| u_q \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right)\right]](/kraken/images/math/0/2/d/02d773d05b3277198585d15573db3e39.png)
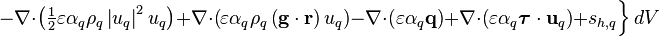


![= \left[ \text{max}\left(F_{\text{e},q},0\right) + \text{max}\left(-F_{\text{w},q},0\right) + \left(\varepsilon \alpha_q A \frac{\lambda_{\text{eff},q}}{c_{p,q}\delta x}\right)_{\text{e}} + \left(\varepsilon \alpha_q A \frac{\lambda_{\text{eff},q}}{c_{p,q}\delta x}\right)_{\text{w}} \right] h_{\text{P},q}](/kraken/images/math/b/7/c/b7cd5ddaf5739424a772224ad76c435d.png)
![- \left[ \text{max}\left(-F_{\text{e},q},0\right) + \left(\varepsilon \alpha_q A \frac{\lambda_{\text{eff},q}}{c_{p,q}\delta x}\right)_{\text{e}} \right] h_{\text{E},q} - \left[ \text{max}\left(F_{\text{w},q},0\right) + \left(\varepsilon \alpha_q A \frac{\lambda_{\text{eff},q}}{c_{p,q}\delta x}\right)_{\text{w}} \right] h_{\text{W},q}](/kraken/images/math/5/6/3/563ccf430a94c716f3f2bea92515becf.png)
![= \left[ \text{max}\left(-F_{\text{e},q},0\right) + D_{\text{e},q} + \text{max}\left(F_{\text{w},q},0\right) + D_{\text{w},q} + \left( F_{\text{e},q} - F_{\text{w},q} \right) \right] h_{\text{P},q}](/kraken/images/math/e/2/b/e2bce9cdc7a6b6f9761cdb2da5370d22.png)
![- \left[ \text{max}\left(-F_{\text{e},q},0\right) + D_{\text{e},q} \right] h_{\text{E},q}
- \left[ \text{max}\left(F_{\text{w},q},0\right) + D_{\text{w},q} \right] h_{\text{W},q}](/kraken/images/math/7/a/8/7a8ff932eeb0976faa4491f20159b29e.png)
![= \left[ a_{\text{e},q} + a_{\text{w},q} + \left( F_{\text{e},q} - F_{\text{w},q} \right) \right] h_{\text{P},q} - a_{\text{e},q} h_{\text{E},q} - a_{\text{w},q} h_{\text{W},q}](/kraken/images/math/7/f/3/7f3d736f0dc96567420cd56623265fb4.png)
![= \left[\text{max}\left(\Gamma_{pq},0\right) \left(h_{\text{P,sat,}q} + \tfrac{1}{2} \left| u_p \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right) - \text{max}\left(-\Gamma_{pq},0\right) \left(h_{\text{P,}q} + \tfrac{1}{2} \left| u_q \right|^2_{\text{P}} - \left(\mathbf{g} \cdot \mathbf{r}\right)_{\text{P}}\right)\right]](/kraken/images/math/3/d/5/3d5e238b6b16cc5bef8146947459d126.png)