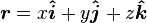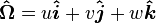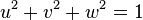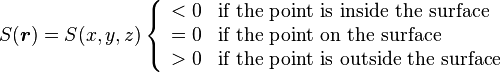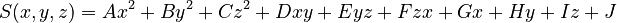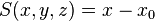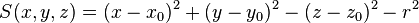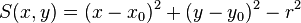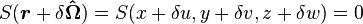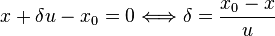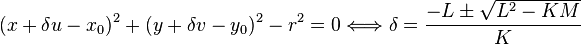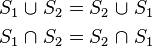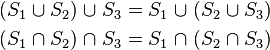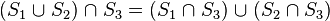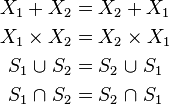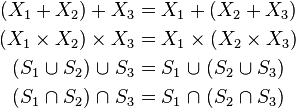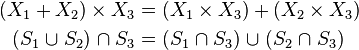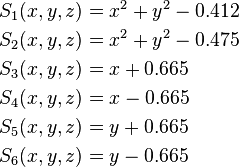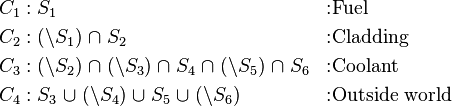Difference between revisions of "Universe-based geometry type in Serpent"
(→Cells) |
|||
| Line 34: | Line 34: | ||
z-axis, respectively. | z-axis, respectively. | ||
| − | = Basic building blocks = | + | == Basic building blocks == |
| − | == Surfaces == | + | === Surfaces === |
Monte Carlo transport codes are most typically based on the constructive solid geometry (CSG) type, in which the geometry is composed of homogeneous material cells, defined using combinations of elementary and derived surface types. | Monte Carlo transport codes are most typically based on the constructive solid geometry (CSG) type, in which the geometry is composed of homogeneous material cells, defined using combinations of elementary and derived surface types. | ||
| Line 114: | Line 114: | ||
where <math>K = u^2 + v^2</math>, <math>L = u(x - x_0) + v(y - y_0)</math> and <math>M = (x - x_0)^2 + (y - y_0)^2 - r^2</math>. | where <math>K = u^2 + v^2</math>, <math>L = u(x - x_0) + v(y - y_0)</math> and <math>M = (x - x_0)^2 + (y - y_0)^2 - r^2</math>. | ||
| − | == Cells == | + | === Cells === |
The next building block in the CSG hierarchy is the cell, which is constructed from the combination of surfaces, and it defines a homogeneous material region. The construction is based on three operators: | The next building block in the CSG hierarchy is the cell, which is constructed from the combination of surfaces, and it defines a homogeneous material region. The construction is based on three operators: | ||
| Line 219: | Line 219: | ||
The last cell, described as the "outside world", is not a part of the actual geometry, but it needs to be defined in order to tell the geometry routine that the particle has escaped the system, or that boundary conditions need to be invoked. | The last cell, described as the "outside world", is not a part of the actual geometry, but it needs to be defined in order to tell the geometry routine that the particle has escaped the system, or that boundary conditions need to be invoked. | ||
| − | = Universes and lattices = | + | == Universes and lattices == |
Revision as of 21:35, 8 March 2016
From here on it is assumed that the tracking takes place in a three-dimensional Cartesian coordinate system. In vector notation, the position and direction of motion are defined by two vectors:
and
where 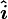 ,
, 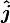 and
and 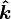 are the unit vectors defining the
three-dimensional Cartesian coordinate system. Direction vector
are the unit vectors defining the
three-dimensional Cartesian coordinate system. Direction vector 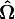 is normalized to unity:
is normalized to unity:
or
Coefficients 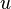 ,
, 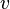 and
and 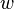 are the direction cosines, i.e. the
cosines of the angle that vector
are the direction cosines, i.e. the
cosines of the angle that vector 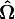 forms with the positive x-, y- and
z-axis, respectively.
forms with the positive x-, y- and
z-axis, respectively.
Basic building blocks
Surfaces
Monte Carlo transport codes are most typically based on the constructive solid geometry (CSG) type, in which the geometry is composed of homogeneous material cells, defined using combinations of elementary and derived surface types.
The most elemental building block is the surface, described using algebraic equations, typically of the quadratic type. The action that puts an arbitrary position 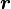 on one or the other side of a surface is based on a simple test carried out by substituting the coordinates into the surface equation:
on one or the other side of a surface is based on a simple test carried out by substituting the coordinates into the surface equation:
This surface test also fixes the concepts of ``inside and ``outside for each surface type, which is important when forming the cells from the surface combinations.
The general quadratic surface can be written in parametric form as:
where 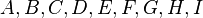 and
and 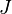 are constants. Common examples of quadratic surfaces obtained from the parametrized
quadratic equation include the plane perpendicular to x-axis at
are constants. Common examples of quadratic surfaces obtained from the parametrized
quadratic equation include the plane perpendicular to x-axis at 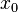 :
:
sphere centered at 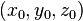 with radius
with radius  :
:
and straight infinite cylinder parallel to z-axis centered at 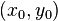 with
radius
with
radius  :
:
There are also non-quadratic surfaces, such as the torus, for which the surface test cannot be performed by substituting the coordinates into a single equation.
Monte Carlo codes often provide additional derived surface types, which are formed by combinations of elementary surfaces. For example, a cuboid with boundaries ![[x_1, x_2]](/mediawiki/images/math/4/8/f/48f0a3fbaaf45d915fd69980c25b8d48.png) ,
, ![[y_1, y_2]](/mediawiki/images/math/f/5/6/f566d7f5633dbeefbec3135e9ea5ea8b.png) ,
, ![[z_1, z_2]](/mediawiki/images/math/4/7/c/47c382df164109d1de70a5c7d7311698.png) consists of six planes perpendicular to the coordinate axes, and surface test works by testing the position of the point with respect to all of them. Other derived surface types convenient for reactor modeling include truncated cylinders, and square and hexagonal prisms.
consists of six planes perpendicular to the coordinate axes, and surface test works by testing the position of the point with respect to all of them. Other derived surface types convenient for reactor modeling include truncated cylinders, and square and hexagonal prisms.
Surface equations are also used for determining the distance to the nearest material boundary in the direction of motion. The points where the particle path intersects the surface are obtained by solving the surface equation with condition:
i.e. by setting a point located at distance 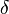 from position
from position 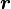 in the direction of motion
in the direction of motion 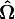 on the surface, and solving for
on the surface, and solving for 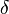 . When the equation has multiple solutions, the nearest point corresponds to the smallest positive value of
. When the equation has multiple solutions, the nearest point corresponds to the smallest positive value of 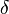 . If all solutions are negative or no solution exists, the surface is away from the line-of-sight.
. If all solutions are negative or no solution exists, the surface is away from the line-of-sight.
As an example, the distance to a plane perpendicular to x-axis at 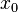 is obtained from
is obtained from
and the distance to a straight infinite cylinder parallel to z-axis centered at 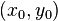 with radius
with radius  from:
from:
where 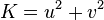 ,
, 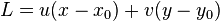 and
and 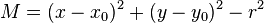 .
.
Cells
The next building block in the CSG hierarchy is the cell, which is constructed from the combination of surfaces, and it defines a homogeneous material region. The construction is based on three operators:
- Intersection :
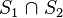 - Point is inside the cell if it is inside both surface
- Point is inside the cell if it is inside both surface 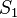 and
and 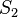
- Union :
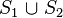 - Point is inside the cell if it is inside either surface
- Point is inside the cell if it is inside either surface 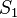 or
or 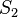 , or both
, or both - Complement :
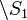 - Point is inside the cell if it is outside surface
- Point is inside the cell if it is outside surface 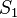
The intersection and union operator behave very similar to arithmetic multiplication and addition, respectively, and they share the properties of commutativity (order of operands is exchangeable):
associativity (two or more similar operations can be grouped in an arbitrary manner):
and distributivity (precedence of intersection over union):
The analogies to arithmetic operations are best illustrated by examples (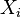 are real numbers).
are real numbers).
Consider a 2D pin-cell model of a light water reactor fuel pin surrounded by coolant. The pin consist of a fuel pellet with an outer diameter of 0.824 cm, enclosed inside a 0.063 cm thick cladding. The square pitch of the unit cell is 1.330 cm. The surfaces are defined as:
These surfaces are used to define four cells using intersections, unions and complements:
The last cell, described as the "outside world", is not a part of the actual geometry, but it needs to be defined in order to tell the geometry routine that the particle has escaped the system, or that boundary conditions need to be invoked.