Difference between revisions of "Result estimators"
m |
Ana Jambrina (Talk | contribs) (→Collision flux estimator (CFE)) |
||
| Line 87: | Line 87: | ||
was used for sampling the path length. It should be noted that with [[Delta- and surface-tracking#Transport algorithms in Monte Carlo simulation|delta-tracking]] this cross section is not necessarily the physical material total. | was used for sampling the path length. It should be noted that with [[Delta- and surface-tracking#Transport algorithms in Monte Carlo simulation|delta-tracking]] this cross section is not necessarily the physical material total. | ||
| − | Serpent uses the CFE for all integral result estimates, including the common detector types. The scores are based on physical collisions. Virtual collisions are included if the material total cross section falls below a pre-defined limit. This is to ensure a sufficient collision rate in low density materials. The limit can be adjusted using the [[Input syntax manual#set | + | Serpent uses the CFE for all integral result estimates, including the common detector types. The scores are based on physical collisions. Virtual collisions are included if the material total cross section falls below a pre-defined limit. This is to ensure a sufficient collision rate in low density materials. The limit can be adjusted using the [[Input syntax manual#set cfe|set cfe]] input option. |
=== Track-length flux estimator (TLE) === | === Track-length flux estimator (TLE) === | ||
Revision as of 15:18, 26 May 2022
The Monte Carlo transport simulation is run to obtain statistical estimates for integrals of the form:
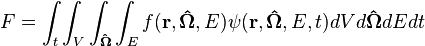
where 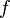 is a response function that can be evaluated at an arbitrary position
of the phase space, most typically a reaction cross section. These estimates
are based on the collection of simulated events (collisions, track-lengths,
surface crossings, etc.) that occur during the course of the simulated
random walk.
is a response function that can be evaluated at an arbitrary position
of the phase space, most typically a reaction cross section. These estimates
are based on the collection of simulated events (collisions, track-lengths,
surface crossings, etc.) that occur during the course of the simulated
random walk.
The estimates can be divided into:
- Analog estimates, based on recorded simulated physical events
- Implicit estimators, based the expected frequency of events
Implicit estimators are derived from analog estimators, with the purpose of obtaining better statistics.
Contents
Analog estimators
Analog estimates are the most straightforward way to obtain physical results from the Monte Carlo transport simulation. Each particle history consists of a number of events containing relevant information on the transport process, which can be counted as-is, for example:
- Collisions
- Sampled reactions
- Crossed surfaces
- Neutrons emitted in fission
The integration domain is defined by separating the scores into different bins based on particle position, energy and time (and direction of motion). For example:
- Fission rate in a specific fuel pin -- count the number of simulated fission events in that fuel pin (integration over specific volume)
- Thermal neutron absorption in coolant -- count the number of neutrons absorbed in the coolant with energy in the thermal region (integration over specific volume and energy)
- Total fission rate as function of time -- count the number of fissions, and place the results in successive bins depending on the time of the event (integration over specific time)
These examples also illustrate the fact the results are always integrated over the variables.
Examples of analog estimators used by Serpent 2 include:
- The analog estimate of keff (ANA_KEFF), given by the ratio of produced and starting population weight in each generation. The estimate is calculated separately for for new fission neutrons produced by all, prompt and delayed neutrons.
- Analog reaction rate estimators calculated by counting the number of sampled reactions (invoked by option set arr).
- Surface current detector
Analog estimator is also used to collect data on scattering events for the scattering matrices.
Implicit estimators
Implicit estimators are derived from analog estimators, but instead of scoring events that actually occured during the simulation, the estimates are based on the expected occurrance of the evens. The implicit estimators used in Serpent 2 are listed below.
Collision flux estimator (CFE)
Implicit estimators are best understood by considering
the collision estimate of particle flux (CFE). When a collision occurs at a given position,
the probability of sampling reaction 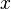 is the ratio of the reaction cross section to material total:
is the ratio of the reaction cross section to material total:
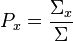
The probability is the same whether the reaction was actually sampled or not,
so counting 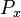 as the result estimate means that the
overall score reflects the statistically expected number of reactions
as the result estimate means that the
overall score reflects the statistically expected number of reactions 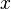 .
.
Since the total number of collisions is always greater than or equal to the number of sampled reactions, the implicit estimator gives better statistics. The overall score is given by the sum over all collisions:
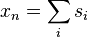
where the CFE is written as:
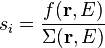
and 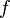 is the response function and
is the response function and 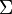 is the cross section that
was used for sampling the path length. It should be noted that with delta-tracking this cross section is not necessarily the physical material total.
is the cross section that
was used for sampling the path length. It should be noted that with delta-tracking this cross section is not necessarily the physical material total.
Serpent uses the CFE for all integral result estimates, including the common detector types. The scores are based on physical collisions. Virtual collisions are included if the material total cross section falls below a pre-defined limit. This is to ensure a sufficient collision rate in low density materials. The limit can be adjusted using the set cfe input option.
Track-length flux estimator (TLE)
Another commonly used implicit estimator is the track-length estimate of neutron flux (TLE), which is based on the collection of neutron tracks. The overall score is given by the sum over all tracks:
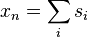
where the TLE is written as:
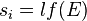
and 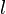 is the path length traveled by the neutron between collisions
and surface crossings. The relation to flux is seen in that the
integral flux is equal to the sum of total path lengths traveled by
neutrons in the medium.
is the path length traveled by the neutron between collisions
and surface crossings. The relation to flux is seen in that the
integral flux is equal to the sum of total path lengths traveled by
neutrons in the medium.
The TLE can be used similar to CFE, but there are a few differences:
- Since TLE is scored each time the neutron passes through a region, whether it collides or not, the number of scores is always greater than or equal to that of the CFE.
- Since CFE is based on collisions that occur in discrete points in space, it can be used for calculating reaction rates in inhomogeneous material regions.
Most Monte Carlo codes rely on the use of track-length estimators, because of their superior performance. The differences are emphasized in a few specific cases:
- Calculation of flux integrals in optically thin regions (high probability to pass through, low probability to collide).
- Calculation of reaction rates with high threshold energy (fission neutrons exiting the fuel pin always contribute to TLE but only rarely to CFE).
- Calculation of reaction rates in low density or void regions (few or zero collisions for CFE, although the problem can be overcome by introducing virtual collisions).
- Calculation of reaction rates in regions located far or isolated from the active source (already poor statistics).
Practical experience with has shown, however, that there is usually no major difference between the two estimators in reactor physics applications, in which reaction rates are most typically scored in regions of high collision rate near the active source.[1]
Because the transport algorithm in Serpent is based on delta-tracking (which does not account for surface crossings), the track-length estimator is not a practical choice for calculating integral reaction rates. The method is used only for super-imposed TLE and surface current detectors, and the calculation of surface fluxes and currents for assembly discontinuity factors.
References
- ^ Leppänen, J. "Performance of Woodcock delta-tracking in lattice physics applications using the Serpent Monte Carlo reactor physics burnup calculation code." Ann. Nucl. Energy 37 (2010) 715–722.