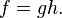Critical density iteration
This feature has been developed mainly to help in iterating the critical boron concentration for LWR systems, but can be used for various applications as long as the limitations of the methodology are well noted.
A set of nuclides in a set of materials can be flagged for critical density iteration, where the atomic density of the nuclides will be scaled using a multiplicative factor in such a way that the absorption of neutrons to the nuclides will bring the system critical.
Critical density iteration was first implemented in Serpent 2.1.29.
Contents
Input
set iter nuc CYCLES KEFF NZAI ZAI1 ZAI2 ... ZAINZAI [ NMAT MAT1 MAT2 ... MAXNMAT ]
| CYCLES | : number of additional inactive cycles to run for the convergence of the iteration |
| KEFF | : target k-eff for the iteration |
| NZAI | : number of different nuclides (ZAI) included in the iteration |
| ZAIi | : the ZAI (e.g. 50100 for boron 10 ground state) of the nuclide to be included in the iteration |
| NMAT | : number of different materials included in the iteration (optional parameter) |
| MATi | : the name of the material to be included in the iteration |
Notes:
- If a list of materials is not given, all materials that contain the included nuclides are included in the iteration.
- The initial density of the nuclides to be iterated should be larger than zero.
- The critical density iteration only works for nuclides that have a reactivity effect mainly through neutron absorption. Specifically, critical densities of fissile, moderating or reflecting nuclides cannot be reliably iterated using this card.
- The atomic density of the nuclides is updated according to the batching interval set in the set pop card. Having a large batching interval means that the atomic density may take a large number of cycles to converge.
Output
An output variable ITER_FACTOR is included in the main [INPUT]_res.m results file. The output variable gives the mean multiplicative scaling factor applied to the density of the iterated nuclides to achieve a critical system. The critical density of the nuclides can be obtained by reading the nuclide densities (atomic or mass) from the [input].out file for each included material and scaling them with the scaling factor while keeping the densities of other nuclides constant.
If the batch history recording is set on (see set his) the [INPUT]_his[STEP].m history output file will contain batch-wise estimates for the scaling factor, which can be used to ensure the convergence of the scaling factor during the inactive cycles.
Operation
- Serpent will first execute the inactive cycles defined using the set pop input option with a multiplicative scaling factor of 1.0.
- After that, the additional inactive cycles defined using set iter nuc will be executed and the multiplicative scaling factor will be updated after each cycle in order to bring the system to criticality.
- Finally, the active cycles will be executed with the scaling factor still updated after each cycle.
Implementation
During each neutron cycle, Serpent calculates the neutron loss due to absorption by the flagged nuclides 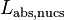 and tallies separately various neutron loss and neutron production terms.
and tallies separately various neutron loss and neutron production terms.
Starting from the k-eigenvalue form of the neutron balance equation for the system
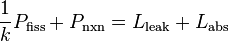
we can separate the absorption rate to two parts
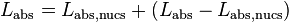
where the first term represents the loss to the flagged nuclides and the second term represents the loss to other nuclides. The neutron balance equation then becomes
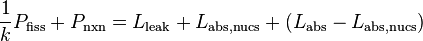 .
.
The objective is to find a neutron loss rate to the flagged nuclides 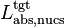 such that the k-effective of the system is the one we want to obtain
such that the k-effective of the system is the one we want to obtain 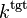 , e.g. 1.
, e.g. 1.
This yields the balance equation
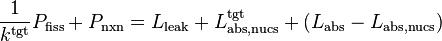 .
.
The critical absorption rate by the flagged nuclides is solved from
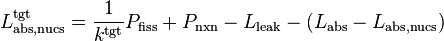
using the values tallied for each term during the previous transport cycle.
By assuming a linear dependence between the atomic densities of the flagged nuclides and their absorption rate, we see that the atomic densities should be scaled for the next cycle (relative to densities during previous cycle) with a factor of
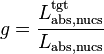
If the results for the previous cycle were obtained using a scaling factor of 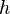 , the absolute scaling factor (relative to the initial densities) is
, the absolute scaling factor (relative to the initial densities) is