Difference between revisions of "Boundary conditions"
(→Boundary conditions in 2D geometries) |
|||
| Line 1: | Line 1: | ||
| − | + | Boundary conditions are invoked when the particle crosses the boundary from the defined part of the geometry into a region labeled as "outside" in the [[Input syntax manual#cell (cell definition)|cell cards]]. The outcome then depends on the boundary conditions, as defined by the "[[Input syntax manual#set bc|set bc]]" option. Serpent provides three types of boundary conditions: | |
| + | |||
| + | # Black boundary - the particle is killed | ||
| + | # Reflective boundary - the particle is reflected back into the geometry | ||
| + | # Periodic boundary - the particle is moved to the opposite side of the geometry | ||
| + | |||
| + | Reflective and periodic boundary conditions can be used to construct infinite and semi-infinite lattice structures. The way these boundary conditions are handled in Serpent is somewhat different from other Monte Carlo codes. Instead of stopping the neutron at the boundary surface, reflections and translations are handled by coordinate transformations. This limits the outermost boundary to a few specific surface types that form regular lattices. In 2D geometries such surfaces are: | ||
| + | |||
| + | *Square prism ("sqc") - forms a 2D square lattice | ||
| + | *Hexagonal prisms ("hexxc" and "hexxyc") -- form 2D hexagonal lattices | ||
| + | *Rectangular prism ("rect") - forms a 2D rectangular lattice | ||
| + | |||
| + | And in 3D: | ||
| + | |||
| + | *Cube ("cube") - forms a 3D cubical lattice | ||
| + | *Cuboid ("cuboid") - forms a 3D cuboidal lattice | ||
| + | *Truncated hexagonal prisms ("hexxprism" and "hexyprism") - form a 3D hexagonal lattices | ||
| + | |||
| + | Repeated boundary conditions are invoked only on the first surface listed in the "outside" type cells. Since the geometry boundary may consist of additional surfaces, some boundaries may be treated as reflective or periodic, while others are treated as vacuum. In reactor geometries there are typically three possible configurations: | ||
| + | |||
| + | ;Infinite 2D geometry: The geometry has no dependence on the z-coordinate. The outer boundary is defined by one of the 2D surfaces listed above. | ||
| + | ;Radially infinite, axially finite 3D geometry:The outer boundary is defined by one of the 2D surfaces listed above and two axial planes ("pz"). The boundary condition takes effect in the radial direction only, while the axial boundaries are vacuum. | ||
| + | ;Infinite 3D geometry: The outer boundary is defined by one of the 2D surfaces listed above. The boundary condition takes effect in all directions. | ||
| + | |||
| + | These configurations are demonstrated below. | ||
| + | |||
| + | |||
| + | == Infinite 2D geometries == | ||
| + | |||
| + | |||
| + | <gallery mode="nolines" widths=320px heights=320px> | ||
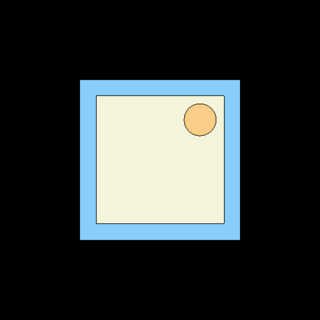
| + | Image:vacu2D.png|'''Vacuum boundary conditions''' ("set bc 1"). See [[media:vacu2D.gif|animated particle tracks]]. | ||
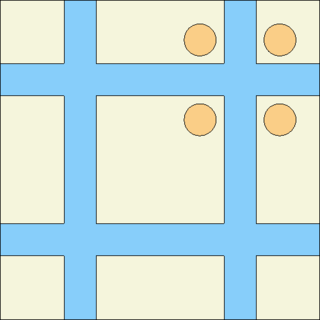
| + | Image:refl2D.png|'''Reflective boundary conditions''' ("set bc 2"). See [[media:refl2D.gif|animated particle tracks]]. | ||
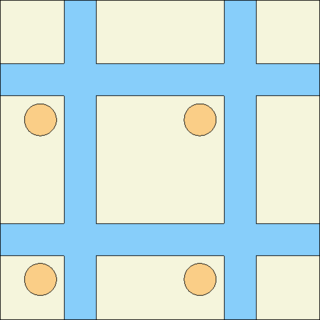
| + | Image:peri2D.png|'''Periodic boundary conditions''' ("set bc 3"). See [[media:peri2D.gif|animated particle tracks]]. | ||
| + | </gallery> | ||
| − | |||
| − | |||
| − | |||
| − | |||
=== Vacuum boundary conditions === | === Vacuum boundary conditions === | ||
Vakuumi jnejne... | Vakuumi jnejne... | ||
| − | === | + | === Radially infinite, axially finite 3D geometry === |
| − | + | ||
| − | + | ||
Revision as of 14:22, 25 February 2016
Boundary conditions are invoked when the particle crosses the boundary from the defined part of the geometry into a region labeled as "outside" in the cell cards. The outcome then depends on the boundary conditions, as defined by the "set bc" option. Serpent provides three types of boundary conditions:
- Black boundary - the particle is killed
- Reflective boundary - the particle is reflected back into the geometry
- Periodic boundary - the particle is moved to the opposite side of the geometry
Reflective and periodic boundary conditions can be used to construct infinite and semi-infinite lattice structures. The way these boundary conditions are handled in Serpent is somewhat different from other Monte Carlo codes. Instead of stopping the neutron at the boundary surface, reflections and translations are handled by coordinate transformations. This limits the outermost boundary to a few specific surface types that form regular lattices. In 2D geometries such surfaces are:
- Square prism ("sqc") - forms a 2D square lattice
- Hexagonal prisms ("hexxc" and "hexxyc") -- form 2D hexagonal lattices
- Rectangular prism ("rect") - forms a 2D rectangular lattice
And in 3D:
- Cube ("cube") - forms a 3D cubical lattice
- Cuboid ("cuboid") - forms a 3D cuboidal lattice
- Truncated hexagonal prisms ("hexxprism" and "hexyprism") - form a 3D hexagonal lattices
Repeated boundary conditions are invoked only on the first surface listed in the "outside" type cells. Since the geometry boundary may consist of additional surfaces, some boundaries may be treated as reflective or periodic, while others are treated as vacuum. In reactor geometries there are typically three possible configurations:
- Infinite 2D geometry
- The geometry has no dependence on the z-coordinate. The outer boundary is defined by one of the 2D surfaces listed above.
- Radially infinite, axially finite 3D geometry
- The outer boundary is defined by one of the 2D surfaces listed above and two axial planes ("pz"). The boundary condition takes effect in the radial direction only, while the axial boundaries are vacuum.
- Infinite 3D geometry
- The outer boundary is defined by one of the 2D surfaces listed above. The boundary condition takes effect in all directions.
These configurations are demonstrated below.
Infinite 2D geometries
Vacuum boundary conditions ("set bc 1"). See animated particle tracks.
Reflective boundary conditions ("set bc 2"). See animated particle tracks.
Periodic boundary conditions ("set bc 3"). See animated particle tracks.
Vacuum boundary conditions
Vakuumi jnejne...