Delta- and surface-tracking
This a brief description on the delta-tracking based transport routine used in Serpent. The method is also used by other Monte Carlo codes, most notably in the HOLE geometry package in MONK and MCBEND. The original delta-tracking algorithm was introduced by Woodcock in 1965,[1] and a mathematical verification was derived by Coleman in 1968.[2] Delta-tracking is well described in a text book by Lux and Koblinger,[3] and a description of the methodology used in Serpent is found in an article in Annals of Nuclear Energy from 2010.[4]
The input parameters related to delta-tracking are:
- set dt - sets the probability threshold used for selecting between surface- and delta-tracking
- set forcedt - enforces the use of delta-tracking in a given list of materials
- set blockdt - enforces the use of surface-tracking in a given list of materials
- set minxs - definse the mean-free-path of collisions used to score the collision flux estimator
The output parameters are:
- TODO
Contents
Transport algorithm in Monte Carlo simulation
The Monte Carlo simulation consists of a large number particle histories, in which the random walk of an individual particle is followed, or tracked, through the geometry from its birth to eventual absorption or escape. Tracking is most typically carried out in a constructive solid geometry (CSG), composed of homogeneous material cells, which are defined by combinations of elementary and derived surface types. Serpent 2 also has two advanced geometry types, based on STL format CAD models and an unstructured polyhedral mesh.
The transport simulation follows a random walk from one interaction to the next. The procedure can be described as follows:
- Sample path length (distance to next collision)
- Transport neutron to the collision point
- Sample interaction
If the sampled interaction is scattering, the procedure restarts from beginning by sampling the distance to the next collision. The direction and energy are changed in each scattering event.
By definition, the interaction probability per traveled path length is given by the macroscopic total
cross section (denoted here as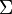 
). If it is assumed that the particle travels through an infinite
homogeneous medium characterized by constant total cross section, it can be shown that the free path length follows an exponential distribution. This distribution can be sampled using the inverse method, and the distance to the next collision site is given by:
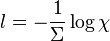where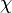 
is a uniformly distributed random variable on the unit interval.
The prerequisite of using this simple formula for sampling the distance to the next collision site is that the material is infinite and homogeneous. If this is not the case, the integral in (37) does not hold, and the sampled path length is not statistically valid.
Surface- and delta-tracking
The fact that the particle may cross the boundary between two material regions means that the interaction probability changes along the sampled path. This must be taken into account by stopping the track at the boundary crossing and sampling a new path length according to the new interaction probability.
Hybrid method used in Serpent
Advantages and limitations
References
- ^ Woodcock, E. R., Murphy, T., Hemmings, P. J., and Longworth, T. C. "Techniques used in the GEM code for Monte Carlo neutronics calculations in reactors and other systems of complex geometry." ANL-7050, Argonne National Laboratory, 1965.
- ^ Coleman, W. A. "Mathematical verification of a certain Monte Carlo sampling technique and applications of the technique to radiation transport problems." Nucl. Sci. Eng., 31 (1968) 76–81.
- ^ Lux, I. and Koblinger, L. "Monte Carlo Particle Transport Methods: Neutron and Photon Calculations." CRC Press, Inc. (1991).
- ^ Leppänen, J. "Performance of Woodcock delta-tracking in lattice physics applications using the Serpent Monte Carlo reactor physics burnup calculation code." Ann. Nucl. Energy 37 (2010) 715–722.
